A Thought Experiment

Saturday, May 13, 2017

VOLUME 0: ELEVATIONAL Table of Contents

Long term deployment
of space borne enterprises

require reliable raising to orbit
of Earth bound resources

without risky rockets.

Volume 0: ELEVATIONAL
1.	NEED TO ELEVATE. Humanity's space presence will require frequent, reliable elevation of Earth resources into orbit. BACKGROUND: Traditional Space Elevator's "tether" concept could be a start.
2.	UP-LINK TETHER: Climbers Ascend Tether *to GEO* Node.** Associated "strain" might break even the strongest cable at anytime. Thus, a physical cable requires an instant backup capability.
3.	DOWN-LINK: Climbers Descend Tether to Marine Anchor. During normal ops, dedicated downlink tether would provide downward bound service for climbers to return to Earth.
4.	OUT-LINK TETHER: Beyond GEO to Apex Anchor. (AA) . Thought Experiment (TE) considers innovative ways to leverage Space Elevator (SE) beyond Geosynchronous Equatorial Orbit (GEO).
5.	LIFEBOATS: Ride the Virtual Tether. For a reliable, rapid return to Earth's surface, ride the virtual tether, an Earth based, high speed, particle beam to enable "lifeboats" to land at zero velocity.
6.	BASE STATION: Forget Down-Link's physical tether; instead, exclusively use lifeboats to travel Down-Link Virtual Tether back to Base Station with a reliable particle beam capability.
7.	SEVERED TETHER: Some scenarios end badly. EXAMPLES: 1) Taut tether might "snap" and recoil. 2) A broken tether might wrap around the Earth. 3) ... perhaps even a "ring of fire" around the globe.
8.	ELEVATIONAL ALTERNATIVES Besides the Space Elevator (SE), there are several other non-rocket proposals which might lift a vehicle and payload from Earth's surface to Earth's orbit.
9.	BEAM ME UP! Thought Experiment (TE) proposes another non-rocket method to reach GEO. Replace Up-Link's physical tether with a virtual tether, a beam of ions from Base Station.
10.	HIGH STAGE ONE: Leverage Lofstrom's Launch Loop concept to avoid wind and weather in lower atmosphere and get a head start on trip to GEO.
11.	CONSTRUCTING SPACE ELEVATOR. Using physical tether to construct subsequent tethers might make sense. HOWEVER, virtual tether makes more sense; no rocket risk nor risk of sever.
12.	SPACE TUG: Earth Orbits. TE's Space Tug could move vehicles between tethers; but it would be best used in moving Space Habitats among different terrestrial orbits. Also, see "Ion Thrusters" and "Specific Impulse".
13.	BASE OFF EQUATOR? Can a tether anchor off the Equator?? Not much. HOWEVER, a Base Station can locate well away from equator and still project an ion beam toward the *GEO* Node.
14.	ELEVATIONAL CHALLENGES MAIN CHALLENGE: Quickly move pax/cargo from Earth's Equator to *GEO* without the absurdly long cable (might extend 1/4 distance to the Moon!!!!).
15.	BEAM ME OUT!!! Expand range of orbital destinations from strictly GEO to well beyond. Even escape Earth's gravity to travel throughout the Solar System.

VOLUME 0: ELEVATIONAL
VOLUME I: ASTEROIDAL
VOLUME II: INTERPLANETARY
VOLUME III: INTERSTELLAR

Saturday, August 30, 2014

VOLUME I: ASTEROIDAL Table of Contents

Over the next century,

mankind's dwellings will include habitats

throughout the Solar System.

HABITATS: Some human colonies will live in large, spinning cylinders constructed from "in situ" material from asteroids and comets.
EARTH LIKE GRAVITY: Spinning cylinders will simulate g-force via centrifugal force along longitudinal axis.
ENERGY SOURCE: Large, adjacent mirrors will reflect sunlight into habitats for plentiful energy.
FRESH FOOD: Essential ingredients from Mother Earth will enable robust agricultures.
SPENDING MONEY: Harvesting of space bound materials will enable a robust economy among the many habitats as well as Mother Earth
POPULATIONS: Smaller habitats will easily house 10,000 people; larger habitats will provide comfortable quarters for well over 100,000.

Volume I: ASTEROIDAL
1.	HABITATS CAN ORBIT. Transform selected asteroids into orbiting habitats; i.e., "orbiters". Compare orbits. NOTE: Background material: Orbit Elements, Inclination, and Omega, Orbit "Rolls"
2.	HABITATS CAN TRANSPORT. As transporters, habitats can move large human populations throughout the Solar System; for example, to Mars orbit via a simple "semi-orbit", described in an associated TABLE.
3.	HABITATS CAN CYCLE BACK TO EARTH. Refashion selected Near Earth Asteroids (NEAs) as resonant cyclers which rendezvous with Earth every 2 years. See two associated tables: I and II.
4.	HABITATS CAN CYCLE TO MARS: TE coins term "Marsonance"; design Habitat's orbit to routinely rendezvous with Mars due to well designed orbital "resonance". (See TABLE.)
5.	HABITATS CAN IMPORT RESOURCES FROM EARTH. To properly provision initial habitats, use "space elevator" to export many materials from Mother Earth to her children.
6.	HABITATS CAN TERRAFORM. For Earth-like environment, habitat transform processes include: 1) import Earth soil for both minerals and microbes; 2) spin for gravity; 3) mirrors reflect sunlight for energy, etc.
7.	HABITATS CAN COMMUNICATE: Refashioned habitats can communicate all through the Solar System by deploying specialized comm capsules.
8.	SPACE TUG: Solar Orbits. TE's Space Tug could help Space Habitats transition to different orbits around the Sun. Also, see "Ion Thrusters" and "Specific Impulse".
9.	NEW MOON: LAUNCHING ALPHA. (Leverage New Moon for a slightly smaller, slightly quicker Solar orbit.) Alpha could be a huge habitat, 60° ahead of Earth. To build such a habitat, use Luna as a launch platform. See Alpha Launch Tables.
10.	FULL MOON AND BEYOND: LAUNCH OMEGA. (Leverage Full Moon for a slightly larger, slightly slower orbit around Sol.) Omega could be a huge habitat at Lagrange Point 5 (L5), 60° behind Earth. At 1 AU from Earth. See Omega Launch Tables
11.	EARTH's ELLIPTICITY Helps a Lot!!! Earth's orbit is near circular, but it still has enough "eccentricity" for a habitat to more quickly attain a parking sport of 60° from Earth.
12.	LEVERAGING LAMBDA for Cyclers. Synergize Habitats Alpha and Omega with 2 year cycler orbits for enormous benefits. Requires careful placement of lambda, semi-latis rectum. See 2 YEAR CYCLER TABLE.
13.	HABITATS CAN MINE MINERALS from the Asteroid Belt, a plentiful source of materials required to construct and maintain habitats in space.
14.	HABITATS CAN EXTRACT ELEMENTS from the Gas Giants, a plentiful source of essential elements required to power habitats in deep space beyond the reach of effective sunlight.
15.	HABITATS CAN MIGRATE Initial habitats will orbit and cycle, but g-force propulsion will enable much quicker migration to the planets in days and to nearby stars in years.

VOLUME O: ELEVATIONAL
VOLUME I: ASTEROIDAL
VOLUME II: INTERPLANETARY
VOLUME III: INTERSTELLAR

VOLUME II: INTERPLANETARY Table of Contents

Interplanetary flights will become routine
(much like airline travel today)
because travel time will become reasonable.

Furthermore, spacecraft will maintain comfortable Earthlike conditions (gravity, atmosphere, comfortable billets, entertainment, etc) throughout the flight.
Consider Einstein's thought experiment about an accelerating elevator. If the elevator accelerates at same rate as free falling objects near Earth's surface, then occupants will feel same g-force as if they're static on Earth's surface. (Einstein called this "equivalence".)
Instead of Einstein's elevator, our thought experiment notionalizes a high performance spaceship to accelerate at rate, g, to produce gravity like force (g-force). A g-force trip to nearby planets will take days or weeks (orbiting vehicles now take years). We speculate that g-force propulsion can be accomplished with well known science and slight advances in current technology.

Volume II: INTERPLANETARY
1.	ACCELERATE FOR A DAY: Consider Einstein's famous "Thought Experiment" which states an equivalence between being static on Earth's surface or accelerating at 1 g through space.
2.	ACCELERATE TO THE PLANETS: in days; G-force acceleration greatly increases ship's velocity. However, the ship must SLOWDOWN throughout the second half of the flight.
3.	MOMENTUM MAKES IT HAPPEN: High speed exhaust particles approach light speed; thus, their relativistic mass gain further increases momentum to further enhance propulsion.
4.	MASS TO MOTION: On board particle accelerators can drive exhaust particles with enormous momentum to drive spaceships. Express fuel consumption as % initial gross weight per day.
5.	PUSH PARTICLES TO INTERPLANETARY. Particle exhaust speeds from .1c to .5c will transport people, cargo and habitats to nearby planets inside the Kuiper Belt (KB).
6.	BEST OF BREED ION DRIVE: VASIMR. Prime example of current "Ion Thruster", technology is Dr. Chang-Diaz's Variable Specific Impulse Magneto-plasma Rocket (VASIMR).
7.	PROFILE TO THE PLANETS: G-force can propel vessel in straight line to destination. However, flight profile must be carefully planned and executed.
8.	G-FORCE TO MARS: Water can get us to our red neighbor quickly. Thought experiment assumes water as the source of plasma particles for the propulsion system of the g-force spaceship.
9.	FINITE FUEL: Consider "g-force" propulsion, specified quantity of charged particles exit aft at near light speeds. At a given consumption rate, logarithms can approximate vessel's range.
10.	ACCELERATORS IN SPACE: Let particle accelerators propel g-force vessels.
11.	G-FORCE ELEVATORS: BEAM ME UP quickly move pax/cargo from Earth's Equator to Geographic Equatorial Orbit (GEO) Node without the absurdly long tether.
12.	TO URANUS.. Why go?? Helium-3, an isotope of Helium, can produce cheaper, cleaner fuel for onboard power needs for space faring enterprises. He-3 is plentiful on the Gas Giants; with the lowest escape velocity, mining HE-3 from Uranus might prove fruitful.
13.	KEEPERS FROM KUIPER Space communities will eventually depend on raw materials from space. Kuiper Belt has plenty.
14.	SUPER G-FORCE Can interplanetary cargo travel quicker than passengers at g-force? YES!!!! Less time requires more fuel, but it may be worth it.
15.	EXTRAPLANETARY: Prep for the Stars. Transition to interstellar. Eventually, interplanetary flights will become routine. When they do, the practicality of interstellar flights will become imminent.

VOLUME 0: ELEVATIONAL
VOLUME I: ASTEROIDAL
VOLUME II: INTERPLANETARY
VOLUME III: INTERSTELLAR

Thursday, August 28, 2014

VOLUME III: INTERSTELLAR Table of Contents

With traditional propulsion,
flight to nearby stars take long centuries.
FORTUNATELY, g-force reduces flight time to a few years.

Unfortunately, fuel can severely limit duration/distance for interstellar g-force voyages; though, fuel is not a problem for interplanetary flights. G-force vessels can easily carry sufficient fuel to accelerate at constant g-force throughout a trip to Mars, which would take a few days and only a few percent of the ship's mass for fuel. However, interstellar vessels would easily consume well over 100% of its weight in fuel during the multi-year voyage.

Thus, interstellar g-force ships will conduct their voyages via

three phases:

PHASE I. Accelerate at g-force for about a year to a significant percentage of light speed.
PHASE II. Cruise for a few years at this speed to save fuel (simulate gravity via longitudinal spin).
PHASE III. Decelerate at g-force back to near zero velocity for orbital operations at the destination stellar system.

Volume III: INTERSTELLAR
1.	INTERSTELLAR SCENARIOS Thought Experiment (TE) has grouped some common scenarios as: 1) Theoretical 2) Feasible 3) Practical. Subsequent chapters focus on the practical.
2.	PUSH TOWARD INTERSTELLAR. Interplanetary performance envelope will need considerable "pushing" for interstellar flights. Particle exhaust speeds must be at least 86.6% light speed (.866 c).
3.	ACCELERATE FOR A YEAR: Compare spaceship's g-force speeds with c, light speed. See associated 1G TABLE: Accelerate for 1 Year.
4.	DETERMINE DUE DISTANCE. Use exponential to determine g-force interstellar speeds; from integral calculus, use integral to determine distance duly traveled.
5.	TO NEIGHBOR STARS: Between an initial, year long, g-force acceleration and the voyage's final year of g-force deceleration, interstellar flights need a multi-year cruise phase to conserve fuel.
6.	PRACTICALITY: LIMITED RANGE G-force acceleration requires mass/energy conversion. Since spaceship has limited mass; it has limited range. Inevitable inefficiencies limit range even further.
7.	DYNAMIC EFFICIENCY FACTOR: Make the feasible range more practical with a dynamic efficiency factor which inversely correlates with vessel performance (particle velocity as it exits vessel's exhaust).
8.	FUSION WILL WARM US. Fusion reactors will probably provide the power (though not the propulsion) for humans to live well and prosper during multi-year journeys to the stars.
9.	INTERSTELLAR SUPER G. Unmanned AI vessels might use greater than g-force propulsion to resupply manned, interstellar vessels between the stars. See associated 7G TABLE: Accelerate for 100 Days.
10.	SNOWBALL FROM OORT From Oort's many comets, construct ice encased vessels to travel at interstellar super G throughout our stellar neighborhood. See associated 7G TABLE: Decelerate for 48¼ days.
11.	ANNUAL SNOWBALLS Interstellar travelers might need multiple resupplies throughout their voyage. Thus, TE proposes more ways to throw more snowballs. See associated 1G TABLE: Decelerate for 1 Year.
12.	ENHANCED TIME DILATION. With annual snowballs, g-force vessels could conceivably accelerate to 86.6%c; then, passengers would age ½ as fast as Earth observers. (NOTE: Without "snowballs," practical cruise speed is 64.4%c; thus, STANDARD TIME DILATION TO AC:.)
13.	INTERSTELLAR COMMUNICATIONS Maintaining huge data flows over extreme distances will likely involve well planned placement of AI controlled, interstellar beacons. IMPORTANT, these necessary, autonomous devices must actively avoid collisions, especially with the very vessels they support.
14.	INTERSTELLAR LIGHTHOUSES Like Earth's coastal lighthouses, neighboring stars can help us avoid enroute hazards. Singularities (aka "Black Holes") are especially insidious.
15.	HUBS: Sol's closest stellar neighbors can help humanity travel to even further stars. Vessels can stop there to replenish resources before traveling on. To better understand "hub" concept, also consider following. OCTANTS: TE groups neighboring stellar systems (perhaps 51 within 15 LYs) into 8 octants. BEARINGS can help vessels precisely track distance along the course line.

VOLUME 0: ELEVATIONAL
VOLUME I: ASTEROIDAL
VOLUME II: INTERPLANETARY
VOLUME III: INTERSTELLAR

Sunday, July 20, 2014

7G TABLE: Decelerate for 48 ¼ Days

VOLUME 0: ELEVATIONAL
VOLUME I: ASTEROIDAL
VOLUME II: INTERPLANETARY
VOLUME III: INTERSTELLAR

To effectively accomplish an interstellar resupply mission, an Artificial Intelligent (AI) vessel could use 7G propulsion to quickly intercept the primary 1G vessel. However, the 7G vessel must slow down prior to intercept in order to match the 1G vessel cruise velocity. This table describes daily progress throughout the deceleration duration.

7G Deceleration for 48 ¼ Days

Previous table, 7G Acceleration for 100 Days, describes daily progress of vessel accelerating from zero velocity at 7g.

After 100 days of 7g acceleration, a vessel travels total distance of 9,842 AUs (.155 Light Year, LY). It gained velocity of about 150 AU/day (.866 c, 86.6% light speed).

Assume 7G vessel cruises at this velocity until the optimal time/distance to start decelerating at 7g.

Decel.
Time(t)

Spot
Velocity (V_t)

Spot
Distance (d_t)

Daily
Dist. (d_Δ)

7G
Dist.(d_7G)

Total
Fuel (F)

0 days

149.93 AU/dy

86.59% c

9,811.1 AU

0.1551 LY

0.0 AU

9,811.1 AU

27.974% GW₀

1 days

149.46 AU/dy

86.32% c

9,661.7 AU

0.1528 LY

149.4 AU

9,960.5 AU

28.210% GW₀

2 days

148.98 AU/dy

86.04% c

9,512.8 AU

0.1504 LY

148.9 AU

10,109.4 AU

28.445% GW₀

3 days

148.48 AU/dy

85.76% c

9,364.4 AU

0.1481 LY

148.4 AU

10,257.9 AU

28.679% GW₀

4 days

147.98 AU/dy

85.46% c

9,216.5 AU

0.1457 LY

147.9 AU

10,405.8 AU

28.913% GW₀

5 days

147.46 AU/dy

85.17% c

9,069.1 AU

0.1434 LY

147.4 AU

10,553.2 AU

29.146% GW₀

6 days

146.94 AU/dy

84.86% c

8,922.2 AU

0.1411 LY

146.9 AU

10,700.1 AU

29.378% GW₀

Given

(1 - (1-Δ)^100-t) × c

c×(100-t)+	V_t ln(1-Δ)

d_t-1 - d_t

d_Δ + Σd_Δ

1-(1-ε∇)^100+t

For success, the 7G resupply vessel must slow down to match the 1G vessel's cruise velocity (.644c = 111.5 AU/day). This table describes daily progress throughout the 48¼ days of 7G deceleration.

Interstellar 1G Vessel

starts its one year of acceleration at day 0.

After this year, vessel stops acceleration and cruises at 111.5 Astronomical Units per day (.644 c).

One year of 1G acceleration has taken vessel to 23,841 AUs, .377 Light Year (LY).

Interstellar 7G Snowball

In this example, 7G snowball (traditional habitat encased in large volume of ice) starts its 100 day acceleration at day 260 of 1G vessel’s acceleration.

On day 360, 7G vessel stops propulsion, and cruises at 149.9 AUs per day (.865c).

100 days of 7G acceleration takes vessel to 9,842 AU, (= .155 LY).

Decel.
Time(t)

Spot
Velocity (V_t)

Spot
Distance (d_t)

Daily
Dist. (d_Δ)

7G
Dist.(d_7G)

Total
Fuel (F)

7 days

146.40 AU/dy

84.56% c

8,775.8 AU

0.1388 LY

146.4 AU

10,846.5 AU

29.609% GW₀

8 days

145.86 AU/dy

84.24% c

8,630.0 AU

0.1365 LY

145.8 AU

10,992.3 AU

29.840% GW₀

9 days

145.30 AU/dy

83.92% c

8,484.7 AU

0.1342 LY

145.3 AU

11,137.6 AU

30.070% GW₀

10 days

144.73 AU/dy

83.59% c

8,340.0 AU

0.1319 LY

144.7 AU

11,282.3 AU

30.299% GW₀

11 days

144.15 AU/dy

83.26% c

8,195.8 AU

0.1296 LY

144.1 AU

11,426.4 AU

30.527% GW₀

12 days

143.56 AU/dy

82.91% c

8,052.3 AU

0.1273 LY

143.6 AU

11,570.0 AU

30.755% GW₀

Given

(1 - (1-Δ)^100-t) × c

c×(100-t)+	V_t ln(1-Δ)

d_t-1 - d_t

d_Δ + Σd_Δ

1-(1-ε∇)^100+t

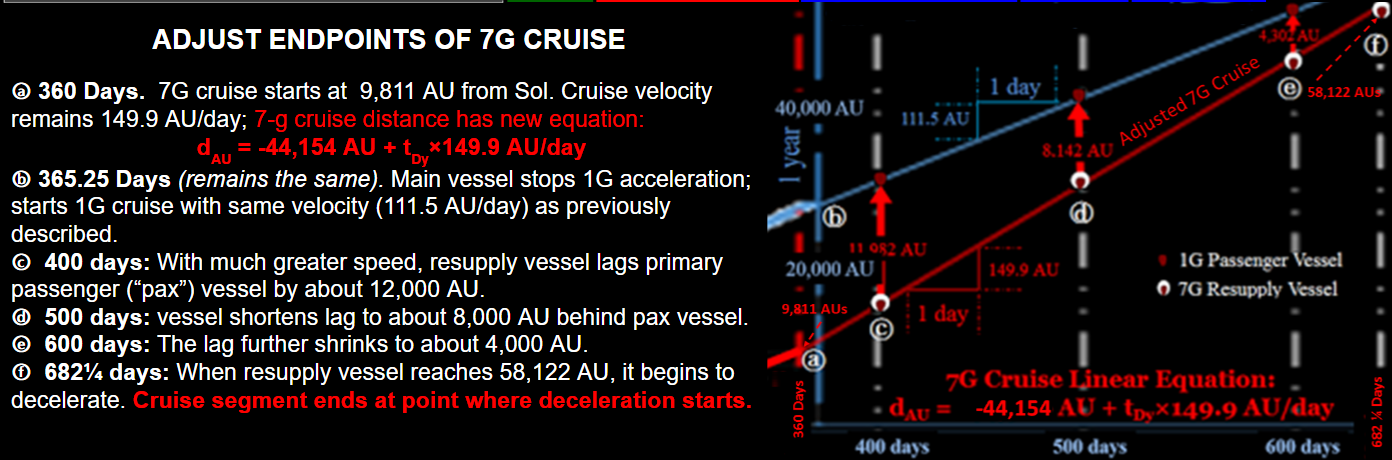
Points ⓐ thru ⓕ map out following events:

ⓐ After 360 days, resupply vessel ends 100 days of 7G propulsion and starts cruise at 149.9 AU/day.

ⓑ After 365¼ days of 1G acceleration, primary vessel cruises at 111.5 AU/day.

ⓓ After 500 days (about 135 days of constant velocity),, resupply vessel closes the gap to slightly over 8,000 AU.

ⓔ 600 days (100 more days of constant velocity), gap closes even more to just over 4,000 AU.

ⓕ 684 days, gap shrinks to about 1,000 AU in prep for 7G vessel’s deceleration duration of 48¼ days needed to match speed of primary vessel.

Describe primary vessel’s cruise distance by linear equation:

d = 111.5 t - 16,884 AU

Resupply vessel’s cruise distance:

d= 149.9 t - 44,152 AU

By inspection, we expect a pending intercept of these two cruise tracks about one LY and two years from start of primary vessel’s track. HOWEVER, the resupply vessel track must become nonlinear at about 684 days for 48¼ day deceleration maneuver.

Decel.
Time(t)

Spot
Velocity (V_t)

Spot
Distance (d_t)

Daily
Dist. (d_Δ)

7G
Dist.(d_7G)

Total
Fuel (F)

13 days

142.96 AU/dy

82.57% c

7,909.3 AU

0.1251 LY

143.0 AU

11,712.9 AU

30.982% GW₀

14 days

142.34 AU/dy

82.21% c

7,767.0 AU

0.1228 LY

142.3 AU

11,855.3 AU

31.208% GW₀

15 days

141.72 AU/dy

81.85% c

7,625.3 AU

0.1206 LY

141.7 AU

11,997.0 AU

31.433% GW₀

16 days

141.08 AU/dy

81.48% c

7,484.2 AU

0.1183 LY

141.1 AU

12,138.1 AU

31.658% GW₀

17 days

140.42 AU/dy

81.10% c

7,343.7 AU

0.1161 LY

140.4 AU

12,278.6 AU

31.881% GW₀

18 days

139.76 AU/dy

80.72% c

7,203.9 AU

0.1139 LY

139.8 AU

12,418.3 AU

32.105% GW₀

Given

(1 - (1-Δ)^100-t) × c

c×(100-t)+	V_t ln(1-Δ)

d_t-1 - d_t

d_Δ + Σd_Δ

1-(1-ε∇)^100+t

Decel.
Time(t)

Spot
Velocity (V_t)

Spot
Distance (d_t)

Daily
Dist. (d_Δ)

7G
Dist.(d_7G)

Total
Fuel (F)

19 days

139.08 AU/dy

80.32% c

7,064.8 AU

0.1117 LY

139.1 AU

12,557.5 AU

32.327% GW₀

20 days

138.38 AU/dy

79.92% c

6,926.4 AU

0.1095 LY

138.4 AU

12,695.9 AU

32.549% GW₀

21 days

137.67 AU/dy

79.51% c

6,788.7 AU

0.1073 LY

137.7 AU

12,833.6 AU

32.770% GW₀

22 days

136.95 AU/dy

79.10% c

6,651.7 AU

0.1052 LY

137.0 AU

12,970.6 AU

32.990% GW₀

23 days

136.21 AU/dy

78.67% c

6,515.4 AU

0.1030 LY

136.3 AU

13,106.9 AU

33.210% GW₀

24 days

135.46 AU/dy

78.24% c

6,379.9 AU

0.1009 LY

135.5 AU

13,242.4 AU

33.428% GW₀

Given

(1 - (1-Δ)^100-t) × c

c×(100-t)+	V_t ln(1-Δ)

d_t-1 - d_t

d_Δ + Σd_Δ

1-(1-ε∇)^100+t

After 684 days of mission time, resupply vessel flight profile used 7G acceleration and high speed cruise to reach a position 58,340 AU from Sol.
At this point, 7G vessel is only 1,076 AU behind the 1G vessel.
The 7G vessel must start the 48¼ days of 7G deceleration required to slow down from 149.9 AU/day to 111.5 AU/day, cruise velocity of the primary vessel.

For functional rendezvous, both the primary mission vessel and the resupply vessel must match velocities at the same position at the same time.

In this example, both vessels simultaneously reach 64,796 AU (about one LY) along the track from Sol to neighboring star.

Determine Intersection Point

Assume the 1G pax vessel accelerates at 1G for one year; then, cruises at constant velocity. Thus, determine distance traveled per following linear equation:

d_1G = -.267 LY + .644 c × t

Assume resupply vessel starts 7G accelerates at 265.25 days after mission vessels begins. 100 days later (365.25 days into mission), 7G vessels stops acceleration and starts cruise. Thus, determine total distance traveled via following linear equation:

d7G = -.711 LY + .866 c × t

To determine intersection point of the two linear equations, set them equal as shown:

d1G = -.267 LY + .644c × t = -.711 LY + .866c × t = d7G

For convenience, substitute following terms: LY = 63,241 AU and c = 173.15 AU/day:

-16,885 AU + 111.5 AU/day × t = -44,964 AU + 149.9 AU/day × t

thus, solve for: tInt = 731.2 days and dInt= 64,644 AUs.

These linear equations enable us to determine that the two cruising vessels will meet at time equals 731.2 days (2 years) since day zero and distance equals 64,644 AU (about 1 LY) from 1G pax vessel's starting point. However, the two vessels cannot gracefully rendezvous because they still have a huge velocity differential of about .22 c. A following section proposes a deceleration method to synchronize velocity in addition to time and distance.

Decel.
Time(t)

Spot
Velocity (V_t)

Spot
Distance (d_t)

Daily
Dist. (d_Δ)

7G
Dist.(d_7G)

Total
Fuel (F)

25 days

134.70 AU/dy

77.79% c

6,245.1 AU

0.0988 LY

134.8 AU

13,377.2 AU

33.646% GW₀

26 days

133.91 AU/dy

77.34% c

6,111.1 AU

0.0966 LY

134.0 AU

13,511.2 AU

33.864% GW₀

27 days

133.12 AU/dy

76.88% c

5,977.9 AU

0.0945 LY

133.2 AU

13,644.4 AU

34.080% GW₀

28 days

132.30 AU/dy

76.41% c

5,845.5 AU

0.0924 LY

132.4 AU

13,776.8 AU

34.296% GW₀

29 days

131.47 AU/dy

75.93% c

5,713.9 AU

0.0904 LY

131.6 AU

13,908.4 AU

34.512% GW₀

30 days

130.62 AU/dy

75.44% c

5,583.1 AU

0.0883 LY

130.7 AU

14,039.1 AU

34.726% GW₀

Given

(1 - (1-Δ)^100-t) × c

c×(100-t)+	V_t ln(1-Δ)

d_t-1 - d_t

d_Δ + Σd_Δ

1-(1-ε∇)^100+t

Decel.
Time(t)

Spot
Velocity (V_t)

Spot
Distance (d_t)

Daily
Dist. (d_Δ)

7G
Dist.(d_7G)

Total
Fuel (F)

31 days

129.76 AU/dy

74.94% c

5,453.2 AU

0.0862 LY

129.9 AU

14,169.0 AU

34.940% GW₀

32 days

128.88 AU/dy

74.43% c

5,324.2 AU

0.0842 LY

129.0 AU

14,298.1 AU

35.153% GW₀

33 days

127.98 AU/dy

73.91% c

5,196.1 AU

0.0822 LY

128.1 AU

14,426.2 AU

35.366% GW₀

34 days

127.06 AU/dy

73.38% c

5,068.9 AU

0.0802 LY

127.2 AU

14,553.4 AU

35.577% GW₀

35 days

126.13 AU/dy

72.84% c

4,942.6 AU

0.0782 LY

126.3 AU

14,679.7 AU

35.788% GW₀

36 days

125.17 AU/dy

72.29% c

4,817.3 AU

0.0762 LY

125.3 AU

14,805.0 AU

35.999% GW₀

Given

(1 - (1-Δ)^100-t) × c

c×(100-t)+	V_t ln(1-Δ)

d_t-1 - d_t

d_Δ + Σd_Δ

1-(1-ε∇)^100+t

Decel.
Time(t)

Spot
Velocity (V_t)

Spot
Distance (d_t)

Daily
Dist. (d_Δ)

7G
Dist.(d_7G)

Total
Fuel (F)

37 days

124.20 AU/dy

71.73% c

4,692.9 AU

0.0742 LY

124.4 AU

14,929.4 AU

36.208% GW₀

38 days

123.20 AU/dy

71.15% c

4,569.5 AU

0.0723 LY

123.4 AU

15,052.8 AU

36.417% GW₀

39 days

122.19 AU/dy

70.57% c

4,447.1 AU

0.0703 LY

122.4 AU

15,175.2 AU

36.626% GW₀

40 days

121.15 AU/dy

69.97% c

4,325.7 AU

0.0684 LY

121.4 AU

15,296.6 AU

36.833% GW₀

41 days

120.10 AU/dy

69.36% c

4,205.4 AU

0.0665 LY

120.3 AU

15,416.9 AU

37.040% GW₀

42 days

119.02 AU/dy

68.74% c

4,086.1 AU

0.0646 LY

119.3 AU

15,536.1 AU

37.246% GW₀

Given

(1 - (1-Δ)^100-t) × c

c×(100-t)+	V_t ln(1-Δ)

d_t-1 - d_t

d_Δ + Σd_Δ

1-(1-ε∇)^100+t

Decel.
Time(t)

Spot
Velocity (V_t)

Spot
Distance (d_t)

Daily
Dist. (d_Δ)

7G
Dist.(d_7G)

Total
Fuel (F)

43 days

117.92 AU/dy

68.11% c

3,968.0 AU

0.0627 LY

118.2 AU

15,654.3 AU

37.452%GW₀

44 days

116.80 AU/dy

67.46% c

3,850.9 AU

0.0609LY

117.1 AU

15,771.4 AU

37.657%GW₀

45 days

115.66 AU/dy

66.80%c

3,735.0 AU

0.0591 LY

115.9 AU

15,887.3 AU

37.861%GW₀

46 days

114.49 AU/dy

66.12% c

3,620.2 AU

0.0572 LY

114.8 AU

16,002.1 AU

38.065%GW₀

47 days

113.30 AU/dy

65.44% c

3,506.6 AU

0.0554 LY

113.6 AU

16,115.7 AU

38.268%GW₀

48 days

112.09 AU/dy

64.74% c

3,394.2 AU

0.0537 LY

112.4 AU

16,228.0AU

38.470%GW₀

Resupply Vessel Matches Cruise Velocity of Baseline "Pax" Vessel (1.0 yr of 1G Accel.)
at exactly the time/distance of the intercept.

48¼days

111.78 AU/dy

64.56% c

3,366.3 AU

0.0532 LY

27.9 AU

16,256.0 AU

38.520%GW₀

Given

(1 - (1-Δ)^100-t) × c

c×(100-t)+	V_t ln(1-Δ)

d_t-1 - d_t

d_Δ + Σd_Δ

1-(1-ε∇)^100+t

Decel.
Time(t)

Spot
Velocity (V_t)

Spot
Distance (d_t)

Daily
Dist. (d_Δ)

7G
Dist.(d_7G)

Total
Fuel (F)

52 days

106.98AU/dy

61.79%c

2,966.6 AU

0.2636LY

107.3AU

16,667.7AU

39.272%GW₀

53 days

105.64AU/dy

61.01%c

2,860.5AU

0.2652LY

106.0AU

16,773.7AU

39.471%GW₀

Resupply Vessel Matches Cruise Velocity of Slower "Pax" Vessel (0.9 yr of 1G Accel.)
at exactly the time/distance of the intercept.

53.4 days

105.10AU/dy

60.70%c

2,818.4AU

0.2659LY

42.0 AU

16,815.7AU

39.551%GW₀

54 days

104.27AU/dy

60.22%c

2,755.7AU

0.2662LY

62.6 AU

16,836.3AU

39.669%GW₀

Given

(1 - (1-Δ)^100-t) × c

c×(100-t)+	V_t ln(1-Δ)

d_t-1 - d_t

d_Δ + Σd_Δ

1-(1-ε∇)^100+t

VOLUME 0: ELEVATIONAL

VOLUME I: ASTEROIDAL

VOLUME II: INTERPLANETARY

VOLUME III: INTERSTELLAR

SLIDESHOW

A Thought Experiment

Saturday, May 13, 2017

VOLUME 0: ELEVATIONAL Table of Contents

Saturday, August 30, 2014

VOLUME I: ASTEROIDAL Table of Contents

VOLUME II: INTERPLANETARY Table of Contents

Thursday, August 28, 2014

VOLUME III: INTERSTELLAR Table of Contents

Sunday, July 20, 2014

7G TABLE: Decelerate for 48 ¼ Days

About Me

Links

Previous Posts