G-FORCE TO MARS

ContentsGetting ThereFlight Profile Range: 0.5 AUAccelerate to MidpointDecelerate to DestinationTotal Trip TimePropulsion SystemParticle SourceSome Cultural HistoryProfile Range: 1.0 AUSidereal vs. Synodic

---

---

---

Mars is the god of war, clothed in red, with his companions, Fear and Dread.

---

Getting There with Fuel

---

Thought experiment proposes "g-force" spacecraft with sufficient propulsion to increase its velocity 10 m/sec for every second of flight; thus, in flight speeds increase to 864 km per second for every day of g-force propulsion.

Equivalent Expressions of g

g	≈		10 m/sec sec	≈	864 km/sec day	≈	1,728 km/sec 2 days

As a result, in-flight travel times are greatly reduced compared to transfer orbits.  Current technology space vehicles take months to travel via transfer orbits from Earth to Mars. However, g-force flights to Mars will take only days.

---

EQUIVALENCE:  Crew and passengers enjoy Earth like gravity due to the constant push from the ship's continuous acceleration. In flight comfort is greatly increased.

---

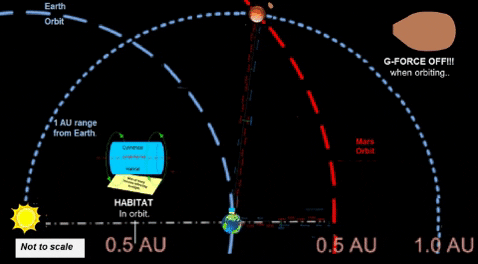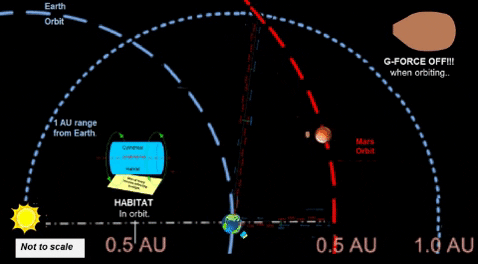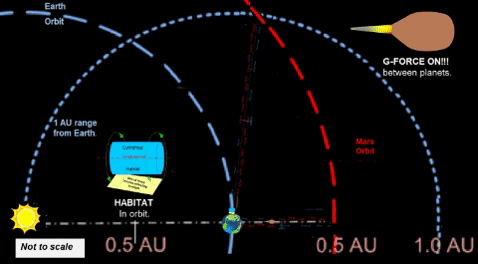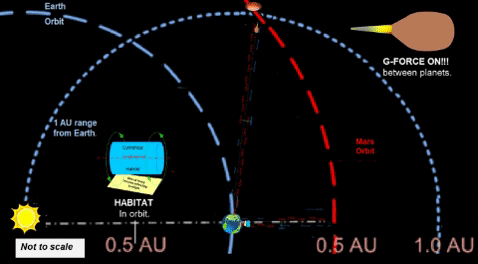
The quickest g-force flights will happen at the minimum distance. Earth-Mars opposition which brings the two planets to about 0.5 AU. Thus, thought experiment assumes 0.5 AU as minimum distance between Terra (aka "Earth") and Mars. Sidereal Period,T, is duration for an object to compute an entire orbit past a fixed celestial refercne, perhaps the  Line of Aries . This duration is regarded as the object's true orbital period. God's view from up North shows both planets rotating counter clockwise (CCW). Synodic Period, P, is the duration between successive oppositions. Most Earth bound mortals observe synodic periods. For example, Mars actually revolves around Sol at .524°/day (sidereal). However, Earth's sidereal rate is much faster (CCW at .999°/day). Thus, Earth bound observers see Mars revolving at the difference, ωΔ  = 0.475°/day, Mars's Synodic rate with respect to Earth. ωΔ = ωEarth - ωMars .475°/day = .999°/day - .524°/day P = 360°/ωΔ = 758 days About every 758 days, Synodic opposition brings Earth and Mars to about .5 AU apart. --Consider all Earth-Mars oppositions from Feb 22, 1901 to Sep 15, 2035. --Distances vary from .37 to .68 AU with an average of .55 AU.  --Intervals between successive oppositions range from 757 to 798 Earth days with an average of 769 days. Ref: The Planet Mars: A History of Observation and Discovery by William Sheehan; see Appx 1: Oppositions of Mars, 1901--2035

---

---

---

Accelerate to Midpoint

In this example, three tenths day (.3D = 2.4 hours) of g-force takes the vessel about .025 AU.  A complete day of g-force takes ship to .25 AU, half of the minimum distance between Earth and Mars. This occurs at Mars's opposition when Earth is directly between Sol and Mars (co-linear). As the flight progresses, acceleration takes the ship to ever greater velocities. Thus, above time and distance scales show that .1 day increments cover ever greater distance as time increases. Thus, first day of g-force acceleration brings ship to 864 km per second (compares to just 11 km/sec velocity to escape Earth's orbit). Let d be distance between departure and destination. Example:  At Mars opposition, distance (d) from Earth to Mars can be .5 AU. If vessel accelerates to midway (dMid = d/2); then, acceleration time, tAcc, is: Recall Newton's Motion Equations:  tAcc = √(2×dMid/g) Which can be restated:  tAcc= √(d/g) Recall g (10 m/sec2) can be restated as .5AU/day2: tAcc= √(.5 AU/(.5AU/day2)) = 1 day

Decelerate to Destination

Propulsion System

Thought experiment assumes propulsion system with on-board particle accelerator capable of outputting constant, consistent stream of high speed H₂O ions (water super-heated to plasma particles). For discussion's sake, Thought Experiment (TE) assumes that 1% of ship's weight transformed into high speed, exhaust particles could enable our space vessel to maintain g-force for one day. TE subsequently assumes g-force travel to/from a .5 AU destination would require 4 days and about 4% of ship's GW.

Four percent of a vessel's Take Off Gross Weight (4%TOGW) is an enormous amount of mass. Assume interplanetary vessel is the size of an aircraft carrier, about 300,000 metric Tonnes (mTs). Thus, our g-force propulsion system would require:

• 12,000 metric Tonnes of water for the trip.
• 3 million kilograms of water per day (an Olympic swimming pool holds about this much).
• 34.72 kilograms of water per second (a large Jacuzzi holds about this much).

In contrast, a typical contemporary, ion drive provides much less propulsion than TE's proposed G-force vessel. Current ion-drive vessels might use about (100 grams) of xenon per day, a much smaller amount of a substance much less available than H₂O.

Particle Source

Thought experiment assumes water as the source of plasma particles for the propulsion system of the g-force spaceship. For the near future, water supplies will likely be restricted to an occasional comet which passes our way. In a more distant future, we can travel to extraterrestial sources of water: Near Earth Objects (NEOs), asteroid belt, Kuiper Belt, Oort Cloud and harvest water at will. In today's environment, the only sure source of water is the oceans of Earth, and exporting huge quantities of water from Earth's surface into near space will be challenging and probably not even desirable.

To maintain g-force throughout powered flight, TE proposes particle accelerator propulsion which transforms large quantity of water into plasma ions and accelerates them to very high speeds (perhaps 27%c) and discharges them from exhaust for very high momentum (large mass at high speeds). This propulsion method contrasts greatly with current technology ion drive propulsion which discharges much fewer exhaust particles (100 grams per day) at much slower speed (1% light speed (c)). Note following items:

1. With much less velocity and mass, ion drive exhaust particles have much less momentum than accelerated particles; thus, much less acceleration to vehicle.
2. Artificially assuming 100% efficiency and conservatively assuming exhaust particle velocity of .27c, g-force space travel requires fuel consumption of 1% ship's GW per day. A more practical assumption of much less then 100% efficiency would increase fuel requirements.
3. Thus, a g-force flight of 4 days duration could easily require many tens of thousand metric Tonnes; however, shipping just one Tonne of water from Earth's surface to space could prove problematic. What do we do??
4. There is a lot of water in space, for example Oort Cloud has trillions of comets; each has significant quantities of water and other ices (methane, ammonia, etc.). That might prove a good source of fuel for the future, but for the present we need something closer.
5. Stray comets occassionally come into Earth's vicinity. Thus, one solution would be to wait and harvest them until we're able to go where they reside in much greater numbers.
6. A more consistent source of water might prove to be the same source as for Earth. According to University of Iowa physicist, Louis Frank: "Thousands of comets daily bombard the Earth's atmosphere; they may account for Earth's oceans." If this proves true, our water problem could be easily solved.

For sake of further discussion, TE assumes water supply problem will be solved. Thus, TE assumes ample quantities of water for both fuel and inflight use (drinking, bathing, etc.) will be readily available.

Since 864 km/sec is way too fast to orbit Mars, spaceship must slow down. To continue g-force for the slow down portion of flight, we must decelerate at the same rate that we accelerated. Thus, distance/time for deceleration phase must equal distance/time for acceleration phase. At midpoint, we reverse direction of g-force propulsion vector as shown in diagram. Therefore, it takes another day of g-force deceleration to travel the remaining .25 AU to Mars. Total Trip Time Thought experiment assumes the commercial enterprise which planned, designed, built, maintains and operates the spaceship needs to make as many flights as possible to maximize Return On Investment (ROI). Thus, it assumes the spaceship's crew accomplishes a quick payload drop off at Mars with an immediate return to Earth. Thus, total trip time includes departure leg plus return leg. Let d be the distance from Earth to Mars, the departure leg. Since the time for the departure leg includes time to accelerate from Earth to midpoint(tAcc=√(d/g)) and time to decelerate from midpoint to Mars (tDec=√(d/g)) ; then total time for departure leg: t = tAcc + tDec = 2 √(d/g) For the example of traveling from Earth to Mars during opposition, departure leg equals acceleration phase plus deceleration phase for a total of .5 AU and two days of travel time. To return from Mars to Earth, we must accomplish departure leg in reverse. Assuming immediate return of spacecraft and slight movement between Earth and Mars during the very few days of this trip, thought experiment uses same value for distance/time for both departure and return legs. Total Time = Departure Time + Return Time tTtl = {tAcc + tDec} + {tAcc + tDec} tTtl = {√(d/g) + √(d/g)} + {√(d/g) + √(d/g)} tTtl = 4√(d/g) = 4√(.5 AU ÷ .5 AU/day2) = 4 days

Cultural History of Going to Mars

While current technology uses constant velocity spacecraft to reach Mars in several months, Edgar Rice Burroughs (ERB) conveniently reduced it to nothing. Famous for creating the Tarzan character, ERB also wrote a series of popular fictional novels about Mars.Several of Expanded Text.ERB’s Martian novels had as the main character, John Carter, an American, who goes to sleep in a mysterious cave in the Arizona desert and wakes up on the planet Mars (“Barsoom” to the natives). He meets with many incredible adventures as well as many exotic Martian creatures.Edgar Rice Burroughs was born on Sep 1, 1875, in Chicago, IL. His father had been a Union major in the Civil War. He attended good schools; but he did poorly academically. During his young adult years, he worked as a cowboy in Idaho, a gold miner in Oregon, a railroad policeman in Utah, a department manager for Sears, Roebuck in Chicago. He didn't start writing until the age of 35. ERB's first Mars book was written under the pseudonym Norman Bean. Most of his stories are written in the first person. Russian dictator Joseph Stalin once said that Edgar Rice Burroughs was his favorite author. An excellent guide to Burroughs' Mars books is "A Guide to Barsoom" by John Flint Roy.

Surprisingly, Edgar Rice Burroughs was inspired to write about Mars on the basis of then current science. Mars was always an intriguing world. From prehistorical times, Mars has been readily visible; however, the first recorded formal observation was by Aristotle in 356 B.C. Galileo viewed it through his telescope on Mars in 1610 to record the phases.In 1877, Schiaparelli was the first astronomer to identify the illusory features as Canals and produced a detailed map of Mars. This same year, the two Martian moons, Phobos and Deimos, were discovered. So there was a kind of ‘plausibility by association.’ If one new feature (the moons) were accepted, why not accept the other (the canals).Schiaparelli repeated and elaborated on his observations two years later in another close approach in 1879, eventually identifying some sixty distinct canal like structures. He called them ‘Canali’ or channels, which did not necessarily mean they were products of intelligent life. Canals were next observed nine years later by a pair of astronomers but only infrequently thereafter.Martian canals were being spotted independently by several observers, and their observations seemed fairly consistent. This suggested something real; so, the scientific and popular communities generally accepted their existence. Percival Lowell made his critical observations in 1892 and 1894 (close approaches of Mars to Earth) and wrote his popular book on Mars, undoubtedly read by Edgar Rice Burroughs. Next close approaches happened in 1907 and 1909; these would have put Mars prominently in the news once again, only a few years before Burroughs wrote A Princess of Mars.Percival Lowell published his book “Mars” in 1895, when Burroughs was twenty. The work’s popularity was evidenced by articles in the New York Times (35 articles from 1895 to 1910) and the serialization of “Mars” in the Atlantic Monthly (Summer of 1895). Thus, Burroughs was likely aware of Lowell’s ideas; and many of Lowell’s facts about Mars turn up in Burroughs’s Barsoom. These are some interesting parallels between Lowell’s Mars and Burroughs’ Barsoom; however, the most persuasive item is that it seems very likely that Burroughs used Lowell’s map in creating Barsoom. For more details, go to linked webpage: Burroughs’ Barsoom and Lowell’s Mars: A Map for the Interpretation of Barsoomian Geography by Leathem Mehaffey. Expanded Text.

Expanding the Range

Thus far, we've established a g-force range of .5 AU. Earth and Mars come this close about once every two years (Synodic Period = 758 days). We will increase this range.

TE assumes propulsion system will continuously increase capacity  such that ever increasing ranges will become more and more practical. Thought experiment assumes quick technology improvements such that exhaust particles will exit spacecraft at 86.6% c. Previous work indicates that 0.326% of ship's weight transformed into exhaust particles would suffice to maintain g-force for one day (artificially assume an unrealistic fuel efficiency of 100%). Following table assumes a much more realistic efficiency of 10%. G-force Fuel  Requirement for d = 1.0 AU Momentum Exchange (MX) Relativistic MX Practical Fuel Flow Mid-Way Fuel One-Way Fuel Two-Way Fuel ffMXDay = 0.326% GW/day ffRelDay = 0.163% GW/day ffPrac = 1.63% GW/day FMid = 2.03% GW F1-way = 4.06% GW F2-way = 8.12% GW 86,400sec/day × MShip dc×3.057×107 ffMXDay mr ffRelDay ε ffPrac × tAcc ffPrac  ×  t1-Way   = 2 × FMid  ffPrac × t2-Way  = 4 × FMid If VExh = .866c; then, dc=.866 Light speed/gravity = c/g= 3.057×107 mr=1/√(1 -  dc2) If dc = .866; mr=2.0  ε = Efficiency Factor Let ε =10%. tAcc  =  √(d/g ) = 1.414 days Let g=0.5AU/day² t1-way=2 √(d/g ) = 2.828 days t2-Way = 4√(d/g) = 5.656 days Thus, under above conditions, travel to/from a 1.0 AU destination would require about 6 days of g-force travel and about 8% of ship's Take Off Gross Weight (TOGW) for entire trip. Note that above table assumes that only 10% of fuel consumed actually transforms into effective exhaust particles (ε = .1); thus, ship must consume ten times as much fuel as needed for perfect propulsion engines with 100% efficiency.

Increase Performance Envelope.

Range of 1.0 AU (blue circle centered on Earth) intersects Mars orbit about 190 days before Earth-Mars opposition. Observing the Synodic revolution, Mars approaches Earth about 0.475°/day; thus, the 90° from about initial intercept of 1 AU circle to Earth-Mars opposition takes about 190 days.

Profile Range: 1.0 AU d dAcc tAcc VMax tDec t1-way t2-way F2-Way 1.0AU 0.5AU 1.41day 1,221 km/s 1.41dy 2.82 dy 5.64dy 8.12%TOGW Given d/2 √(d/g) g × tAcc √(d/g) 2×tAcc 2×t1-Way ffPrac×t2-Way g= .5AU day2 g= 864km/sec day tAcc  tAcc+tDec 4×tAcc ffPrac = ffMXDay ε×mr

During this 190 days from initial intercept of 1 AU circle (centered on Earth), the Earth-Mars separation decreases until the minimum at opposition.  After opposition, distance to Mars increases until the separation once again is 1 AU at another 190 days. Thus, Mars is within a 1.0 AU range for about 380 days every 25 months between Earth-Mars oppositions.  During this approximate 380 day period, g-force spacecraft would require less then one week's total propulsion time to travel to/from Mars. Dates for 190 days before (Nov 14, 2015)/after (Nov 28, 2016) opposition is easily determined using online Julian-Gregorian date converter.  Finally, NASA/JPL's excellent animated orbit tool can show how planetary positions change during these durations.

Range of 1.0 AU

increases g-force ship access to Mars.
For a 380 day duration (190 days before/after opposition)

out of each Earth-Mars Synodic Period (758 days),
a two way trip to Mars could take less than 6 days.
SLIDESHOW

---

---

---

---

VOLUME 0: ELEVATIONAL
VOLUME I: ASTEROIDAL
VOLUME II: INTERPLANETARY
VOLUME III: INTERSTELLAR

---

---

---

---