FULL MOON AND BEYOND: LAUNCH OMEGA
 L-4 and L-5 each forman equilateral triangle with Sol and Terra. |
|---|
| Habitats, Alpha and Omega, will be nice homes for a relatively few, but many more will visit. Alpha and Omega will directly benefit mankind and will prosper in return. |
| HABITATS CAN BE SAFE HAVENS. | |
 Alpha (α) and Omega (Ω) are arbitrary designations for the two Lagrange points in Earth's Solar orbit. For two body scenarios where one large body revolves around a much larger body (say Sol and Terra),Lagrange points have enhanced stability. Joseph-Louis Lagrange (1736-1813) discovered five positions where gravity forces equalize; the two most stable are L-4 and L-5. For the Sol-Terra system, L-4 (α) would lead Terra by 60° in Terra's orbit around Sol. L-5 (Ω) would lag Terra by 60°. Objects orbiting at these points are more likely to stay; thus, they make excellent "orbital parking spots". | Enhance Safety to Mother Earth and Humanity. α-Ω Habitats could be safe havens for asteroid resources harvested from interplanetary missions. It would be extremely good judgment to place such resources well away from Mother Earth. Other deep space habitats or even remotely piloted asteroid chunks could arrive from throughout the Solar System; their owner/operators might want to send them to Earth for final processing. However, huge chunks of extraterrestrial material entering orbits around Earth presents some impact risk. α-Ω Habitats could each host perhaps 100,000 to 1,000,000 people, sufficient population to process enormous quantity of extraneous asteroids and comets as well as to build other habitats and deploy them throughout the Solar System. At Habitats α-Ω, human colonies could process all such payloads at a safe distance from our home planet. At 1.0 AU from Earth, these habitats could safely harvest resources from far corners of the Solar System. |
| DISASTER EVENT VS. EXTINCTION EVENT. | |
| If an asteroid collides with a space borne habitat, worst case would be a disaster with significant loss of life. If a asteroid collides with Earth, scientific studies of previous such events indicate this would likely be an extinction event with total loss of life on planet Earth. Obviously, one would choose the disaster over the extinction. Furthermore, if such an extinction occurs (in spite of precautions), human survival might depend on alternate human populations on large terraformed habitats with plentiful amounts of Terran topsoil, flora and fauna. Asteroid collisions occur naturally, but human error can play a part when we start harvesting asteroids. As we maneuver asteroids back to orbit Earth for much easier processing; it's possible that human error could someday cause an orbiting asteroid to impact Earth. We don't want such events on our home planet; thus, it makes a lot of sense to send these asteroids to nearby habitats to conduct the processing. SPACE-BORNE ECONOMICS. As interplanetary vessels prowl the Solar System and collect materials, they will bring them not to Terra Firma (Earth) where they might prove hazardous to the Mother Planet, but to Habitat α-Ω to be easily processed. A likely economic model could have the habitats paying a delivery fee to relevant interplanetary vessels; thus, detecting and collecting plantesimals will prove to be lucrative. Furthermore, Habitats α-Ω will process these materials to add considerable value and then sell them to other vessels traveling to other destinations. Thus, living on Alpha/Omega will also prove lucrative. |  Habitats need agriculture. Thus, they'll likely need to stop by Habitat α-Ω to buy some supplies, such as: 1) Energy Sources. Habitats in Earth Orbit will likely use large external mirrors to reflect sunlight into habitat. 2) Water Sources. Initially from Terran oceans; eventually from space borne comets. Obviously needed to grow crops as well as other life support purposes: drinking, bathing, swimming, even fishing. 3) Seed Sources. Import large quantities of Terran topsoil to initiate habitat terraforming. Hydroponics might provide some food, but habitat still needs lots of topsoil to plant trees for oxygen, fruit, wood; even for landscaping. |
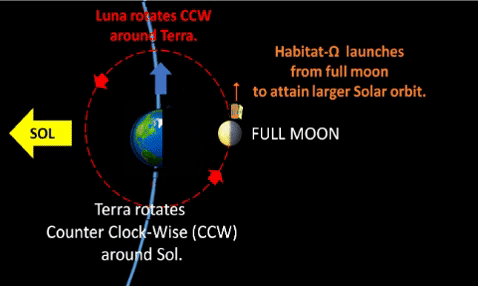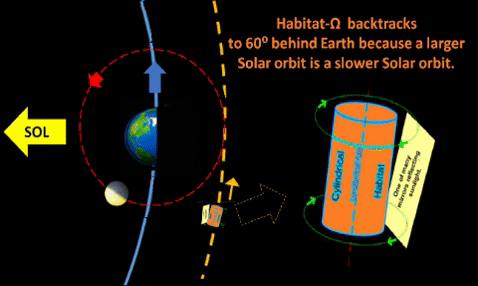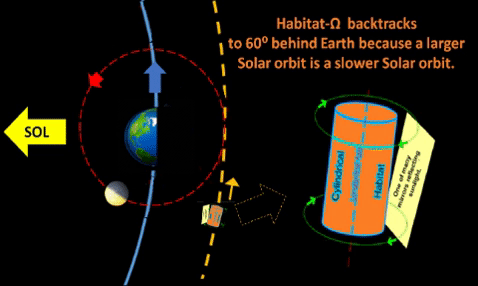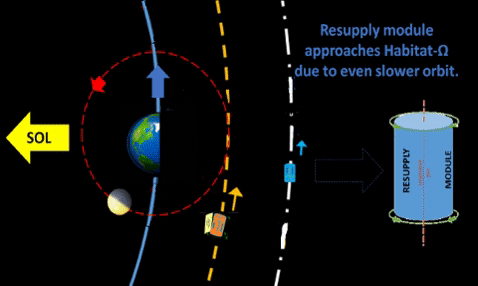
FULL MOON
During Luna's orbit about Terra, it will enter the Full Moon phase
when it is on opposite side of Sol, and we observe a fully illuminated Moon. FinSome see a Lunar Eclipse when the Earth's shadow covers the Full Moon. | |
 |
Habitat Omega (Hab-Ω) could launch from aft end of Full Moon for insertion into a Solar orbit with slightly larger orbital radius and slightly slower angular velocity. Thus, a Full Moon launch enables a vehicle to lag Mother Earth in Earth's own orbit.
If Hab-Ω separates from the Luna-Terra system and continues a tiny daily lag rate of .004°/day; then, it would take 15,000 days (about 41 years) to reach 60° behind Earth's orbital position. Thereafter, Hab-Ω can rejoin the Terran Solar orbit and "park" at the L5 point to maintain a 60° lag from Earth.
This 40+ years transit time can be put to good use with lots of construction with materials from following launches from Luna.
|
 |
Getting There
Consider likely progress of Hab-Ω
during initial Lunar cycle Omega Launch Tables After Lunar Launch, note continual increase of linear separation (distance, d) of Hab-Ω from Terra. |
|---|---|
| SOLAR ORBIT | |
|---|---|
Assume first Full Moon happens exactly when Terra crosses line from Sol to “Point of Aries (♈) as shown to the far right of Sol in the diagram. Further assume mean Lunar radius (RL) of 384,000 km. If Hab-Ω carefully launches from Luna at Full Moon phase, it achieves a Solar Orbit of 1 AU + RL .
1 AU + RL = 149,597,870.7 km + 384,000 km
Inset rectangle shows Hab-Ω progress during first Lunar Cycle (Full Moon to Full Moon), a duration of 29.5 days.1 AU + RL = 1 AU + .00257 AU = 1.00257 AU
For convenience,
let angular velocity (ω) = mean motion (n) for both Terra and Hab-Ω. Assume HabΩ Mean Motion nΩ = 0.9829o/dy Assume Earth Mean Motion n♁ = 0.9867o/dy Finally, assume that during the approx. 40 year transit time from Lunar launch to L5 (i.e. a lag of 60°), Hab-Ω closely parallels Terran orbit, a near circular orbit with slight eccentricity, e. |
 |
| FIRST LUNAR CYCLE | |
|---|---|
 |
During Full Moon (assume Aries), Hab-Ω launches from “aft” side of Luna.
Assume enough propulsion to barely escape gravity of Terra-Luna system and maintain Solar orbit of 1.00257 AU. Slightly greater Solar radius will cause slower angular velocity and Hab-Ω will gradually lag further and further from Terra. CONSIDER: Will Hab-Ω avoid Lunar collision during this critical first Lunar Cycle? Omega Launch Table indicates that such collision is unlikely. Immediate Lunar motion is distinctly away from Hab-Ω in its Solar Orbit; thus, collision is unlikely as long as Hab-Ω escapes Luna’s gravity. Remaining question, will Luna collide with Hab-Ω when it returns to Full Moon position. Again, this is very unlikely. EXAMPLES: 1) Midway thru 1st lunar cycle (New Moon phase), Hab-Ω has already traveled over 434,000 km from Terra which exceeds max Lunar radius from Terra, 407,000 km. 2) At end of the cycle, Luna is back at Full Moon position and thus near Hab-Ω ‘s Solar radius. At this time, Hab-Ω’s separation from Terra is over 542,000 km, well out of Luna’s reach. Finally, Hab-Ω must orbit for about 40 years in transition orbit (1.002547 AU from Sol) until it is 60⁰ behind Terra. Then, space tug pushes it into Earth orbit (1.0 AU from Sol) to indefinitely maintain that 60⁰ lag. |
Assume Hab-Ω needs
resupply modules (Hab-Mod).
Deployment method might use
deeper orbits beyond FULL MOON.
TE assumes it to be very impractical to launch entire Hab-Ω with supplies for all 40 years, with all payloads, with all personnel at the very first launch. Thus, TE suggests additional resupply modules during next few Lunar Cycles. .See following diagrams for more details. |
 |
| SECOND LUNAR CYCLE Subsequent Full Moons present more opportunities for resupply missions. | |
|---|---|
To survive the long voyage of orbiting from Earth to a parking spot 60° (one AU) away, launch additional Habitat-Modules (Hab-Mods) with more supplies and materials. During second Lunar Cycle, we can demonstrate one such launch.
❶ At start of 2nd Lunar Cycle (Full Moon), Habitat Module (Hab- Mod) leaves Lunar Orbit for a larger slower orbit to gain a lag rate greater than Habitat-Omega (Hab-Ω) .
❷
Halfway through 2nd Lunar Cycle (New Moon), Hab-Mod
falls behind Terra.
❸
At next Full Moon, Hab-Mod catches up with Hab-Ω and must quickly rendezvous for a
permanent rejoin.
|  |
 |
At start of 2nd Lunar Cycle, Thought Experiment (TE) assumes that Terra and Full Moon line up at 29.108⁰ from previously discussed “Line of Aries” when Hab-Ω first launched.
Finally, TE assumes: A. 1st burn to leave Lunar Orbit, B. 2nd burn to join new orbit, C. Hab-Mod parks as shown in selected orbit. |
Midway through 2nd Lunar Cycle, Luna enters the New Moon Phase as shown. TE assumes Hab-Mod achieves 43.3⁰ as shown.
|  |
 |
At completion of 2nd Lunar Cycle, TE assumes that Hab-Mod catches up with Hab-Ω; thus, both line up at 57.008 ⁰.
Not shown are the burns which Hab-Mod must do to leave its orbit and join up with Hab-Ω.
CONCLUSION: Wait one month to launch 1st resupply module, which takes another month to catch up with Hab-Ω; thus, 2 month interim.
HYPOTHESIS: Wait 2 months to launch 2nd resupply module, which takes another 2 months to catch up with Hab-Ω; thus, 4 month interim and so on for subsequent modules.
|
| THIRD LUNAR CYCLE | |
 |
At the end of 3rd Lunar Cycle since launch of Hab-Ω, all 3 resupply modules reach slightly different radii from Sol. As radii increase, their Solar angular velocity decreases as shown. |
 |
FOURTH LUNAR CYCLE
EXAMPLE: At start of 4th cycle (since initial launch of Hab-Ω), all 3 resupply modules launch from Luna to achieve 3 different Solar orbits as shown in previous diagram.
During 4th Lunar cycle, they drift away from Terra and toward Hab-Ω, which continues a slowly increasing lag behind Earth.
At end of 4th Lunar Cycle, Mod-3 will align with Hab-Ω and will use several “burns” to descend to Hab-Ω’s orbit and link up. |
FIFTH LUNAR CYCLE
During 5th Lunar Cycle, remaining two resupply modules drift closer toward the Solar angle of Hab-Ω, still slowly increasing lag from Earth; Mod-2 even approaches the Solar angle of Hab-Ω. By end of 5th Lunar Cycle, Mod-2 makes its way from a greater Solar radius to link up with Hab-Ω. |
 |
 |
SIXTH LUNAR CYCLE
During sixth Lunar Cycle since launch of Hab-Ω, remaining resupply module drifts very close to and almost aligns with the Solar angle of Hab-Ω.By end of 6th Lunar Cycle, Mod-3 makes its way to link up with Hab-Ω. |
This slightly larger orbit enables Hab-Ω to consistently lag the Earth at a very small rate, slowly increasing its angular distance behind Terra. Though this lag rate stays tiny, it will eventually accumulate into the 60° lag to park at the L-5 point; at this rate (about .004°/day) it might take 40+ years to eventually reach its final parking sport, 60° behind Terra.
CONCLUSION: 40+ years is a long time to wait for a parking spot; perhaps, there is a quicker way.
TRANSITION: Perhaps, Hab-Ω can leverage Earth's elliptical orbit to arrive much sooner than 40+ years. See next chapter, Earth's Ellipticity.
posted by JimODell at 2:14 AM
0 Comments:
Post a Comment
<< Home