MASS TO MOTION

CONTENTMOMENTUM EXCHANGETABLE-1. Short Range: 0.2 to 1.0 AUMIXED UNITSTABLE-2. Midrange: 1 to 5 AURelativistic UnitsTABLE-3. Long Range: 5 to 25 AUTABLE-4. Longer Range: 10 to 50 AUSidebar: Robert Goddard

Converting mass to motion
is a simple fact of life.

---

Our bodies do it
when we walk around the block.

---

  We do it with planes,
trains and automobiles.

---

  Our thought experiment's spaceship does it
to accelerate to nearby planets.

---

---

---

---

---

Robert Hutchings Goddard (October 5, 1882-August 10, 1945). Throughout his extremely productive life, Goddard realized the potential of missiles for space flight and greatly contributed to practical realization. As a teenager, Robert Goddard, read a serialized version of H. G. Wells's War of the Worlds and began filling notebooks with ideas for interplanetary travel. In 1907, Goddard first gained public notice from a powder rocket which produced a huge cloud of smoke in the physics building of Worcester Polytechnic Institute.	Most people routinely buy fuel for their automobiles. We all know the purpose of gasoline is to enable vehicles to travel; thus, mass converts to motion as fuel ignition powers the engine to move the car down the road. Stop refueling, and the gas gauge eventually drops to zero, and motion stops; thus, we intuitively know that fuel consumption is another fact of life. %TOGW = Fuel/MShip Of course, aircraft flight also depends on fuel; some aircraft designers use the term, Percent Take Off Gross Weight (%TOGW), to indicate portion of aircraft's initial gross weight needed for fuel at beginning of flight. EXAMPLE: At beginning of trip, let a ship's total weight be 100 tons with 60 tons of fuel, then  %TOGW = 60 tons/100 tons = 60% for that particular trip. With a %TOGW of 60%, ship must limit all other mass (infrastructure, payload) to 40% of ship's mass. Since payload is the purpose of any trip, we want to minimize %TOGW.
Basic Assumptions: In free space (no air resistance), an object will travel at a constant velocity until a force acts upon it. Let our thought experiment's spaceship eject particles for an entire second; the particle momentum (collective mass times their velocity) will force the spaceship to react accordingly by changing it's velocity. MShip × VShip = mfuel× vExh Thought experiment assumes that collective exhaust particle momentum throughout a second can be described by one vector (direction and length); thus, thought experiment further assumes an equal and opposite vector describes spaceship's momentum for same duration (one second). MShip × VShip 1 sec = mfuel × vExh 1 sec Thought experiment's main premise: spaceship travels at g-force throughout entire voyage; thus, the vessel's velocity must increase by 10 m/sec for every second. Of course, this value approximates acceleration rate of free falling objects near Earth's surface. According to Einstein's famous thought experiment, occupants will feel same weight sensation as if they were static on Earth's surface. Thus, we're constrained to use the value 10 m/sec for the term, VShip.  Since we specify that value for every second of flight, we can substitute g (=10 m/sec2) for VShip/sec. MShip × g = mfuel × vExh 1 sec	In 1914, Goddard received his first two U.S. patents. Liquid fueled rocket. Multi-stage rocket using solid fuel. Altogether, Robert Goddard developed 214 patents; many were awarded posthumously. In Goddard's" autobiographical essay: "on the afternoon of October 19, 1899, I climbed a tall cherry tree and ….. looked towards the fields at the east, I imagined how wonderful it would be to make some device which had even the possibility of ascending to Mars ...." He died on August 10, 1945, four days after the first atomic bomb was dropped on Japan. Expanded Text
Progressive Elaboration Following series of tables will be modified in constructive ways. Independent Variable (IV). Thought experiment (TE) presumes humanity will eventually use on board particle accelerators to expel continuous streams of high speed exhaust particles.  These collective particles will be of sufficient quantity to propel the space vessel at continuous g-force.  TE further presumes continual improvement of these on board particle accelerators such that the particle exhaust velocity (VExh) will continually increase. Thus, first table independently varies VExh over a specified range. Subsequent tables will show VExh in higher ranges. Dependent Variable (DV). Previous work shows that MShip depends on VExh. Thus, TE further presumes that as VExh increases, that initial results will see a corresponding increase in ship size, MShip.  MShip = mfuel 1 sec × vExh g Fuel. For each second of space flight, a collective mass of fuel is consumed; then, it transforms into ions and accelerates into near light speed exhaust particles.  Thus, this Thought Experiment chooses a quantity which best draws useful conclusions.  Thus, we initially choose a value of one kilogram of mass (mfuel) for every second of powered flight. Furthermore,let us express this mass per second (mfuel/sec) as fuel flow per second (ffsec). MShip = ffSec × vExh g TE assumes for every second of flight, one kilogram of fuel can be superheated and ionized into plasma particles which can be collected and accelerated by well placed electromagnetic fields to very high exhaust speeds.  Since there are 86,400 seconds per day; fuel flow per day can be described: ffDay = 86,400× ffsec = 86,400 kg/day == 86.4 mT/day With trip time, t, in days, determine total fuel, F, for trip: F = ffDay × t Finally, this lets us compute percent Take Off Gross Weight, %TOGW, portion of ship's initial gross weight needed for fuel.  %TOGW = F/MShip RECALL, an increase in VExh. will increase ship size, Mship. Thus, an increase in VExh will decrease the %TOGW value.	MOMENTUM EXCHANGE Rocket Exhaust = Ship Propulsion mfuel × vExh = Mship × Vship mfuel : Mass of fuel consumed. vExh : Velocity of fuel particles exiting exhaust. Mship : Mass of Spaceship. Vship : Velocity of Spaceship. CONVERT TO RATES On each side of equation, divide selected term by one second. mfuel 1 sec × vExh = Mship × Vship 1 sec Select VShip = 10 meters per sec. VShip 1 sec = g = 10 m/sec 1 sec Fuel flow per second ffsec = mfuel 1 sec MShip × g  =  ffSec × vExh EXAMPLE: Let particle exhaust speed, vExh = 30 million m/sec. Mship = ffsec × vExh g Mship = 1 kg/sec × 30,000,000 m/sec 10 m/sec2
From Earth, there are many useful targets within 1 AU. Many scientists would love a g-force spaceship to travel in this area within a few days vs months at orbital velocity.	TABLE-1. Constant g-force Acceleration Short Range: 0.2 to 1.0 AU. INITIAL FUEL PROFILE: No slowdown. Assume fuel flow per second: ffsec = 1 kg Thus, also assume daily fuel flow: ffDay = 86,400 kg . Given dist.(d) 0.2 AU 0.4 AU 0.6 AU 0.8 AU 1.0 AU t=√(2d/g) time (t) 0.89 dy 1.26 dy 1.55 dy 1.79 dy 2.0 dy  864 kps / day = g  = 10 m/sec² =  g =  .5 AU /day   VFin=t×g Vel.(VFin) 769kps 1,089kps 1,339kps 1,547kps 1,728kps F=ffDay×t fuel (F) 77,279kg 109,228kg 133,850kg 154,557kg 172,800kg vExh mega-m/s MShip megakg %Take Off Gross Weight (%TOGW) 10 1 7.73% 10.93% 13.39% 15.46% 17.28% 20 2 3.86% 5.46% 6.69% 7.73% 8.64% 30 3 2.58% 3.64% 4.46% 5.15% 5.76% 1kg/s×vExh 10m/sec2 = MShip %TOGW = F MShip
Recall Effects of Constant Acceleration Let d equal straight line distance from departure to destination. g ≈ 10 m sec2 g ≈ (86,400 sec)2 sec2 × day2 × 10m × AU 1.5x1011 m g ≈ 0.5 AU day2 From Newton's laws of motion: d = 1/2 × g × t2 Solve for t:  t = √(2 d / g ) Let g be same acceleration as experienced in free fall near Earth's surface. For convenience, assume g closely approximates 10 m/sec2 Straightforward conversions allow us to further assume g approximates 0.5 AU/day2.   EXAMPLE: Let d=0.4 AU, then calculate trip time for constant acceleration for entire distance: t  = √(2 × 0.4 AU / 0.5 AU/day2) = 1.26 days One can compute travel distance with trip time as independent variable. Thus, solve for d: d =(1/2) × g × t2  EXAMPLE: Accelerate at 0.5 AU/day2 for .9 days; then, determine distance traveled: d = 0.5 × 0.5 AU/day2 × (.9 day)2 = 0.202 AU	WARNING!!!!!!!!!!!!! After only one day of g-force acceleration, spacecraft attains enormous velocity: vFin = 864 kilometers per second! Assume velocity increases 10 m/sec for every second of g-force propulsion. vFin = tsec × g = 86,400 sec ×10 m/sec² vFin = 864,000 m/sec = 864 km/sec STATE ANOTHER WAY. For every day of constant acceleration, g; spacecraft velocity increases 864 km/sec: EXAMPLE: After two days of g-force spaceflight: vFin = g × t = 864 km/sec /day × 2 days = 1,728 km/sec To accommodate these enormous speeds  interplanetary g-force space travel needs FLIGHT PROFILE: Slowdown at midpoint.

Operational range to 5.0 AUs expands options of notional spaceship: 1) anywhere on Martian orbit, 2) large portion of asteroid belt, 3) selected portion of Jovian orbit.

Mix Units. To conveniently avoid large cumbersome numbers. Mix velocity units: Express exhaust particle speed, VExh. as decimal light speed, dc. % c dc*c meters/sec 10% .1 c 30,000,000 20% .2 c 60,000,000 30% .3 c 90,000,000 Express velocity incremental increase per second as g, VShip/sec = g = 10 m/s2 g = 86,400 sec/day ×10 m/sec2 = 864 kps/day g = 86,400 sec/day×864 kps/day = 0.5 AU/day2 Mix mass units: Use metric Tonnes (mT) for ship size, MShip 1 mT 1,000 kilograms 1,000 mT 1,000,000 kg Use kilograms for fuel flow per second, ffsec. Mship = ffsec × dc × c g Let ffsec = 1 kg/sec then replace constant c/g with: K = 30,000 Mship= ffsec × dc × 30,000 Let ffsec = 1 kg/sec vExh(dc × c) Mship .1 c 3,000 mT .2 c 6,000 mT metric Tonnes in fuel flow per day, ffDay. While we now set fuel flow to only 1 kg/sec, this will quickly add up to many thousands of kgs. ffsec = 1 kg/sec ffDay = 86,400 kg/Day ffDay = 86.4 mT/day F = t × ffDay Thus, express total fuel, F, in mT, metric Tonnes.

Adjust Flight Profile A better flight profile would accelerate to halfway then slowdown. Thus, expression for total time of travel changes to  t = 2√(d/g) which is explained further below. To accommodate enormous velocity gains and still maintain g-force throughout the entire flight, accelerate at g-force until the halfway point; then, decelerate at g-force for remaining half of time/distance. Consider it axiomatic that the two halves of the flight duration are equal. The main difference between these two flight phases is that the ship's propulsion vector will point in opposite directions. TABLE-2. Accelerate to Halfway Midrange: 1 to 5 AU Adjust Flight Profile to accommodate slowdown from midpoint of trip. Given dist. (d) 1 AU 2 AU 3 AU 4 AU 5 AU t = 2√(d/g) time (t) 2.8dy 4.0 dy 4.9 dy 5.66 dy 6.32 dy F = ffDay × t fuel (f) 244mT 346mT 423mT 489mT 546mT vExh = dc c MShip %Take Off Gross Weight (%TOGW) .1 c 3,000 mT 8.15% 11.52% 14.11% 16.29% 18.21% .2 c 6,000 mT 4.07% 5.76% 7.05% 8.15% 9.11% .3 c 9,000 mT 2.72% 3.84% 4.70% 5.43% 6.07% .4 c 12,000 mT 2.03% 2.88% 3.53% 4.08% 4.55% g≈0.5 AU/day2 ffDay=86.4mT/dy c≈3×108 m/sec 30,000×dc %TOGW = F MShip If g-force vessels accelerates for entire distance from departure to destination, determine travel time as shown in TABLE-1:  t = √(2 ×  d / g ) However, if the acceleration distance (dAcc) is half of total distance (d/2); then, determine acceleration time as shown.  tAcc = √(2 ×  dAcc / g ) Substitute d/2 for dAcc.   tAcc = √(2 × d/2 / g ) tAcc= √(d/g) To gracefully intercept destination, ship must decelerate during 2nd half of trip. To maintain Earth like gravity, ship must decelerate at g-force. Thus, apply equal but opposite propulsion vector for same distance/time as for acceleration leg. Thus, let deceleration time equal acceleration time.  tAccel = tDecel Thus, we can double the above acceleration time to halfway and determine entire 1-way travel time. tTtl = tAccel + tDecel= 2√(d/g) = t EXAMPLE. For trip distance = 5 AU, we can determine trip as follows: 2√(5 AU / 0.5 AU/day2) = 6.32 days

Relativistic Units THOUGHT EXPERIMENT'S MAIN ASSUMPTION

Exhaust particles gain enormous velocity, V_Exh, prior to exiting spacecraft.

V_Exh is a significant portion of c, speed of light.

Thus, V_Exh adds enormous momentum to propulsion particles as they exit the spacecraft.

---

Thought experiment further assumes that relativistic mass growth imparts even more momentum which adds even more mass capacity to the spaceship. This growth can be quantified by the Lorentz Transform.

LORENTZ TRANSFORM

①	Compare exhaust particle's original mass (mO) with increased relativistic mass (mr). mr = mO √(1-v2Exh/c2)	②	Let mO = 1; then, mr = 1 √(1-v2Exh/c2)
③	Substitute dc × c for vExh; then, ② reduces to: mr = 1 √(1 - dc2)	④	Let mO = ffsec Let original mass be the fuel consumed at rest.  To indicate this quantity, TE uses "ffsec", fuel flow per second.  To indicate mass of exhaust particles per second, TE uses "ffExh".
⑤	Show relativistic growth of fuel particles; consumed fuel,  ffsec, becomes high momentum exhaust particles, ffExh. ffExh = ffsec √(1 - dc2)	⑥	Expressed another way: ffExh = mr × ffsec Example: Let VExh= dc  × c = .3 c mr =1.0/√(1 - dc 2) = 1.0/√(1-.32) ffExh = mr × ffsec   = 1.048 ffSec
⑦	To account for relativistic effects on exhaust particles, momentum exchange equation should use  ffExh. Mship = ffExh × vExh g	⑧	Make suitable substitutions: vExh = dc × c ffExh = mr × ffsec Mship = mr ffsec×dcc g
⑨	c ≈ 300,000,000 meters/sec g ≈ 10 meters/sec/sec Express ffsec in kg; Mship in mTs; Conversion: 1kg = 10-3 mT Replace c/g with 30,000 Mship = mr×ffsec×dc×30,000	⑩	dc ffExh Mship .1 1.005 kg 3,015 mT .2 1.021 kg 6,124 mT .3 1.048 kg 9,435 mT vExh/c 1 kg/√(1-dc²) ffExh × dc × 30,000

TABLE-3. 2-Way Fuel Plan

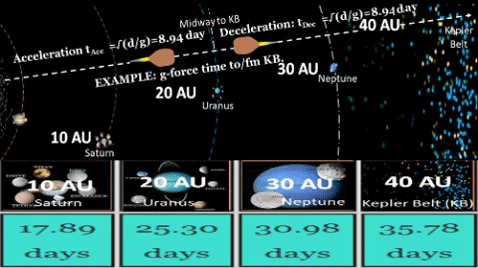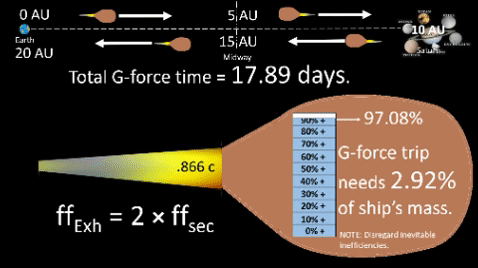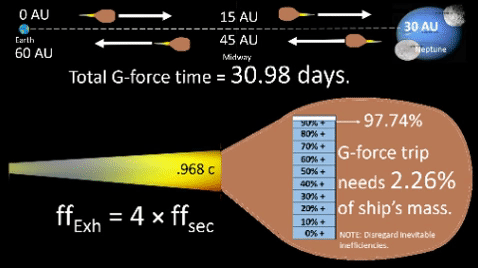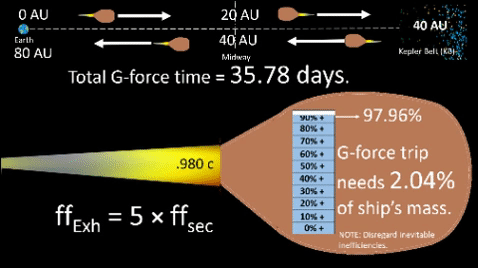
distance	Given	(d)	5 AU	10 AU	15 AU	20 AU	20 AU range includes orbits of Jupiter and Saturn as well as large portion of orbit of Uranus.
time	4√(d/g)	(t)	12.65days	17.89days	21.91days	25.30days	To accommodate two way trip, double the time factor from 2√(d/g) to 4√(d/g).
Fuel	ffDay×t	(F)	1,093 mT	1,546 mT	1,893 mT	2,186 mT	ffDay = 86.4 mT /day
vExh(dc×c)	ffExh	MShip	%Take Off Gross Weight (%TOGW)				2-Way Flight Profile: assumes four phases of equal duration as described below. Phase 1: Accel from dept to midway, t= √(d/g). Phase 2: Decel from midway to dest, t= √(d/g). Phase 3: Accel from dest to midway, t= √(d/g). Phase 4: Decel from midway to dept, t= √(d/g).
.3c	1.048kg	9,435 mT	11.59%	16.39%	20.06%	23.17%
.4c	1.091kg	13,093 mT	8.35%	11.81%	14.46%	16.70%
.5c	1.155kg	17,321 mT	6.31%	8.93%	10.93%	12.62%
.6c	1.250kg	22,928 mT	4.77%	6.74%	8.26%	9.53%
.7c	1.400kg	29,965 mT	3.65%	5.16%	6.32%	7.30%
.8c	1.667kg	40,760 mT	2.68%	3.79%	4.64%	5.36%
Given	ffSec √(1-dc2)	ffExh×dc×30,000	%TOGW = F / MShip

Derive Mass to Motion How Much Mass Does Motion Take??? From direct inspection of prior tables, we conclude that VExh directly affects %TOGWDay which in turn determines overall %TOGW. A %TOGWDay = ffDay MShip Axiomatic: Define %TOGWDay One day's fuel flow (ffDay) divided by initial mass of the ship will give us the proportion of ship's mass needed for that daily fuel. B ffDay = 86,400 secs Day × ffSec Axiomatic: Define ffDay Multiply one second's fuel flow (ffsec) times 86,400 seconds/day to closely approximate one day's fuel flow. C MShip = mFuel/Sec × vExh VShip/sec MShip = ffExh× vExh g MShip = mrffsec× dcc g Recall following identities from previous work. --Let VShip =10 m/sec; then, VShip/sec = g, acceleration as if due to Earth's gravity. --mFuel/sec = ffExh = mr×ffsec, where mr is the factor from Lorentz Transform. --vExh = dcc, decimal coefficient times light speed. D %TOGWDay = g × 86,400 ffSec mrffsec × dcc Rewrite %TOGWDay Percent of TakeOff Gross Weight (%TOGW) for first day can be rewritten as shown with substitutions for ffDay and MShip. E mr = 1 √(1-dc2) Recall mr identity from Lorentz Transform. Rewrite to identify dc, light speed coefficient. dc = √(mr2-1) mr F %TOGWDay = g×86,400 c × 1 mr × dc %TOGWDay = g×86,400 c × mr mr×√(mr2-1) Rearrange D; then, substitute dc identity from E. G %TOGWDay = 0.283%/day √(mr2-1) Given precise values: g = 9.80665 m/s2; c = 299,792,458; day = 86,400 sec; day × g ÷ c=.002826 ≈ 0.283% and F becomes G.

TABLE-4. Longer Range: 10 to 40 AU DAILY FUEL CONSUMPTION. Adjust Fuel Profile to directly determine daily decrease in ship's mass due to expulsion of propulsion particles. Thus, we no longer need to compute daily fuel requirement (ffDay) and compare to ship size (MShip). We can directly determine percentage mass decrease of ship's mass. Thus, delete fuel mass row from TABLE-3, and %TOGWDay column replaces TABLE-3's ship size (MShip) column. Tables focus on %TOGW, a relevant parameter of space flight. They show that TOGW varies according to speed of exhaust particles. TOGW does not depend on distance, time or fuel which our table keeps static. (Subsequent blogs consider effects of varying fuel consumption; eventually, consider effects of varying g.) As vExh grows, ship size (MShip) grows dramatically; thus, ship size depends on particle momentum but total fuel consumption still depends on distance/time. Thus, for the same distance, %TOGW (= Fuel / MShip) decreases dramatically as vExh grows. For increasing distances, %TOGW as distance increases and decreases monotonically as vExh increases. Thus, we conclude... %TOGW is the amount of ship's mass that must convert to kinetic energy (i.e., "motion") as g-force accelerates it throughout the entire trip. Furthermore, the converted energy does other things. TE spaceship must use the accelerated particles for propulsion, but some energy will be needed for ship's life support, navigation, communication, entertainment. Even the propulsion system draws energy which doesn't directly propel the vessel; the particle acceleration process requires energy for the many components (magnets, particle detectors, etc.) of the accelerator which need lots of energy. %TOGWDay = ffDay MShip = 86,400 × ffsec 30.57 √(mr2-1) × 106 × ffsec = 0.283%/day √(mr2-1) %TOGWTtl = t × %TOGWDay = t × 0.283%/day √(mr2-1)

%TOGW depends on mr, relativistic growth factor and time, t. As shown in above equation, %TOGW is inversely proportional to mr. As it grows, %TOGW shrinks which means less matter needs to convert to energy for same days performance. Thus, more of ship's GW can be devoted to payload, a good thing. Father of Modern Rocket Propulsion Sidebar: Robert Goddard

Electric Propulsion RHG's Early Career.  As a young academic, he divided his time between official research on electricity and his personal passion for propulsion. This led him to Electric Propulsion (EP).  In modern times, we wonder why was Goddard more concerned with the electrostatic acceleration of electrons rather than ions? (Recall that ions are much more massive than electrons; thus, they contribute far more momentum between the rocket and exhaust particles.) An online paper suggests five reasons: The nature of cathode rays was still debated at that time, and the ionization of electron-ion pairs was not understood as fully as now. In those years, most experts considered high accelerating voltages (vs. high beam currents) as the main technical difficulty. Thus, electrons seemed better suited for very high velocities. Most did not yet appreciate how special relativity impacted the acceleration of a particle from rest to near light speed (c). Most likely, Goddard did not fully appreciate the practical (i.e., system-related) penalty incurred by an electric rocket with an exceedingly high exhaust velocity. Electrostatic acceleration requires large accelerators. As in many other instances in his highly prolific career, his brilliant EP ideas went largely unrecognized. TWO PRIME EXAMPLES:  1) In 1913, he submitted patent for an ionization chamber.  This device used a magnetic field to confine free electrons to produce ions from neutral molecules in a surrounding gas. 2) In 1917, Goddard, submitted first patent for electrostatic ion accelerator to aid propulsion, i.e., an ion thruster.

SLIDESHOW

---

---

---

---

VOLUME 0: ELEVATIONAL
VOLUME I: ASTEROIDAL
VOLUME II: INTERPLANETARY
VOLUME III: INTERSTELLAR

---

---

---

---