A Thought Experiment: HABITATS CAN CYCLE TO MARS

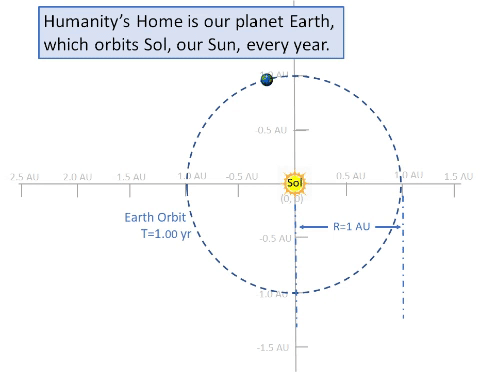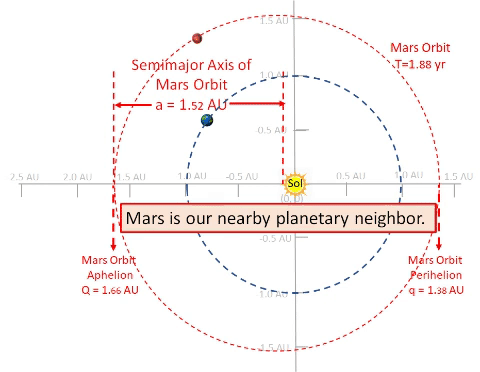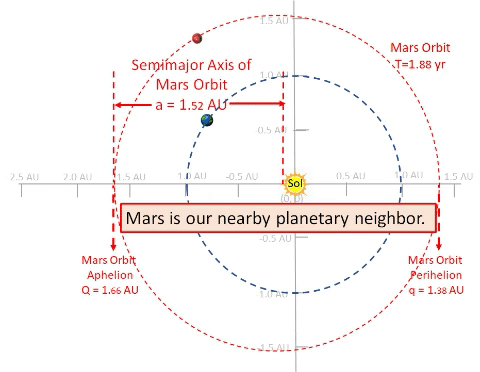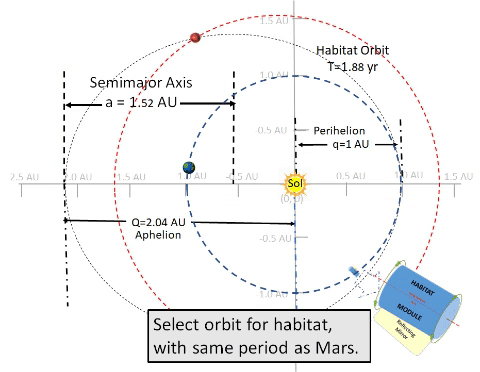Consider a notional habitat orbit which intercepts orbits of Earth and Mars. Let this orbit have same period as Mars (1.88 years). With a well designed orbit, a habitat could rendezvous with Mars every period. (See Marsonance TABLE.)

This orbit might have a perihelion (q, closest point to Sol) of 1.0 AU, radius of Earth's solar orbit. With this orbit, habitat might also rendezvous near Earth once per many periods.

Unfortunately, Earth rendezvous opportunities would be rare because the orbital period (1.88 years) is same as Mars's orbit (1.88) but not Earth's period (1 year); this, Habitat resonates with Mars but not with Earth.

CONSIDER ORBITS TO RESONATE WITH MARS.

**a = 1.52 AU**
Focus (c): **c = a - q**;
thus, c² = a² -2aq + q²
Furthermore, b² = a² - c²;
thus, b² = 2aq - q² = q (2a - q)
**Semi-minor Axis (b):**
0<q<a	b= √(q(2a-q))	ℓ = b² / a
Perihelion q	Semiminor Axis b	SemiLatis Rectum ℓ
(AU)	(AU)	(AU)
0.2	0.75	0.37
0.4	1.03	0.69
0.6	1.21	0.96
0.8	1.34	1.18
1	1.43	1.34
1.2	1.49	1.45
1.4	1.52	1.51

Thought Experiment (TE) assumes an existing asteroid could transform into a habitat,
and orbit could be modified for continuous habitat transfer between planets.
For continuous cycling between asteroidal Habitat and planet Mars,
choose Habitat Period (T_H) to equal period of Mars (T_♂),

T_H= 1.88 yr = 686.67 days = T_♂
Per Kepler's Third Law, use T to determine semimajor axis (a):
a = ∛(T²) = ∛(1.88²) = 1.52 AU
For any orbit, perihelion (q) can be any nonzero value
up to a maximum of "a", semimajor axis.
Thus, express "q" as %a.

q	%a = q (AU)	q = 39% a = .6 AU	q = 66% a= 1.0 AU	q = 92% a= 1.4 AU
e	(a-q) / a	e = .605	e = 0.342	e = .079
Eccentricity (e) quantifies "flatness" of orbit.
Remarks:		For q < 1.0 AU , Habitat orbit intercepts Earth orbit at two points;this increases frequency of actual rendezvous event with Habitat and Earth.	For q = 1.0 AU, Habitat orbit might intercept Earth orbit at q,but it's very unlikely that Habitat will actually rendezvous with Earth at time of intercept.	For q > 1.0 AU, Habitat orbit does not intercept Earth orbit; thus, a habitat cannot use this orbit to transfer from Earth orbit to Mars orbit.

MARS CYCLER WILL RARELY RENDEZVOUS WITH EARTH.

For simplicity, assume all three orbits to be coplanar; inclination is considered later.

Most Solar objects orbit in a counter clockwise (CCW) direction as observed from north of the Earth.

Most solar objects use a reference ray at orbit's perihelion, q. Thus, Habitat's angular distance (Θ) is 0° at q, and increases in a CCW direction.

Arbitrarily design Habitat's orbit so q happens at 40° behind Earth and 69° behind Mars. This arrangement enables Habitat to rendezvous with Earth 51 days after q; 67 days after Earth, it could rendezvous with Mars.

IT TURNS OUT that such a rendezvous would be rare for Earth, because this same configuration would seldom repeat.

However, orbital resonance enables Habitat to rendezvous with Mars at same position for every orbital cycle.

**Selected Orbital Elements**
	Orbital Period	Semimajor Axis	Semilatus Rectum	Semiminor Axis	Focus	Eccen- tricity	Angular Positions
Object	T	a	ℓ	b	c	e	Θ_i	Θ_i+1
Earth (ⴲ)	1.00 Yrs	1.000 AU	1.00 AU	1.000 AU	0.017 AU	0.0167	TBD	TBD
Habitat (H)	1.88 Yrs	1.523 AU	1.00 AU	1.234 AU	0.896 AU	0.586	0°	1°
Mars (♂)	1.88 Yrs	1.523 AU	1.51AU	1.516 AU	0.142 AU	0.0933	TBD	TBD
Given	Observed	∛(T²)	b² ÷ a	√(ℓ×a)	√(a²-b²)	c ÷ a	Given

MARS CYCLER VELOCITIES RANGE FROM 12 TO 47 KPS.

① At Θ = 0°, Habitat is at perihelion (q), nearest to Sol. Earth leads habitat by 40.16° and Mars leads by 68.60°. ② At Θ = 45°, all three objects (Habitat, Earth, Mars) have advanced, but the fast moving Habitat has gained on the other two. ③ At Θ = 90°, Habitat will cross orbit of Earth, because Habitat's orbit is designed that way. Diagrams shows a rendezvous with Earth for this particular orbit; unfortunately, Habitat orbit does not resonate with orbit of Earth, and this fortuitous event will be relatively rare. Fortunately, travelers will use "parking orbits (described later) to complete most transits to/from Earth. ④ At Θ = 129°, Habitat completes rendezvous with Mars. Since Habitat's orbit is designed with same period (T) as orbit of Mars, Cycling habitat (cycler) will rendezvous with Mars in same position for subsequent orbits; thus, travelers can count on this Habitat for consistent transport to/from Mars. ⑤ At Θ = 180°, Habitat's semi-orbit is at farthest point from Sol, perihelion (Q). Mars is far away, and Earth has almost completed a full orbit (almost a year) since the first position on the diagram.

MARS CYCLER VELOCITIES RANGE FROM 12 TO 47 KPS.

① At Θ = 0°, Habitat is at perihelion (q), nearest to Sol. Earth leads habitat by 40.16° and Mars leads by 68.60°.
② At Θ = 45°, all three objects (Habitat, Earth, Mars) have advanced, but the fast moving Habitat has gained on the other two.
③ At Θ = 90°, Habitat will cross orbit of Earth, because Habitat's orbit is designed that way. Diagrams shows a rendezvous with Earth for this particular orbit; unfortunately, Habitat orbit does not resonate with orbit of Earth, and this fortuitous event will be relatively rare. Fortunately, travelers will use "parking orbits (described later) to complete most transits to/from Earth.
④ At Θ = 129°, Habitat completes rendezvous with Mars. Since Habitat's orbit is designed with same period (T) as orbit of Mars, Cycling habitat (cycler) will rendezvous with Mars in same position for subsequent orbits; thus, travelers can count on this Habitat for consistent transport to/from Mars.
⑤ At Θ = 180°, Habitat's semi-orbit is at farthest point from Sol, perihelion (Q). Mars is far away, and Earth has almost completed a full orbit (almost a year) since the first position on the diagram.

H A B I T A T

Earth

Mars

Ang. Pos.

Radius

X-Coord

Y-Coord

Incr. Distance

Ave. Velocity

Incr. Time

Ang. Pos.

Θ_i

Θ_i+1

R_i

X_i

Y_i

Δd

V_Ave

Δt

Θ_i

Θ_i+1

Θ_i

Θ_i+1

0°

1°

0.630 AU

0.63 AU

0.00 AU

0.0110 AU = 1,646,197 km

47.24 km/sec

0.40 day

40.16°

40.56°

68.60°

68.81°

45°

46°

0.707 AU

0.50 AU

0.0128 AU = 1,916,977 km

43.75 km/sec

0.51 day

59.53°

60.03°

78.90°

79.17°

90°

91°

1.000 AU

0.00 AU

1.00 AU

0.0204 AU = 3,045,924 km

34.26 km/sec

1.01 day

90.86°

91.87°

95.56°

96.09°

129°

130°

1.584 AU

-1.00 AU

1.23 AU

0.0339 AU = 5,070,645 km

23.183 km/sec

2.53 day

154.20°

156.76°

129.23°

130.59°

180°

181°

2.416 AU

-2.416 AU

0.00 AU

0.0422 AU = 6,307,907 km

12.33 km/sec

5.92 day

20.31°

26.14°

249.44°

252.55°

Given

ℓ

1+e×Cosθ

R × Cos(θ)

R × Sin(θ)

ΔX = X_i+1 - X_i
ΔY = Y_i+1 - Y_i
Δd = √[(Δx)²+(Δy)²]

V_i	=	√[	μ_Sol	(	2 R_i	-		1 a	)]

V_Ave= (V_i+V_i+1)/2

Δd_km V_Ave	×	day 86,400sec

Given

Θ_i
+
ω_ⴲ×Δt

Given

Θ_i
+
ω_♂×Δt

Radius readily computed from Sol to Habitat; then, translate into 2 Dimensional (X.Y) coordinates.

Pythagorean Theorem helps determine incremental distances between selected pairs of positions.

Determine average velocity for each positional pair; divide distance by V_Ave for approximate travel times.

Assume Earth's
angular velocity
ω_ⴲ=360°/365.25 day
ω_ⴲ= 0.986°/day

Assume Mars's
angular velocity
ω_♂ =360°/686.67day
ω_♂ = 0.524°/day

Once each year, Earth bound residents can
observe Sol crossing the First Point of Aries (♈);
this event is commonly known as the Vernal Equinox.

Throughout each year, date indicates position.

Design Habitat orbit to have same semimajor axis as orbit of Mars; thus, both share same orbital period (1.88 year) which exceeds Earth's orbital period (1 year).

Thus, Earth will repeat much of its orbit while Mars and Habitat complete their respective orbits. Thus, using Earth dates to track progress of Habitat can result in ambiguities. Clarify by labeling Earth positions with both date and year.

However, positions of Mars/Habitat are not ambiguous; thus, they can be clearly marked with Earth date and days of travel (time since Habitat's perihelion, q).

HABITAT				EARTH				MARS
Ang. Pos.	Incr. Time	Cum. Time	Date	Ang. Pos.	Radius	Coordinates		Ang. Pos.	Radius	Coordinates
Θ_H	Δt	T	Mon-Dy	Θ_ⴲ	R_ⴲ	X_ⴲ	Y_ⴲ	Θ_♂	R_♂	X_♂	Y_♂
0°	0.40 day	0.40 day	Y-1: Aug 1	40.16°	1.00 AU	0.76 AU	0.64 AU	68.60°	1.461 AU	0.53 AU	1.36 AU
1°	0.40 day	0.81 day	Y-1: Aug 1	40.56°	1.00 AU	0.76 AU	0.65 AU	68.81°	1.461 AU	0.53 AU	1.36 AU
2°	0.40 day	1.21 day	Y-1: Aug 2	40.96°	1.00 AU	0.76 AU	0.66 AU	69.02°	1.461 AU	0.52 AU	1.36 AU
...	...	...	...	...	...	...	...	...	...	...	...
129°	2.53 day	115.70 day	Y-1: Nov 25	154.20°	1.00 AU	-0.90 AU	0.44 AU	129.23°	1.605 AU	-1.02 AU	1.24 AU
...	...	...	...	...	...	...	...	...	...	...	...
180°	5.92 day	345.11 day	Y-1: Jul 12	20.31°	1.00 AU	0.94 AU	0.35 AU	249.44°	1.562 AU	-0.55 AU	-1.46 AU
...	...	...	...	...	...	...	...	...	...	...	...
231°	2.56 day	571.84 day	Y-2: Feb 24	243.78°	1.00 AU	-0.44 AU	-0.90 AU	8.26°	1.383 AU	-1.37 AU	0.20 AU
...	...	...	...	...	...	...	...	...	...	...	...
358°	0.40 day	685.85 day	Y-2: Jun 18	356.15°	1.00 AU	1.00 AU	-0.07 AU	68.00°	1.459 AU	0.55 AU	1.35 AU
359°	0.40 day	686.25 day	Y-2: Jun 18	356.55°	1.00 AU	1.00 AU	-0.06 AU	68.21°	1.460 AU	0.54 AU	1.36 AU
360°	0.40 day	686.65 day	Y-2: Jun 19	356.94°	1.00 AU	1.00 AU	-0.05 AU	68.42°	1.460 AU	0.54 AU	1.36 AU
Given	Prev Table	ΣΔt_i	Convert T	Θ_i-1 + ω_ⴲ×Δt	ℓ_ⴲ 1+e×Cos(θ)	R_ⴲCos(θ_ⴲ)	R_ⴲSin(θ_ⴲ)	Θ_i-1 + ω_♂×Δt	ℓ_♂ 1+e×Cos(θ_♂)	R_♂Cos(θ_♂)	R_♂Sin(θ_♂)

CONCLUSION
For Habitats to routine travel to/from Earth, humanity must complement above "Marsonance" orbit.
Brainstorm produces following ideas; some will be further considered in subsequent chapters.

**Multiple Marsonance** orbits; increase odds of Earth proximity during Earth orbit intercepts.

**Parking orbits:** for some intercepts, Habitat can launch smaller vessel to "park" in slightly smaller/larger orbit which slowly approaches Earth.

**Multiple Earth Resonant** orbits (period is multiple of Earth's orbit, 1 year) to increase odds of Mars proximity during Mars orbit intercepts.
HABITAT ORBIT STARTS
	Reference Ray (Θ =0°) extends from Sol to q, Habitat's perihelion. For this Habitat, our Cycler, to rendezvous with Earth and Mars, orbit requires indicated lead angles; thus, when Habitat is at Θ =0°: Earth leads Habitat by about 40°. Since Habitat is closer to Sol and quicker in this part of the orbit, it intercepts Earth in 51 days for this particular orbit. Mars leads by approximately 69°. 116 days later, Habitat intercepts Mars as well as for subsequent orbits. With same period as Mars, Cycler consistently lags the "Red Planet" by same angle (69°) at every "q". However, Earth's lead angle is inconsistent and does not lend itself to repeating rendezvous.
HABITAT INTERCEPTS MARS ORBIT (Twice!)
② 1st Intercept: 116 days after q (Θ=0°), Habitat will rendezvous with Mars. ③ Habitat's position at 231 days is Θ=159° after q. ④ Aphelion. 345 days (Θ=180°) into orbit, Habitat reaches farthest point from Sol, also the orbit's slowest point. ⑤ Habitat's position at459 days ; Θ=201° past q. ⑥ 2nd Intercept: 574 days (Θ=231°), Habitat again intercepts orbit of Mars; however, Mars, the planet, is far away and out of sight.		Future Intercepts Since Cycler orbit has same period as Mars orbit, it will continue future Mars rendezvous at same position. With regards to q, both orbital intersections will continue at same angles: 129° and 231°. same travel times: 116 and 574 days.
Consider Earth Intercepts During First Orbit.
Traditionally, q, orbit's perihelion, is an orbit's starting point. For the first orbit, we arbitrarily start this orbit at August 1, which puts Earth leading Habitat by 40°. Furthermore, we arbitrarily place Mars leading by 69°. Earth's initial position enables rapid rendezvous with Earth after 51 days of orbit from q.	From Earth, Habitat needs 65 days to travel on to Mars. *ALTERNATE SCENARIO:* Habitat could launch from Earth when Mars-Earth are in Sep 22 positions.) Habitat orbital period (686 days) greatly exceeds period of Earth orbit. Thus, clarity requires Earth positions to label with both date and year. At Mar 22 (Yr2), Earth reaches 2nd possible intercept point. This is over a year (476 days) since the Mars rendezvous. .	Habitat completes an entire orbit in 686 days (Jun 19, Yr2); then, it starts another orbit. Fortunately, Mars once again leads by 69°. Unfortunately, Earth no longer leads by 40°; instead it now lags q by 3°. Thus, habitat's 2nd orbit will likely not intercept Earth in same way. Forty-one days later (Apr 28), Habitat reaches same position. Thus, intercept not accomplished.
Consider Habitat's Subsequent Orbits.
① Start 2nd Orbit 686 days after start of first orbit. Earth slips from a lead of 40° to a lag of -3°, but Mars maintains lead of 69°. ② 51 days later, Habitat intercepts orbit of Earth but not Earth. Earth arrives at this point 44 days later. ③ 65 days later, Habitat again transits Mars. ④ Aphelion, orbit's farthest point from Sol is also orbits slowest point. Positions of Earth/Mars not shown, but be assured they are both far away. ⑤ Habitat approaches Earth, coincidental. ⑥ 2nd Orbit Ends with Earth slipping another 43° behind. We observe a trend of Earth increasing its lag of 43° per orbit; thus, we conclude that this orbit will not facilitate constant rendezvous with Earth.