INTERSTELLAR SUPER G

If g-force is great, is super g-force even greater?

---

Expectations continually adjust to ever higher levels. For example, it's very possible that someone will become a dot com billionaire; you'd think she'd be happy forever. However, relevant experience indicates such happiness lasts for a much shorter time.

---

Our billionairess will soon learn that a billion dollars is not infinite, and materialistic desires will quickly grow to accommodate that finite amount. For instance, she can fly her private jet; but she now dreams of space travel.

---

In similar fashion, consistent g-force propulsion will prove a great boon to interstellar travelers as g-force propulsion will reduce interstellar voyage durations from centuries to years.  However, humans will soon want even faster transport for much quicker cargo deliveries. Interstellar shipments of essential materials could be greatly expedited if they could fly at super-g.

---

See associated 7G TABLE: Accelerate for 100 Days.

---

Near Earth's surface, a free falling object will accelerate at rate g, approx. 9.8 m/sec2. Thus, an acceleration of 10 g would be about 98.1 m/sec2. Using Newtonian motion equations, we previously determined the first second of 1-g free fall will move object 4.9 meters. Extend  to one day of constant g-force acceleration to move vessel to .245 Astronomical Units (AUs).	Expand our thought experiment's envelope to exceed g-force acceleration for selected vessels. Assume no humans, but Artificial Intelligence (AI) devices will guide a vessel with essential cargo. Express 10g differently. 10g ≈ 98.065 m sec2 × (86,400 sec)2 day2 × 1 AU 149,597,870,700 m ≈ 10g ≈ 4.893 AU day2 If double g-force does not damage ship or contents; then, much shorter travel time would be an enormous benefit.   d = a×t2 2 ≈ 4.893 AU day2 × (1 day)2 2 = 2.45 AU let a = 10g = 4.893 AU/day² NOTE: 1 sec of 10-g acceleration moves an object 49.1 m; thus, extend to 1 day (86,400 sec) for distance of 2.45 AU.
First Day of i×G-force Propulsions Describe greater accelerations as integer (i) times g, gravity force experienced on Earth's surface. DISTANCE EXAMPLE:  After one day of 10g-force acceleration, object travels a great distance: dAccel = .5 × a × t2 = .5 × 10g × t2 = .5 × 10(.245AU/day2) × day2 = 2.447 AU
Attain Great Speeds with 1-G Propulsion Re-express light speed, c c = 299,792.458 km sec    = c × AU 149,597,871 km × 86,400 sec day = 173.145 AU day Daily Difference: Δ1-G = VDay c =  .489 AU/day 173.145 AU/day  =  0.283% c Daily Remainder: (1 - Δ) R1-G = c (1 - Δ1-G)  = c(1-.00283) = .99717 c Previous work shows Vt = c(1 - Rt) Time Einsteinian Velocity Newtonian Velocity Days % Light Speed AU/Day AU/Day 1 0.283% c 0.490 0.490 5 1.407% c 2.436 2450 10 2.794% c 4.838 4.900 t c (1-Rt) Convert t × a1-G Show Einsteinian velocities as both percent light speed (%c) and equivalent AUs per day. For lesser velocities, Einstein and Newton velocities are fairly close.	Much Greater Speeds with 10 G Propulsion Daily Difference for 10g propulsion Δ10G= 10× 0.283%c = 2.83%c Daily Remainder for 10g propulsion R10G = c (1 - Δ10G)  = c(1-.0283) = .9717 c For 10g propulsion, let R = .9717. Time Einsteinian Velocity Newtonian Velocity Days % Light Speed AU/Day AU/Day 1 2.830% c 4.838 4.838 5 13.371% c 23.152 24.190 10 24.955% c 43.208 48.380 t c (1-Rt) Convert t × a10G After 10 days of 10-g propulsion, Einsteinian velocity significantly differs from Newtonian velocity. TE assumes Einsteinian velocity is more accurate.  See next table.
Velocities for Different Super-G's Accel. a = 1 × g a = 4 × g a = 7 × g a = 10 × g Daily Diff. Δ = .2826%c Δ = 1.1305%c Δ = 1.9784%c Δ = 2.826%c Daily Rem. R = 99.7174% R = 98.8695% R = 98.0216% R = 97.1738% Time (t) Einstein Newton Einstein Newton Einstein Newton Einstein Newton AU/day AU/day AU/day AU/day AU/day AU/day AU/day AU/day 1 day 0.489 0.489 1.957 1.957 3.425 3.425 4.893 4.893 10 days 4.832 4.893 18.608 19.574 31.360 34.254 43.158 48.935 100 days 42.68 48.93 117.60 195.74 149.67 342.54 163.70 489.35 200 days  74.84 97.87  155.33 391.48 169.96 685.09 172.58  978.69 300 days 99.07  146.80  167.43 587.22  172.71 1,027.63 173.11  1,468.04 365¼ days  111.56  178.73 170.42  714.92   173.03 1,251.14 173.14 1,787.34 400 days  117.33 195.74 171.31 782.96  173.09 1,370.17 173.14 1,957.39 Given Vt = c × (1 - Rt) 173.145 AU/day c Einsteinian Velocities Vt = t × a = t × i×g = t × i × 0.489 AU day² Newtonian Velocities For even faster interstellar cargo transport, consider super G-forces even greater than 1g. With acceleration as i × g,  table considers integer "i" values as high as 10. Newtonian method computes velocities greater than light speed (c=173.145 AU/day) ; IMPOSSIBLE!!!! Thus, Thought Experiment proposes Einsteinian Velocities for subsequent use.
Interstellar Distances for Different Super-G's Accel. a = 1 × g a = 4 × g a = 7 × g a = 10 × g Daily Diff. Δ = .2826%c Δ = 1.1305%c Δ = 1.9784%c Δ = 2.826%c Daily Rem. R = 99.7174% R = 98.8695% R = 98.0216% R = 97.1738% Time (t) Velocity Distance Velocity Distance Velocity Distance Velocity Distance %c LY %c LY %c LY %c LY 1 day 0.28% 0.0000039 1.13% 0.0000155 1.98% 0.00003 2.83% 0.00004 10 days 2.79% 0.00038 10.75% 0.00150 18.11% 0.00256 24.93% 0.00358 100 days 24.65% 0.035 67.92% 0.110 86.44% 0.155 94.31% 0.184 200 days 43.22% 0.129 89.71% 0.332 98.16% 0.413 99.68% 0.452 300 days 57.22% 0.268 89.71% 0.589 99.75% 0.685 99.98% 0.726 365¼ days 64.43% 0.377 98.43% 0.763  99.93% 0.863 99.9972% 0.905 400 days 67.76% 0.440 98.94% 0.857 99.97% 0.958 99.9990% 0.999999 Given Vt = (1 - Rt) ×  c Einsteinian Velocities dt = c × t + Vt ln(1-Δ) Einsteinian Distances For even faster interstellar cargo transport, consider super G-forces even greater than 1g. With acceleration as i × g,  table considers integer "i" values as high as 10. Thought Experiment proposes Einsteinian Velocities and Distances.
 EXAMPLE: Let one second of consumed fuel flow, ffsec, be 1,000 gms of at rest water particles.  Accelerate these particles to a relativistic exhaust velocity ( VExh) of .992 light speed. VExh = dc×c =.992c = 99.2% light speed As shown in the right hand panel, 1.0 kg of ffsec will grow to become 8.0 kgs of exhaust fuel flow, ffExh,  just before it exits vessel and contributes to forward momentum.  NOTE:  Consume fuel particles at rest; expel at relativistic speeds. ffExh = n × ffsec	For convenience, note following identities: Growth Factor n = 1 √(1 - dc2) Growth Factor (n) Uses Lorentz Transform (LT) as shown. Decimal Component (dc) If particle speed is expressed as decimal light speed; then, dc is the decimal portion. Decimal Component dc     =  √(n2 - 1) n LT can be rewritten to solve for dc  (see table at right).  Thus, conveniently generate below table. Growth Factor (n) 1 2 3 4 5 6 7 8 Fuel Exhaust Speed(dc×c) 0.00c .866c .942c .968c .980c .986c .990c .992c For convenience, n is expressed as series of integers, but n could also be a rational number greater than 1. To discuss following tables, TE arbitrarily assumes a relativistic growth factor of 8.
∇E=1= ffDay  MShip Determine ratio of daily fuel to Ship's Mass ∇E=1= 86,400 × ffSec  MShip Daily fuel = 86,400 seconds of at-rest fuel consumption  To determine ship's mass: Recall Momentum Exchange Huge mass of ship × small velocity increase = tiny collective mass of fuel exhaust particles × huge relativistic velocity. MShip × VShip = MExh × VExh  Divide each side by one second for useful restatement. MShip × VShip sec = MExh × VExh sec Ship's velocity per second (VShip/sec) can be expressed as ship's acceleration (AShip). Exhaust mass per second (MExh/sec) can be expressed as ship's exhaust fuel flow (ffExh).	Substitute and re-arrange: Equal Forces MShip × AShip = ffExh × (dc × c)  State ship's acceleration (AShip) as multiple of g, Earth's gravity: Equal Forces Restated MShip × (i × g )  = (n ×ffsec) × (dc × c) ∇E=1= ffDay Mship = 86,400 × ffSec n×ffSec×dc×c/(i×g) Solve for Ship's mass (Mship) and substitute: ∇E=1 = ffDay Mship = 86,400 ×i×g/c n × dc Further simplify: n × dc = n × √(n2 - 1) n = √(n2 - 1) Recall decimal component in terms of n, growth factor: ∇E=1 = i×.2826% GW √(n2-1) Make following substitutions: Light speed, c = 299,792,458  m/sec Earth gravity, g = 9.8065 m/sec² ∇E=1 = i × .0356% GW Make following substitutions: Growth factor, n = 8 √(n2-1) = 7.937 Gravity Mult (i) 1 2 3 4 5 6 7 8 Exhaust Flow (∇) 0.0356% 0.0712% 0.1068% 0.1424% 0.1780% 0.2136% 0.2492% 0.2848% If perfectly efficient vessels were possible; then, a 7g-force vessel could use 1% of it's GW for 4 days propulsion. However, we must also consider INEVITABLE INEFFICIENCIES!! TE proposes a coefficient {efficiency factor (ε)} to increase fuel consumption (∇ ) to cover both the Exhaust Flow (ffExh=n×ffsec) and inevitable particle losses: design flaws and peripheral systems.
Synchrotronic Propulsion System will have inevitable inefficiencies. However, they will improve over time.	Inefficiency  (E'= loss/input) reflects the inevitable loss of consumed fuel particles which will not exit the vessel to contribute to ship's velocity increase.  This loss may be intentional such as particles diverted for other services.  Loss may be unintentional due to design flaws.  TE assumes that subsequent designs will decrease particle loss. Interplanetary Inefficiency: TE assumes  50%. Interstellar Efficiency must be much better than interplanetary; thus, TE assumes constant tech improvement correlating to n, growth factor. (For following examples, let n = 8.) E' = (.5 × .9n-2) = .2657  Efficiency, E, can be stated as complement of Inefficiency, E'. E =  1 - E' = 1 - (.5×.9n-2) = .7347  Efficiency Factor (ε) is a necessary coefficient of daily exhaust flow (∇).  As the reciprocal of Efficiency, ε always exceeds one: ε = 1 1 - (.5×.9n-2) = 1.362
Interstellar Daily Difference Efficiency Factor (ε) helps flight planners account for inevitable inefficiencies. Gravity Mult (i) 1 2 3 4 5 6 7 8 9 10 Daily Diff. (ε×∇) 0.0468% 0.0936% 0.1404% 0.1872% 0.1872% 0.2808% 0.3276% 0.3744% 0.4212% 0.4680% Given 7g acceleration, 1% ship's gross weight will provide about 3 day's propulsion. Interstellar Fuel Consumption for G and Super-G Accel. a = 1 × g a = 7 × g Daily Diff. ε∇ = .0468% GW ε∇ = .339% GW Daily Rem. (1-ε∇) = 99.9532% GW (1-ε∇) = 99.61% GW Time (t) Velocity (Vt) Distance (dt) Fuel (ft) Velocity (Vt) Distance (dt)  Fuel (ft) percent c Light Year percent GW  % light speed Light Year %Gross Wt. 1 day 0.28%c 0.000 003 9 LY  0.048% GW  1.98%c 0.000 03LY  0.339% GW 10 days  2.79%c 0.000 38 LY  0.48% GW  18.11%c 0.002 56LY 3.34%  GW 100 days  24.65%c 0.035 LY  4.73%GW 86.44%c 0.155LY 28.82%GW 200 days  43.22%c 0.129 LY 9.24%GW 98.16%c 0.413LY 49.34%GW 300 days  57.22%c 0.268 LY 13.54%GW 99.75%c 0.685LY 63.94%GW 365¼ days   64.43%c 0.377 LY  16.23 %GW 99.93%c 0.863LY 71.11%GW 400 days   67.76%c 0.440 LY   17.63%GW 99.97%c 0.958LY 74.33%GW Given Vt = c × ( 1 - (1-Δ)t ) Einsteinian Velocities dt = c × t + Vt ln(1-Δ) Einsteinian Distances ft = 1 - (1-ε∇)t Fuel Consumed For even faster interstellar cargo transport, consider 7g acceleration. Assume fuel exhaust particles have velocity, VExh = 99.2%c, with a corresponding growth factor, n = 7. Thought Experiment proposes Einsteinian motions and exponential fuels.
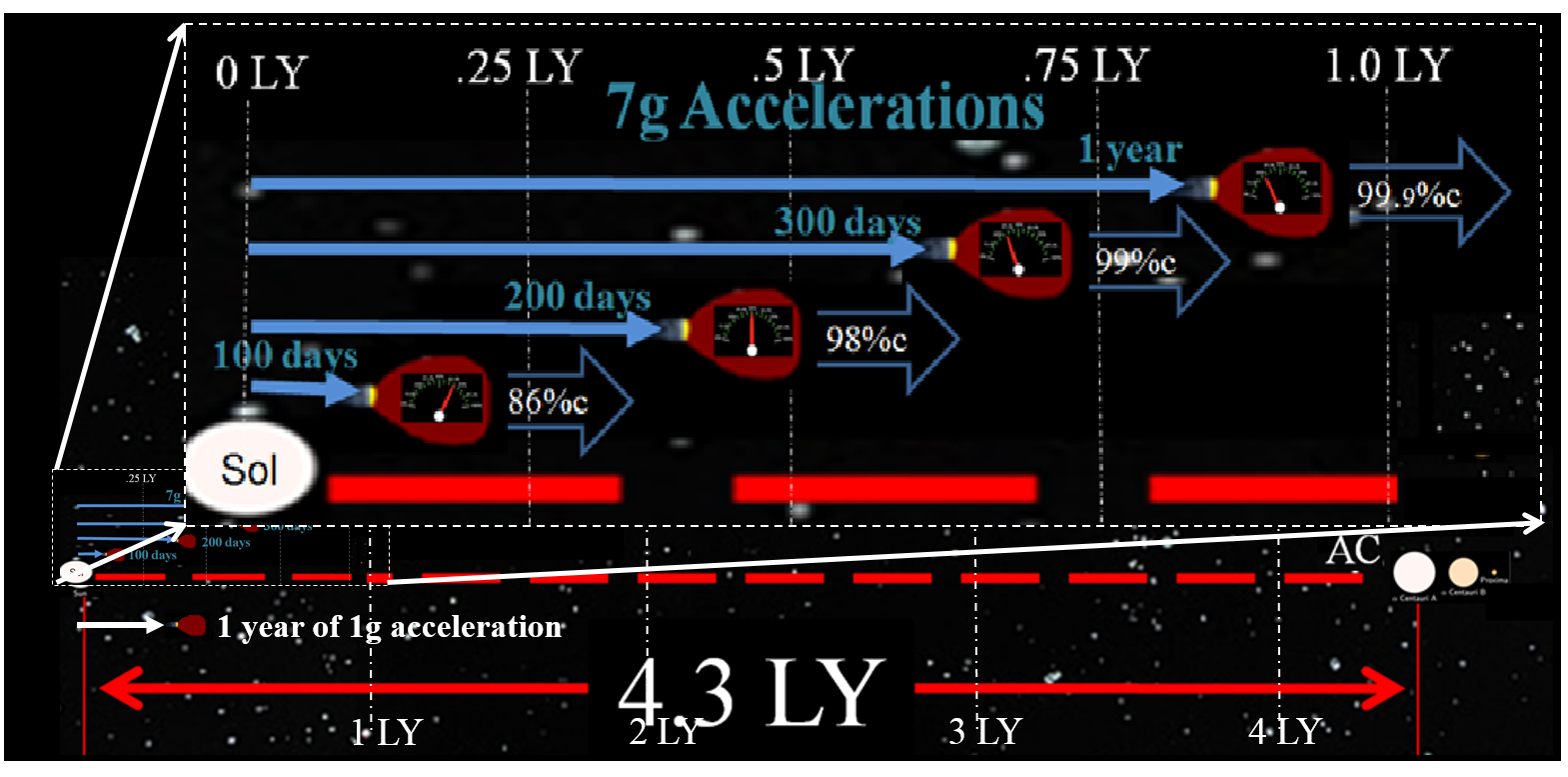7g acceleration greatly increases distance and speed much quicker than 1g acceleration; DOWNSIDE:  7g propulsion requires MUCH MORE FUEL!!! For more, see "Snowball from Oort".

SLIDESHOW

---

---

---

---

VOLUME 0: ELEVATIONAL
VOLUME I: ASTEROIDAL
VOLUME II: INTERPLANETARY
VOLUME III: INTERSTELLAR

---

---

---

---