Sunday, February 10, 2013

FINITE FUEL

   
One tank of gas
can only take your car so far.
Like your car, thought experiment's
spaceship has a finite range.
Recall basic principle of rocket propulsion, many high speed particles exit the aft end to form the Propulsion Vector as shown. Thought Experiment (TE) proposes "g-force" propulsion where a specified quantity of charged particles exit aft end at near light speeds. For each second of powered flight, subsequent momentum exchange increases ship's velocity about 10 meters per second (recall that acceleration due to gravity at Earth's surface is about 10 m per second per second (10 m/s²)). Ship's passengers would feel Earth like gravity (Einstein's "Equivalence"), and ship's speed would increase very quickly.
Total quantity of particles expelled per second might be on the order of kilograms, and the vessel might be 100,000 metric Tonnes (mTs), about the size of a modern naval, aircraft carrier.  This constant particle expulsion will significantly reduce the vessel's mass.  If vessel's power system consumed 1 kg/sec, the vessel's  Gross Weight (GW) would decrease by 864 mTs for that day. However, the decreasing GW means the fuel consumption is also decreasing.
We can determine the g-force vessel's decreasing daily decrement as a percentage.
Due to momentum exchange, high speed exhaust particles propel the much bigger rocket in the opposite direction for a slight speed increase. Momentums fore and aft are equal and can be described by following equation:
Eq-1:
ffExh × vExh = MShip × g
Our thought experiment increases the spaceship's speed 10 m/sec for each second of powered flight.  This speed increase approximates g, free fall acceleration near Earth.
To get the required momentum from the exhaust particles, ffExh, our thought experiment proposes a particle accelerator as the propulsion system for our notional spaceship. Accelerator brings the particles to relativistic speeds, vExh, which gives exhaust particles extremely high speeds (fractional light speed) as well as increased mass due to relativistic effects.
Thus, this notional, accelerating spaceship travels to nearby planets in days, much quicker than the many months required for orbiting spacecraft. Another benefit: constant, consistent acceleration "presses" the spacecraft structure against the passengers, crew and payload to produce the same g-force feeling as if standing on Mother Earth (Einstein's "equivalence"). Thus, g-force powered spaceflight simulates gravity.
Ship's propulsion system accelerates a predetermined mass of ionized particles (plasma) to exit vehicle at relativistic speeds. Since these ions come from designated, onboard material, this material fuels the spaceship much like gasoline fuels our automobiles. For both vehicles, when we add fuel, the total gross weight (GW) increases; when fuel transforms into energy to produce motion, fuel is consumed, and Daily Gross Weight (GWDay) ever decreases as vessel consumes fuel.  If we know the initial fuel load and the consumption rate; then, we can calculate the time required to consume available fuel, the ship's range.
Note Following Assumptions
1) Inevitable inefficiency enables us to introduce some practicality into this model.  Previous work introduced the term, ε (Greek "epsilon") as an efficiency factor.  Examples:  To artificially represent the unachievable 100% efficiency for fuel flow conversions, ε would equal 1.0.  For the Thought Experiment (TE) model, we choose a much more practical 10% fuel flow efficiency; thus,
ε = 10% = 0.1 
Someday, actual empirical data will determine actual efficiency factors.
2) Marginal Fuel Requirements - it makes sense to plan for "spare fuel"; it's always a good policy to plan the mission to end with some fuel remaining. Since this fuel is not planned for consumption, it might be better to consider marginal fuel as part of ship's infrastructure. Thus, thought experiment disregards spare fuel for computing range of spacecraft.
3) Assume continuous g-force acceleration due to constant particle exhaust; TE calls this "powered flight" in contrast to orbiting, spinning habitats which are traveling in "non-powered flights".
  • TABLE-1 assumes exhaust speed, vExh = 27.3% light speed (c).
  • TABLE-2 assumes greater exhaust speed, vExh = 86.6% c.
  • TABLE-3 considers several even greater exhaust speeds.
Rearrange Equation 1 (Eq-1):
Eq-2:
MShip=ffExh × vExh
g
Recall previous work:
Particle exhaust speed, vExh, can be described as decimal light speed: dcc
c
is light speed
dc
is decimal component
Example: Let vExh = .27c ; thus, dc = .27
Exhaust particle mass, ffExh, will be larger then originally consumed fuel, ffSec, due to relativistic growth. This growth factor can be determined by Lorentz Transform (LT) which determines relativistic mass increase, mr.
mr= 1
√(1-dc2)		=1
√(1-.272)		= 1.04
Exhaust particles with velocity of .27c will grow 4% due to relativity.
ffExh = mr × ffsec= 1.04 × ffsec
Thus, Equation 2 (Eq-2) can be rewritten:
Eq-3:
MShip=
mrffsec × dcc
g
Recall fuel flow per second (ffsec) is the quantity of at rest fuel consumed per second; however, typical g-force flight durations can be reckoned in days.  Accordingly, TE determines daily fuel consumption. Thus, let DaySec = 86,400 seconds per day; then, typical day's fuel consumption can be described as:
FDay = DaySec × ffsec
TE now introduces a new term, Percent Take-Off Gross Weight for first day of powered flight, %TOGWDay1.  Simple substitutions and rearrangements give us Equation 4 (Eq-4).
Eq-4:
%TOGWDay1= FDay
MShip		=DaySec × ffsec
mrffsec × dcc÷g 		=g × DaySec
c × (mr×dc)
COMBINE CONSTANTS:
c (light speed), g (acceleration due to Earth surface gravity),
and DaySec (seconds per day) are shown below:
g × DaySec
c		= 9.8065 m/s2×86,400sec/day
299,792,458 m/s		=0.2826%
day
From Lorenz Transform,
Recall relativity growth factor, mr:
mr= 1
√(1-dc2)
Rewrite expression for mr,
to solve for decimal component of light speed, dc:
dc= √(mr2-1)
mr
Rewrite expression, mr×dc:
Eq-5:
mr×dc= mr× √(mr2 -1)
mr		=
√(mr2-1)
Eq-6 Determines Daily Difference in Gross Weight
%GWDay is daily percent decrease of vessel's GW.
NOTE:  Vessel's GW ever decreases
due to fuel consumption;
however, daily percentage of GW
used for fuel remains constant. 
Eq-6:
%GWDay  = g × DaySec
c × √(mr2 -1) 		= 0.2826%/dy
√(1.042-1)		=1%/day
Work gives us following points:
  • With exhaust particles at 27% light speed (dc  = .27),  relativism grows exhaust particles by 4% (thus, mr = 1.04).
  • With this speed and mass,  1% of ship's GW can propel a 100% fuel efficient vessel for one day of constant g-force (Eq-6 disregards practical factors such as design learning curves and peripheral power needs, and artificially assume 100% efficiency in converting fuel to propulsion.  Following Eq-7 introduces some practicality.)
Practical Daily Difference  (Δ)
INTRODUCE SOME PRACTICALITY:
Use Efficiency Factor (ε)
to account for inevitable inefficiencies.
For this example,
assume 10% fuel efficiency;
thus, let ε = 1/E = 1/10% = 10
Eq-7:
Δ = %GWDay
E 		= 1%/dy
.1		=10% GW/day
Thus, we can conclude that ships Gross Weight (GW) decreases certain percentage for every day of g-force propulsion.  This daily difference, Δ, depends on particle's exhaust speed and fuel conversion efficiency. Following show that Δ and logarithms can give us a gracefully model g-force vessel's ever decreasing GW.
Apply Rate
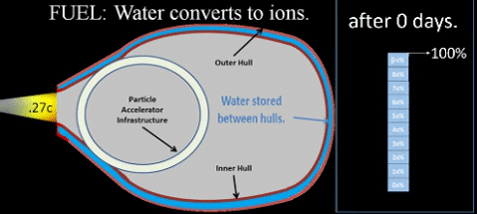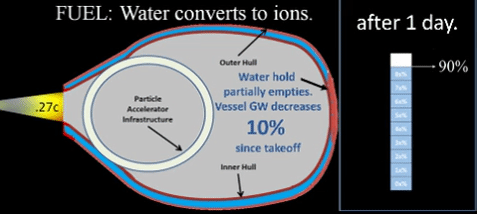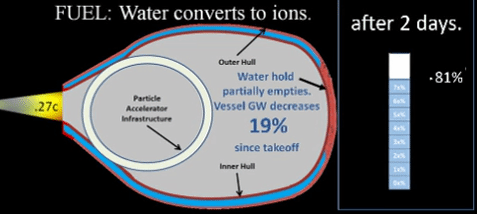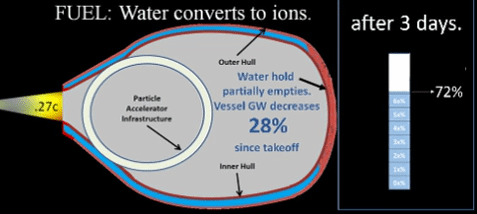
If ship's initial gross weight (GW0) is 100 metric Tonnes (mT); then, ship will consume 10 mTs of fuel on first day of powered flight.
FDay = Δ × GW0 = 10% × 100mT = 10mT
GW1 = GW0 - FDay = 100mT - 10mT = 90mT
Assume we devote half of ship's mass to fuel; (%TOGW = 50%). Then, ship starts with 50 tons of fuel, and a rate of 10%/day seems to give us 5 days of powered flight. Thus, 5 days can be an initial approximation of ship's range.
Fortunately, ship's actual range is slightly better.
At beginning of trip, no fuel is consumed.
Day 0Initial Weight =GW0=TOGW=100 mT
Thus, the initial value of FDay ( = Δ × GW0) is really only good for first day of flight. After the first day, GW decreases due to fuel consumption. Thus, Δ is a dynamic daily percentage value, and it reflects the ever decreasing GW during powered flight. For convenience, let daily decrement be ten percent of ship's Gross Weight (10% = .10).
1st day of trip, fuel consumption; Δ = 10% ×GW0= 10 mT.
Thus, GW1 = GW0 - first day's fuel consumption.
Day 1GW0  × (1-Δ) =GW1=100mT × .9=90 mT
2nd day, ship consumes 10% of GW1; Δ = 10% ×90 mT = 9 mT.
Thus, 2nd day's fuel consumption is less then 1st day's.
Furthermore, GW at end of day 2 (GW2) is less than GW1 at end of day 1.
Day 2GW0  × (1-Δ)2=GW2=100mT × .92=81 mT
3rd day, fuel consumption will be even less and so on as shown in following table.
Day 3GW0  × (1-Δ)3=GW3=100mT × .93=72.09 mT
100mT × .9 × .9 ×.9 =GW3=GW0 (1-Δ)3
Day tGW0 × (1-Δ)t=GWt=100mT × .9t<<100 mT
To determine ship's gross weight (GW) for any given day "t" (GWt), multiply original quantity (GWo), by initial daily decrement "(1-Δ)" raised to the power "t".
Eq-8:
GWt    = GW0 × (1-Δ)t
Exponentials
We see that exponentials can readily approximate fuel consumption. Any inexpensive scientific calculator has an exponent function; thus, we can readily calculate numerous guesses as to how many days is required to reduce ship's original gross weight (GW0) by 50%.Our initial intuituive guess was 5 days; recall it seemed that 50 mTs divided by 1- mT/day might give us 5 days of powered flight.
Divide %TOGW by first day's Δ: (50 mT/10 mT/day = 5 days)
However, our guess fails to consider that ship's GW decrements by percent not by absolute weight. Consider that as fuel is consumed, GW declines; a lesser GW needs less fuel to propel it, and this cycle continues throughout powered flight (as shown by above table). Thus, mass of fuel consumed decreases throughout flight even though the percentage of GWDay remains the same.
Let Δ = 10%; then, 1-Δ = 90% = .9
A quick exponential calculation shows that 5 days of 10% consumption only reduces ship's gross weight to about 60% GW0.
.95 = .5905 = 59.05%
Day 5GW0×(1-Δ)5=GW5=100mT×.95=59.05 mT
However, we want to determine time (t) for GWt = 50%;
thus, we might test several t values:
.9t = 50% GW0
to eventually determine a t value for a GW near 50%.
Thus, we determine that at 10% GW consumption per day; 6.6 days takes us very close to 50% of
original mass.
Day 6.6GW0×(1-Δ)t=GW6.6=100mT×.96.6=49.88 mT
Thus, a daily difference (Δ) of 10%/day gives our notional spaceship a range of about 6 and a half days of powered flight.
There might be a more graceful way to determine this range. 
Logarithms
Use logarithms to readily compute accurate ranges.
A quick review of base 10 logarithms follows:
log10a = a
Obvious Example-1, log(100) = log(102) = 2
Subtle Example-2, log(70) = log(101.845) = 1.845
What if at = b, where a and b are known, but t is unknown?
Exponential characteristics allow us to accomplish following:
at=b
log(at)=log(b)
t × log(a)=log(b)
t=log(b) / log(a)
For present case, substitute following terms:
(1 - Δ)t=1 - %TOGW
log(1 - Δ)t=log(1 - %TOGW)
t × log(1 - Δ)=log(1 - %TOGW)
Eq-9:
t=
log(1 - %TOGW)
log(1 - Δ)
For present case, use following values:
Daily Decrement: Δ = 10%; thus, 1-Δ= .90.
Percent Take-Off Gross Weight is 50%; thus, 1-%TOGW = .5000
.90t=.5000
t=log .5000 / log .90
t=-.301/ (-.04576)
t=6.58
Thus, logarithms can quickly approximate ranges for different values of %TOGW.

TABLE-1. Fast Particles

Particle Exhaust Speed is 27% c (light speed) 
Relativistic speed increases mass by 4% (mr = 1.04)
Arbitrarily assume propulsion efficiency, E = 10%; thus, ε=1/E=10
then, g-force fuel consumption = 10% GW per day = Δ (daily difference).
Original
Fuel
Load
Final
Gross
Weight
Decimal
Light
Speed**
Relativistic
Mass
Increase**
Gross Wt
Daily
Difference**
G-force
Vessel
Range
F0GWFindcmrΔRDays
(%TOGW0)(%GW0)(dc c)
(%GW)(days)
10%90%.27 c1.0410%1.00
20%80%.27 c1.0410%2.12
30%70%.27 c1.0410%3.39
..................
40%60%.27 c1.0410%4.85
50%50%.27 c1.0410%6.58
60%40%.27 c1.0410%8.70
70%30%.27 c1.0410%11.43
80%20%.27 c1.0410%15.28
90%10%.27 c1.0410%21.85
Indep.
Variable		1-%F0Given1
√(1-dc2)		ε × .282%
√(mr2-1)		log(%GWFin)
log(1-Δ)
Range (RDays) is total days of completed flight time.
Gross Weight (GWt) is ship's gross weight (GW) after t days of flight.
Original Gross Weight (GW0) is ship's gross weight after zero days of flight. It includes ship structure, payload, passengers, crew and original fuel, F0.
GWt = GW0(1-Δ)t
F0 , is fuel mass needed to power spacecraft through entire flight. This includes departure leg & return leg. Since spare fuel is not planned to burn, TE considers it part of the ship's infrastructure and not part of F0.
Transition to TABLE-2
Fewer Columns. Several TABLE-1 columns have static values.**
Thus, TABLE-2 deletes these columns and lists relevant values only once in header.
is the amount of fuel required for entire mission.
This value is expressed as a percentage of the vessels' initial gross weight, GW0.
%GW0= F0/GW0
Final Gross Weight (GWFin) is remaining gross weight after fuel depletion.
GWFin = GW0 - F0
GWFin can be expressed as a percentage of GW0.
GWFin =
(GW0 - F0) ÷ GW0
GWFin =
1 - %GW0


Δ = ε×0.2826% /day
√(mr2-1)
Daily Difference (Δ)
is percentage amount that ship's GW decreases per day.
Efficiency Factor (ε) helps account for design flaws and peripheral power needs.
Δ is expressed as percentage of gross weight, GW.
RDays =log(1-%TOGW)
log(1-Δ)
Vessel Range (RDays)
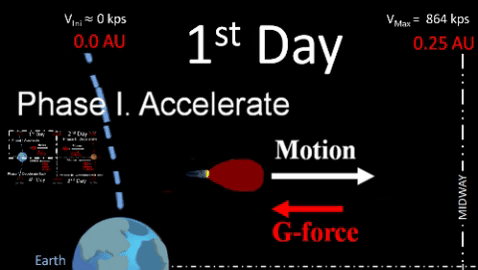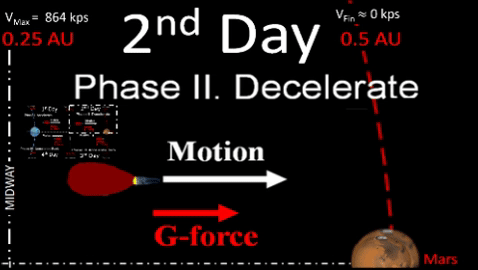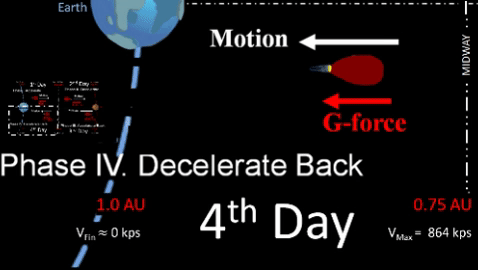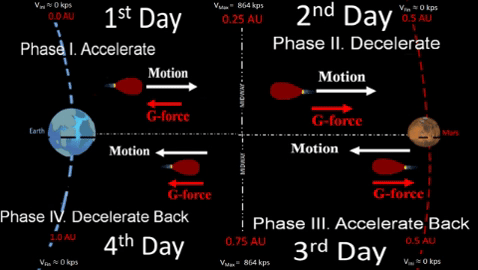
is total days of powered flight available from original fuel load.
Following four phases of interplanetary travel must fit within.
Flight Profile Assumptions
  • Acceleration Time: Let tAcc = time to accelerate from departure to half the distance to destination (midway). We assume continuous g-force from start to midway.
  • Deceleration Time. Let tDec = time to decelerate from midway to destination.  Since we're both accelerating and decelerating at g-force, we assume that deceleration time = acceleration time:
     tDec = tAcc
  • Requisite Flight Profile. Since g-force trip times take only days (versus months for non-g-force flights), we further assume nearly same distances for both legs (departure and return); thus, we further assume time to travel departure leg is same as time for return leg:
    tAcc + tDec = tDept = tRetn = tDec + tAcc
Flight profile has 4 phases of same duration:
Example: Diagram shows all phases with 1 day duration.
However, phases can be determined for any interplanetary distance (1 to 100 AU).
  • Departure Leg can split into two equal phases:
    • Phase I: g-force spaceship accelerates at g from Earth to half the distance (d/2) to the destination.  Let tAcc and dAcc, be time and distance (respectively) from start of acceleration until stop of acceleration.  Thus, d/2 = dAcc .
    tAcc and dAcc have the relationship: dAcc = g × t2Acc / 2
    or solve for tAcc to get: tAcc = √(2 × dAcc / g)
    • Phase II: To accomplish the required slowdown and continue g-force from midpoint to destination, spaceship decelerates by reversing propulsion vector for same duration as for acceleration. Since vessel must decelerate for the distance, d/2: dDec = d/2 = dAcc
    • Total Time of Departure Leg. Consider it axiomatic:  tDept = tAcc + tDec = 2 × tAcc
  • Return Leg also has two equal phases. Thought Experiment (TE) assumes Return Leg distance (d) to be same distance as Departure Leg.
    • Phase III: Accelerate back from destination to midpoint; distance/time will be same as for Phase I.
    • Phase IV: Decelerate from midpoint back to Earth.  Distance/time is same as for other phases.
  • Total Trip Time, t: With some substitutions, total trip time can be described:
    • tTtl = tDept  + tDest  = 2 × tAcc + 2 × tDec = 4 × tAcc
Acceleration Time, tAcc
We've already determined range based on original fuel load, F0, (possible range in time (days) from %TOGW and GWFin; see above table).
Thus, we can divide vessel's Range (RDay) by four to determine maximum acceleration time for Phase I:
tAcc = RDay / 4
Increasing particle exhaust speed, VExh, to .866c
doubles mass of exhaust particles (ffExh = 2 × ffsec) to greatly expand spaceship's range.
Common sense compels us to continue assuming painful but practical efficiency factor, ε = .1.
Time will tell, but for now, TE assumes that for every 100 ffsec particles consumed, only 10 actually become effective propulsion particles (ffExh).  Thus, we must consume ten times more ffsec than we'd otherwise expect.

Daily Velocity Increase. Due to constant g-force acceleration, interplanetary g-force flights will take days; even this brief duration will increase spaceship's velocity to enormous values. Recall:
g ≈ 10 m
sec2		=10 m/sec
sec		×km
1,000 m		×86,400 sec
day		=864 km/sec
day
Thus, spaceship attains: 864 km/sec in one day, 1,728 km/sec after two days, etc.
v =g × t=
864 km/sec
day
× t
where t = time in days.
Flight Profile Summary.
Slowdown is required for both legs of journey: departure and return.
This is described in TABLE-2.


TABLE-2. Faster Particles

Particle Exhaust Speed: dc × c = 86.6% Light Speed.
Relativistic Exhaust Speed Doubles Mass: mr =2.
Practical Efficiency Factor: ε  = 1/ E = 1/10% = 10

Δ = ε×0.282%/day
√(mr2-1)
Δ = 10×0.282% /day
√(22-1)
Δ = 1.63%
day
%TOGW %GWFinMax
Range		Max Time
Acceleration		Max
Velocity
%GW01 - %GW0RDaytAccvMax
% % DaysDayskm/sec
5%
95%
3.14
0.79
678 kps
10%
90%
6.45
1.61
1,393 kps
20%
80%
13.7
3.43 
2,959 kps
30%
70%
21.8
5.45 
4,709 kps
40%
60%
31.0
7.75 
6,696 kps
50%
50%
42.1
 10.53
9,094 kps
F0
GW0
100%-%TOGW
log(%GWFin)
log(1-Δ)
RDay
4
tAcc × 864 km
sec
Transition to TABLE-3
Current particle accelerators now accelerate particles to velocities faster then .99c; thus, it's very likely that we'll eventually design propulsion systems to accelerate particles much faster then .866c. Thus, daily fuel consumption will decrease, and range will increase. Consider following points.
  1. ffsec For every second of flight, our notional spaceship consumes an ever decreasing quantity of "at rest" fuel which we'll call fuel flow per sec (ffsec). This is the fuel's mass prior to conversion to plasma (ions, particles with charges). Thus, fuel consumption is reckoned in terms of fuel at rest "ffsec" at zero velocity in relation to ship.
  2. ffExh For every second of flight, a particle accelerator uses a system of magnetic and electrical fields to accelerate these charged particles to large fraction of light speed. A century of particle accelerator experience confirms that ions grow as they accelerate to near light speed; thus, the consumed quantity of particles (ffsec) transform to an increased quantity ffExh, fuel flow of exhaust particles. Collective exhaust particle momentum (near light speed velocity times relativistic mass) enables spaceship's propulsion.
  3. Determine Acceleration Distance. Once we determine acceleration time, tAcc, from one fourth of the practical range (see previous work); then, we can determine acceleration distance, dAcc, as shown below.
    dAcc=g × (t²Acc)
    2
  4. Departure Distance. Determine total distance for departure leg by multiplying by 2 because deceleration distance equals acceleration distance, dDec = dAcc. This was previously discussed in Table-2. 
    dDept= 2 × dAcc
  5. 100% Efficiency is impossible for following reasons.
    • We must artificially assume every single particle makes it all the way through the many kilometers of waveguides and exits spacecraft exhaust as intended.
    • Furthermore, we must incorrectly assume no additional energy is required for other energy requirements, such as electro-magnetic fields to guide the particles.
    Thus, thought experiment arbitrarily assumes 10% efficiency for interplanetary flights because relativistic momentum provides so much capability that realistic efficiencies can be overcome. (NOTE: Interstellar flights will require much greater fuel efficiency; this will be discussed in a subsequent volume.)

TABLE-3. Even Faster

Add columns to cover increasing relativistic growth factors and associated speeds.
This table uses a constant final gross weight (GWFin) of 50% of original GW.
Relativistic
Growth		Decimal cDaily
Difference
Range
Time
Acceleration
Time
Acceleration
Distance
Total
Distance
mrdcΔttAccdAccd
%/dayDaysDaysAUAU
1.04
0.27310.0%6.971.74.7615.2
2
0.8661.63%42.4510.6128.1556.31
...
..................
3
0.9431.0%69.3417.3365.12130.25
4
0.9680.70%94.9623.74140.90281.80
5
0.9800.60%120.1330.03225.47450.94
IV√(mr2-1)
mr		ε×0.282%/dy
√(mr2-1)		log(%GWFin)
log(1-Δ)		t
4		g × (t2Acc)
2		2 × dAcc
Definitions:
  • mr is relativistic growth factor computed from Lorentz Transform.
  • dc is decimal component of particle exhaust speed when expressed as decimal light speed.
  • ε is an Efficiency Factor introduced to assure practicality of fuel requirements.  All we now know is that fuel flow efficiency will start out much less than 100%, and it will improve over time.  For convenience, Thought Experiment assumes an efficiency of 10%; thus, ε = 10.
  • Δ is the amount of at rest fuel consumed for each day's propulsion, expressed as a percentage of ship's gross weight.
  • %GWFin is the final gross weight of the spacecraft after the original fuel load fuel (%TOGW) is consumed. %GWFin is expressed as a percent of original ship's mass and can be computed: 100% -%TOGW.  Above (Table-3) uses a constant %GWFin of 50%.
  • t is total time from F0; this capacity is the range.
  • tAcc is acceleration time.
  • dAcc is acceleration distance.
  • d is total distance for departure leg. Note that this table only uses half the planned fuel for departure leg; other half is for return leg.
SUMMARY: Good News/Bad News
Good News After g-force spaceships can accelerate exhaust particles to 98% c; then 50% TOGW spaceflight profiles will have capability to accelerate for 30 days then decelerate for another 30 days to travel about 451 AUs.
Bad News In spite of this impressive feat, we've still well within our Solar System. 451 AUs is less than 1% of a light year (LY= 63,241 AU); however, the Solar System is bordered by the Oort Cloud which is almost a full LY away from the Sun.)
More Bad News Thus, it follows that we've only traveled a tiny fraction of the distance to our nearest stellar neighbor, Alpha Centauri, about 4 LYs away.
vFin limitation (can't exceed c) - There is a physical limit on spacecraft speed; it can't exceed light speed. This doesn't limit time of acceleration, but it does mean a more accurate model needs us to compute resulting spacecraft velocity in a different way. After a certain point, incremental increases in acceleration time can no longer be modeled by a corresponding linear increase in spacecraft velocity.
Above items are discussed in more detail in Volume 3, Interstellar.
 

Sidebar: Ernest Rutherford

Father of Nuclear Physics

Born 1871 in Nelson, New Zealand, Ernest Rutherford entered Nelson Collegiate School at age 16; in 1889, he was awarded a University scholarship to University of New Zealand, Wellington where he entered Canterbury College. He graduated M.A. in 1893 with a double first in Math and Physical Science; and he continued research work at the College for a short time.
In 1851 (well prior to Lord Rutherford's birth), Prince Albert, husband of Queen Victoria, set up a scholarship fund during the 1851 Crystal Palace Exhibition. Prince Albert specifically wanted to increase opportunities for deserving students outside of England. In 1894, Rutherford was awarded this scholarship; he learned of this while working in his parent's garden and said "this is the last potato that I'll ever dig". Thus, he attended Trinity College, Cambridge as a research student at the Cavendish Laboratory.
His initial experience was not as friendly as he would have liked. As one of the first two nonCambridge graduates to enter their graduate program, he was subjected to some ridicule just for being a provincial. However, his genius quickly asserted itself, and his brilliance could not be denied for very long. For example, he was invited to demonstrate one of his experiments to an evening audience of students, faculty and guests, and Ernest Rutherford did very well. It also helped that he was taken under the wing of the then Cavendish Director, Dr. J. J. Thompson, a brilliant physicist in his own right. (Dr. Thompson discovered the electron.)
In 1898, Dr. Rutherford identified alpha and beta rays in uranium radiation and indicated some of their properties. During this time, he was described by his colleagues as "force of nature". He remained a strong influence on physics throughout his lifetime. Later that same year, he went to Canada to take the Chair of Physics at McGill University, Montreal. There, he discovered new gas, thoron, isotope of radon. With his colleague, Dr. Frederick Soddy, a chemistry professor, he discovered "half-life" of radioactivity.
In 1908, Rutherford was awarded Nobel Prize for Chemistry.
Lord Rutherford died at age 66; his ashes were buried in the nave of Westminster Abbey near the graves of Sir Isaac Newton and Lord Kelvin.

Half Life

Term "half life" means a duration for which a certain substance declines by 50%.
For example, radioactive thorium might decrease by 50% in 60 seconds.
This could be described by
Mtho(1-Δ)t = .5 × Mtho
where Δ is % difference in mass per second and the t is time in seconds.
Divide both sides by Mtho and set t = 60 sec; we get: 
(1-Δ)60 = .5
After some manipulations with logarithms, we get:
60 × Log(1-Δ)=(Log .5)=-0.301
Log(1-Δ)=(Log .5)
60		=-0.005
1-Δ=10-0.005=0.98855
Δ=1 - 0.98855 =0.01145
Now, we determine amount of time for any amount of radioactive decay.
For example, how much time (in seconds) to decay to 10% of original?
(1-Δ)t=.1
t=Log .1
Log(1-.01145)		=200 sec

posted by JimODell at 3:37 AM

0 Comments:

Post a Comment

<< Home