TERRESTRIAL TUG UPGRADES...

TERRESTRIAL TUG UPGRADES....

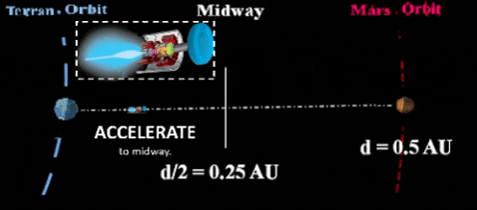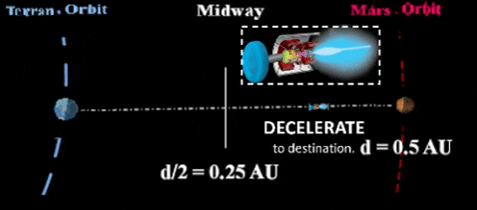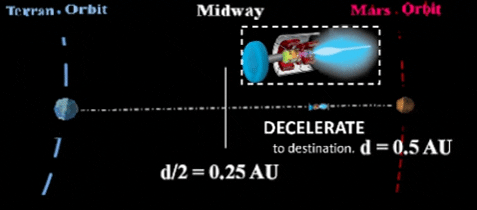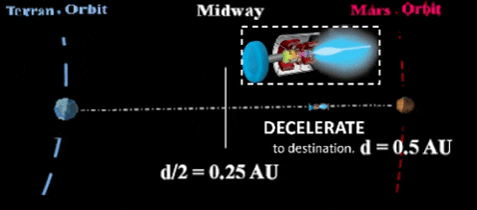
to interplanetary capability.  Initially, space tugs might service the many artificial satellites around Earth as well as transport pax/cargo among many terrestrial habitats and Luna.  Eventually, tugs will expand their service to shifting between many planetary systems and many types of habitats such as orbiters, cyclers and even migrators as discussed in VOLUME I: ASTEROIDAL. Three possible ways to power such interplanetary space tugs include traditional chemical reactions, the now frequently used plasma engines (EXAMPLE: VASIMR as manufactured by Ad Astra Corp, led by Dr. Chiang-Diaz, Scientist, Astronaut & Entrepreneur.) Third, we discuss Thought Experiment's own brainstorm which nationalizes a space borne particle accelerator to someday enable G-force flights throughout the Solar System.
 

CONTENTS
TRADITIONAL CHEMICAL PROPULSION
CONTROLLED PLASMA LEAK
BRAINSTORM G-FORCE
1.	EXHAUST PARTICLE SPEED
2.	SHIP ACCELERATION (AShip)
3.	SHIP MASS (MShip)
4.	RELATIVISTIC GROWTH FACTOR (n)
5.	PROPULSION EFFICIENCY (E)
6.	EFFICIENCY FACTOR (ε)
7.	DAILY DIFFERENCE (∇Day)
8.	TYPICAL FLIGHT DURATION
9.	TOTAL DIFFERENCE (∇Ttl)

 TRADITIONAL PROPULSION USES CHEMICAL REACTIONS

1) Current Technology - Chemical Reactants: Chemical rockets use enormous quantities of fuel to travel from surface to Low Earth Orbit (LEO) and higher.  Once free of Earth gravity, they use short burns to leave Earth's orbit, enter a transfer orbit from Earth's orbit to Mars's orbit; then, accomplish a second short burn to enter orbit around Mars. With only chemical reactants, the shortest possible trip to Mars would be 6 months in a partial orbit. Most trips call for a much longer duration. Most practical use for chemical reactants would be to move vehicle from Earth's surface to Low Earth Orbit (LEO).  HOWEVER, this risky maneuver should be avoided if space elevator functionality is ever accomplished.   REVIEW: Traditional chemical rockets have high impulse, but they're slow and consume lots of fuel.  Thus, chemical propulsion uses short duration "burns" to enter/exit TRANSFER ORBITS. Such orbits are largely constrained by Kepler's laws of orbital motion around the Sun.  Current design limitations constrain a chemical fueled rocket to short period "burns".	Chemical rockets combine chemical reactants (such as hydrogen and oxygen) for a quick "burn",
CONTROLLED PLASMA LEAK ACCELERATES VESSEL
2) Pending Technology - Plasma Drive:Use carefully controlled plasma leaks for constant (though small) thrust throughout the trip. This propulsion provides a constant acceleration to midway; then, deceleration from midway to destination.  The resulting trip could be as short as 3 months. Plasma Performance is Better. Reason for plasma's improved performance, plasma engine constantly propels spacecraft (via plasma ion exhaust) throughout the voyage; this achieves greater speed and does not constrain the vessel to a purely orbital path. Plasma engines heat gases to plasma state (millions of degrees). Thus, rocket performance improves with hotter exhaust; thrust greatly exceeds that of chemical reactants which only reach thousands of degrees in a conventional rocket engine. Thrust from the plasma engine could boost a spacecraft for a longer time and with better efficiency than conventional engines. Plasma engines would have much longer thrust than conventional rocket engines. (Specific impulse.)	Typical plasma engine stays on throughout the entire trip to constantly increase velocity. In fact, vessel speeds so much that flight profile calls for a "slow down" at mid-way. At exactly mid-way, vessel flips around to propel in opposite direction and start decelerating. Otherwise, the vessel would arrive at destination way too fast for orbital insertion.

BRAINSTORM G-FORCE
3) Particle Accelerator Propulsion (TE'S Brainstorm) While shorter than 6 months, 3 months is a long time to spend in near 0-g conditions. A more practical use for a plasma engine might be as a plasma injector into a synchrotronic propulsion system. Thought Experiment (TE) suggests a third choice. Present day accelerators routinely take ions to near light speeds; thus, TE conservatively assumes exhaust particle velocity of .866c (approaching light speed) which introduces a relativistic growth factor (n) of 2 (particle goes so fast, mass doubles). Considering both this enormous velocity and relativistic growth of exhaust particles, TE uses simple momentum exchange equation to show that particle exhaust flow of .1 gm/sec will propel a 5 mT vehicle about 10 m/sec faster for every second of powered flight. Such acceleration provides g-force to simulate Earth surface gravity (g-force) during powered portions of flight. Furthermore, a trip time to Mars reduces from months to just days, a much more reasonable duration.	For a third propulsion option, Thot Experiment brainstorms a notional process where a hollowed out asteroid with a synchrotron continually pumps out grams/sec of ions at 86.6% c. Such momentum could propel many tons of spacecraft at g-force.
For following nine factors, TE compares all three propulsion methods.
1. EXHAUST PARTICLE SPEED (VExh)
Exhaust particles at .866c can propel a large vehicle at g-force (9.806 m/s2).
Exhaust speed of particles expressed as decimal light speed VExh = dc × c Compute dc, decimal component of light speed:   dc = VExh / c If vExh is already expressed as decimal c;  then, determine dc by inspection. EXAMPLE: If VExh = .866c; then,  dc = .866.	TYPE DRIVE VExh REMARKS Chemical Reactants 0.0c If no "burn" during entire trip, then exhaust particles are static inside the vehicle. Plasma  Drive .0033c TE generously assumes controlled plasma leaks about 1 million m/sec, about 1/3 of 1% light speed (c). Particle Accelerator .866c TE conservatively estimates accelerated protons exit from particle accelerator at 86.6% c; much less then routinely achieved with current technology.
2. SHIP ACCELERATION (AShip)
TYPE DRIVE AShip REMARKS Chemical Reactants 0 g With no propulsive force, ship is constrained to orbital velocity. Thus, TE assumes zero acceleration. Plasma Drive .0005g  AShip = 19.2845 km/sec  45 days 1) Reduces to average velocity gain  of about 0.005 m/sec.  2) Divide by g (9.8m/sec²) to convert to "decimal g".  3) Result: Less than 0.1% Earth gravity, very little g-force! Particle Accelerator 1.0 g g is 9.80665 m/sec², acceleration of a free falling object near Earth's surface. TE assumes g as the value for ship's acceleration.  EQUIVALENCE:  Crew feels same downward force (g-force) as Earth surface gravity. NOTE: AShip= Acceleration of vessel in decimal g.	EXAMPLE: Typical plasma drive for typical Mars profile. AShip = ΔV Δt = (V1 - V0) (t1 - t0) Let velocity: V0 = 0; let time: t0 = 0. Let V1 = VMax; let t1 = tMid. Step 1: Determine acceleration in meters per second per second (m/sec2). AShip = VMax  tMid = 19.2845 km/sec 45 days AShip = 19,284.5 m/sec 3,888,000 sec = .00496 meter sec² Step 2: Convert to decimal g (dg) as shown. dg = AShip g = .00496 m/s² 9.8065 m/s² = .0005 g

3. SHIP MASS (MShip)
G-force Examples ffSec Plasma Drive MShip Particle Accel MShip 1 g 201.77 mT 26.47 mT 2 g 403.52 mT 52.94 mT 3 g 605.29 mT 79.42 mT Given dc dg ×  c g × ffSec dc ×  c g × ffSec dc= .0033; dg= .0005 Let dc= .866; dg= 1 NOTE: Ignore relativistic growth in this example. Later, we point out rate of fuel consumption (ffSec) differs from the rate of fuel particle exhaust (ffExh). c = 299,792,458 m/s g = 9.8065 m/s per second Thus, for each second, constant: c/g = 30.57×106 CONCLUSION For one gram/sec (ffSec) of consumed plasma ions,  plasma drive might potentially push a heavier load at a much slower acceleration than Part. Accel. HOWEVER, total travel time is much longer duration.  (For Mars, plasma drive trip might take 90 days  vs. 2 days for Particle Accelerator.) TE assumes typical plasma drive vessel could not maintain this fuel consumption rate for so long.	If ffsec  is in grams (g), MShip  is in metric Tonnes (mT). MShip = (dc×c) × (ffExh)  / (dg×g) TYPE DRIVE MShip REMARKS Chemical Reactants n/a With no propulsive force, ship's mass is unconstrained. Plasma Drive 201.7 ×106ffSec Given particle exhaust speed at 1,000,000 m/sec, and ship acceleration about .0005g, ship's mass is constrained at about 200 million times the mass of exhaust fuel expelled per any given second. MShip = dc dg × c g ×ffSec = 2.017×106 ffSec Particle Accelerator 26.47 ×106ffSec Ship's weight is constrained to about 26 million times the mass of exhaust fuel expelled per second.(disregard relativity)
Two kgs/sec of exhaust particles at .866c can g-force propel a vehicle of 52 kiloTonnes. However, g-force fuel consumption must factor in Relativity and Efficiency.

4. RELATIVISTIC GROWTH FACTOR (n)
TYPE DRIVE n REMARKS Chemical Reactants 1 Since static particles have zero velocity, relativity does not bear. Plasma  Drive 1.001 Since one million m/sec is slow relative to c, relativistic mass growth is very slight. Here, it is optimistically estimated as a thousandth. Particle Accelerator 2.000 At .866c, Lorentz Transform tells us that particle's relativistic mass is double the particle's mass at relative rest. Relativistic growth factor (n) comes from the Lorentz Transform which can be used to quantify mass growth due to relativity. ffSec: fuel flow per second, mass per second consumed at rest.  This quantity converts to plasma prior to injection into particle accelerator. Note: n can be any rational number >1.0, but choosing certain dc values gives integer growth factors.   Choosing particle exhaust speeds with corresponding growth factors as integers is a convenience but in no way a requirement.	n = 1 √(1-dc2) dc= √(n2-1) n √(n2-1) From LORENTZ  TRANSFORM (LT) Solve LT for dc Product of dc× n.       n dc 1 0.0 c 2 .866 c 3 .943 c Given √(n2-1) n ffExh: exhaust mass / sec exits the spacecraft for propulsion. Due to relativistic speeds via particle accelerator, consumed fuel mass grows to become fuel flow exhaust. ffExh =  ffSec √(1-dc2)  =  n × ffSec

5. PROPULSION EFFICIENCY
Efficiency (E) is a value between 0 and 100%, which quantifies how much input is deflected from output performance.  This decrease reflects inevitable design flaws and peripheral needs.  Theoretically, a perfect design would yield: E= Input/Output = 100% Alas, perfect efficiency will always elude us; however, continuing design improvements will always  take us ever closer.  Thus, propulsion efficiency will likely start out low as we journey to nearby destinations (like Mars and Ceres). However, TE assumes E will gradually increase as we design better vessels to journey to further destinations.	Relativity: as initial fuel mass speeds up from relative rest (0 m/s) to .866c, initial 1.0 kgm per sec grows to an exhaust flow of 2.0 kgm per second. Theoretically, this should g-force propel a vehicle of 53,000 mTs. MShip = (dc×c) × (n×ffsec)  / g MShip = dc × 30.57×106× (n×ffsec)  MShip = .866 × 30.57×106× (2×1.0 kg) = 52,947 mT  However, above equations disregards inevitable inefficiencies.  Like all other systems, G-force spaceships will never achieve 100% efficiency; however, the conversion rate from at rest, consumed particles (ffsec) to near light speed, exhaust particles (ffExh) will improve over time.
TE previously disregarded efficiency concerns to determine a g-force ship of 52,666 mTs theoretically requires consumption rate of 1.0 kg/sec (ffSec).  This consumed quantity of particles must accelerate to .866c (VExh) to relativistically grow to 2.0 kg of exhaust particles (ffExh). Since inefficiency is inevitable, optimistically assume E=70%. thus, we assume 70% of the 2.0 kg survives the particle acceleration process.  Sadly, this results in 70% of the desire thrust with only 70% g-force.  G-force vessel must compensate for this shortfall by increasing the consumption rate.	Since system inefficiencies are inevitable, actual thrust produced from theoretical fuel consumption requirement will be much less then needed for g-force. For this example, TE optimistically assumes system efficiency of 70%.  Thus, system inefficiencies divert 30% of plasma particles away from the thrust stream. Relativity increases the consumed 1 kg of fuel to 2 kg; HOWEVER, only 1.43 kg would actually exit the vehicle in the exhaust flow. In this arbitrary scenario, an on-board weight scale would measure a 100 lb object at only 70 lbs. CONCLUSION: At 70% efficiency, fuel consumption of 1.0 kg produces enough thrust for only .7g-force. Thus, TE uses an efficiency factor (ε) to determine added consumption required for g-force.
6. EFFICIENCY FACTOR (ε)
Efficiency Factor (ε)  is reciprocal of Efficiency (E). ε = 1/E To compensate for inevitable inefficiencies, consumption rate must increase. Therefore, determine the Efficiency Factor (ε) by dividing 1 by E.  Then, determine increased consumption rate by multiplying original rate by ε. EXAMPLE:  if E is 70%, increase consumption from 1.0 kg/sec to 1.43 kg/sec as shown in diagram. TE now uses arbitrary examples of E = 70% and ε = 1.43 as a starting point. Actual g-force flights will provide empirical data tp determine actual Efficiency (E) and Efficiency Factor (ε). Items contributing to inefficiencies might include: Design flaws, for example, particle collisions will likely stop a significant portion of particles from exiting vessel.  Arbitrarily assume this causes 10% inefficiency. Systemic power needs; propulsion system components will need power. particle accelerator devices such as collision detectors, possible even the magnets (see next chapter for more on magnets) will need power even though these components don't directly contribute to propulsion. Arbitrarily assume this causes 10% inefficiency. Auxiliary Power. Life support, comm gear, nav gear and many other items are needed for ship operation and crew comfort, but not part of propulsion system. However, a portion of propulsion power will likely be diverted for these purposes. Arbitrarily assume this causes 10% inefficiency. E  = 100% - 10% -10% -10% = 70%	Actual efficiency data can't be obtained until g-force operations actually begins. Thus, TE must make do with assumptions.  For above three items, TE assumes each requires 10% of propulsion power output: thus, TE arbitrarily assumes an efficiency of 70% (a very optimistic assumption.)  Actual efficiency (E) will need to be validated with empirical data.  ffSec =  ε × MShip  / (dc × 30.57×106 × n)  ffSec  = 1.43 × 52,947 mT / (.866 × 30.57×106× 2 × 1.0)  ffSec  = 1.43 kg  TYPE DRIVE E REMARKS Chemical Reactants 100% Perfect efficiency because no fuel expended, a tautology. Plasma  Drive 100% Very little fuel expended per day; so, this efficiency is close to one. Particle Accelerator 70% Considerable fuel consumption; thus, inefficiencies are inevitable.  If exact values are not yet known, make reasonable assumptions. For g-force propulsion, a 53 megaton vessel must emit an exhaust flow (ffExh) of 2 kg/sec with particle velocity of .866c. To achieve this exhaust flow, theoretical "at rest" fuel consumption rate is 1.00 kg/sec; and relativity will grow the particles to 2.0 kg/sec.  HOWEVER, practical fuel consumption must consider inevitable inefficiencies. Thus, apply the Efficiency Factor (ε), the reciprocal of Efficiency (E).   EXAMPLE:  For E=70%, ε = 1/E = 1.43.  Increasing 1 kg by a factor of 1.43 results in 1.43 kg/sec consumed at rest.  Accelerate this to .866c, and it relativistically grows to 2.86 kg. Since this example assumes 70% survival rate, the exhaust particle flow reduces to 2.0 kg, the amount needed to create g-force.
7. DAILY DIFFERENCE (∇Day)
Ship's mass decreases due to powered flight's fuel consumption.  TE uses term, ∇Day , to describe daily decrease of ship's mass due to fuel consumption.  Recall that g-force ship capacity depends on actual quantity of high speed fuel particles (ffExh) actually expelled. Furthermore, g-force thrust particles are at relativistic velocities near light speed, dc c. Consider following factors: (1) Relativistic growth factor, n, depends on exhaust velocity (VExh). VExh = dc c  Compute n from Lorentz Transform (LT). n = 1 √(1-dc2) (2) Theoretical Exhaust Flow, ffExh ffExh= n×fSec As consumed fuel flow (ffSec) accelerates, mass grows by relativity growth factor, n. ffSec = ffExh n ε  = 1 E (3) Practical fuel consumption, ∇Sec. Fuel flow, ffsec, is consumed at relative rest.  ∇Sec  = ε×ffSec However, this fuel consumption must also account for inevitable inefficiencies. (Efficiency factor, ε, is reciprocal of Efficiency, E). ffDay = 86,400×∇sec (4) Daily fuel consumption can be approximated. Multiply by 86,400, seconds per day. (5) Recall previous work: c/g = 30.57×106 dc× n = √(n2 - 1) For a g-force spaceship, dg = 1. For other drive types, dg << 1. MShip = vExh×ffExh AShip = dcc×nffsec dgg = 30.57×√(n2-1)×106×ffsec dg	TYPE DRIVE ∇Day REMARKS Chemical Reactants 0 No fuel expended. However, no g-force during the flight, and no hurry to get there. Tolerable for robots but not humans. Plasma Drive 0.014% dg=.0005 ε=1 n=1.001 For current plasma propulsion, compute and apply very small values of dg. Particle Accelerator 0.233% dg=1 ε=1.43 n=2 Relativistic growth of n=2 due to exhaust velocity of .866 c, light speed. Resulting momentum enables g-force; thus, dg=1. Arbitrarily assume E = 70%  for  efficiency factor of ε = 1/E = 1/.7 = 1.43. Most daily fuel consumption,  requires .233% of vessel's GW. G-force benefits:  1) inflight comfort 2) quick flight time. (6) ∇Day is a percentage of ship's current gross weight (%GW). Daily decrease of ship's GW (∇Day ) depends on Efficiency Factor (ε), relativistic growth (n) and ship's acceleration (dg, expressed as decimal).  ∇Day = ffDay MShip ∇Day = ε× 86,400 × ffsec 30.57×√(n2-1)×106×ffsec/dg ∇Day = ε × dg × 86,400 30.57 × 106 × √(n2-1) ∇Day = ε × dg × 0.283% GW √(n² - 1)

8. TYPICAL FLIGHT DURATION (t)
Type Drive Travel TIme REMARKS Chemical Reactants 180 days Flight profile calls for a partial orbit at orbital speeds. Plasma  Drive 90 days A small amount of constant propulsion can reduce trip time by as much as half. Particle Accelerator 2 days A constant amount of near light speed propulsion particles can reduce trip time to much shorter durations in much more tolerable conditions
9. TOTAL DIFFERENCE (∇Ttl)
To determine trip's total fuel consumption, accummulate all the daily GW differences for entire trip. NOTE: ∇Ttl = GWFinal - GWInitial= Σ∇Day  Quick way to approximate: Multiply daily diff (∇Day) times total trip time (t). ∇Ttl = ∇Day × t This works well for extremely small daily fuel consumptions or for short trip durations. Both these circumstances exist in following table. TYPE DRIVE FUEL REMARKS. Chemical Reactants 0 No fuel expended during flight. Disregard chemical reactions ("burns") to enter/exit orbit of flight. Plasma  Drive 1.26% For extremely small daily fuel consumptions,  product of trip time times daily fuel consumption: t × ∇Day = 90 dy × .014%GW/day  t × ∇Day  ≈ 1.26% GW0 Particle Accelerator 0.466% For a short 2 day trip, approximate as follows: t × ∇Day = 2 dy ×.233% GW/day  t × ∇Day ≈ 0.466% GW0	EXPONENTIALS However, many flight profiles have significant fuel consumption and/or lengthy trip duration.  EXAMPLE: Let daily fuel consumption to be 1% ship's gross weight (GW). ∇Day = 1% GW/day = .01 GW/day EXAMPLE:  Let total trip duration (t) be 40 days. To determine total fuel consumption, our intuition might mislead us.  Initially, we might estimate total fuel consumption at forty times one percent, for a fuel burn of 40% initial gross weight (GW0).  Thus, if GW0 = 100 mTs; then, total fuel consumptions might be 40 mTs, and final gross weight (GW40) might be 60 mTs.  However, this intuitive approximation would be very imprecise. ∇Ttl = .01 GW/day × 40 days ≈  .4 GW0 GWFin =  GW40 ≈ GW0 - ∇Ttl = .6 GW0 Multiplying daily differences is easy but inaccurate!!! A more accurate model of fuel consumption  might involve exponents. Axiomatic: If daily fuel consumption is 1% gross weight (∇t = .01 GWt), then tomorrow's gross weight will be 99% of today's; GW1 =  .99 GW0 Example: If ship's initial gross weight GW0 is 100 metric Tonnes (mTs), then ship's GW can be computed for first, second and following days: Day 1: GW1 = .99 GW0 = 99 mT Day 2: GW2 = .99 GW1= .99 × 99 mT =  98.01 mT Day t: GWt = .99 GWt-1= (1 - ∇Day)t × GW0 Day 40: GW40 = .9940  × 100 mT =  66.897 mT Exponentials more accurately determine fuel consumption  for longer duration flights.

SUMMARY:  In coming days of powered flight, ship's Gross Weight (GW) decreases due to fuel consumption.  Subsequently, slightly lighter ship requires slightly less fuel; thus, absolute fuel consumption decreases even though percentage Gross Weight (%GW) remains the same.  To model this, TE initially considers a convenient rate of fuel consumption (ffsec=1.0 kg/sec); then, TE determines ship's GW. For particle exhaust speed (VExh) of 86.6% light speed (c),  relativity doubles mass size; thus, growth factor(n)=2. Thus, √(n2-1) = 1.73.  For g-force propulsion,  dg = 1.  MShip = 30.57×√(n2-1)×106×ffsec dg For convenience, consider fuel flow (ffsec) of 1.0 kgm/sec.  Theoretically g-force propels a ship of 52,886 mTs. However, it's much more likely that flight planners will first determine Take Off Gross Weight (TOGW); then, flight engineers will determine practical fuel flow requirements based on planned TOGW and known efficiency factor (ε).

Sidebar: SPECIFIC IMPULSE(Isp) Type Drive VExh Isp Solid rocket 2,500 m/sec 250 sec Bipropellant liquid rocket 4,400 m/sec 450 sec Ion thruster 29,000 m/sec 3,000 sec VASIMR 30,000-120,000 m/sec 3,000-12,000 s Part. Accel. Propulsion .866c≈260,000,000 m/s 26,000,000 sec GIVEN OBSERVED VExh /g Specific impulse is measured in seconds. EXAMPLE: one pound of typical solid rocket motor fuel produces one pound of thrust for 250 seconds. Specific Impulse (Isp) is the length of time (usually “seconds”) that each unit weight of propellant propels its own weight.  For ships in vacuum of space, it proves convenient to compute specific impulse as average particle exhaust speed divided by g, near Earth gravity.

SLIDESHOW

---

---

---

VOLUME O: ELEVATIONAL VOLUME I: ASTEROIDAL VOLUME II: INTERPLANETARY VOLUME III: INTERSTELLAR

---

---

---