MOMENTUM MAKES IT HAPPEN
Action Causes Reaction.
|
Let a small mass of high velocity, exhaust particles exit a rocket in aft direction;  subsequent momentum increases forward speed. |

MOMENTUM is mass times velocity, m × v.
Momentum is a conserved quantity.
Within a closed system of interacting objects, total momentum of entire system remains constant. When object A collides with object B in an isolated system, total momentum of the two objects before the collision is the same as the total momentum after the collision. Any momentum lost by object A goes to object B. | P = M × V = m × v = p Product of large mass × slow velocity
will equal product of small mass × fast velocity. Express momentum relationship between fast moving fuel particles and a slow moving spaceship:
Mship × Vship = mfuel × vfuel
Thought Experiment (TE) assumes following items:
1) For every second of powered flight, space vessel's speed increases by 10 meters per second (m/s). Thus, Vship is a constant 10 m/s. This value closely approximates g, acceleration due to gravity near Earth’s surface. Thus, TE assumes our notional spaceship can expel enough high speed particles to provide gravity equivalence throughout the flight. This simulates Earth gravity for ship and contents.
2) Let the fuel consumption be one gram of particles for every second of powered space flight. I.e., set mfuel to a constant 1.0 gram. 3) Assume spaceship's propulsion uses an onboard particle accelerator to give exhaust fuel particles extremely high speeds. Since current devices easily accelerate particles to 99% of light speed, our thought experiment will eventually sustain fuel exhaust velocity, vfuel, to near light speed, c. 4) Rename the vfuel term as "vExh" to more clearly indicate exhaust velocity of particles exiting vessel. We choose to independently vary vExh by incrementally increasing from row to row in the following tables. Thus, vExh is our Independent Variable (IV). | ||||||||||||||||||||||||||
TABLE-1: CONSISTENT UNITS For consistency, TABLE-1 uses grams and meters per second (m/s) on both sides of momentum exchange equation.
MShip × VShip = mfuel × vExh
Solve for Mship to determine how much ship's mass can be propelled 10 m/s by a given mass of high speed fuel particles in opposite direction. Since Mship depends on the value of vExh, Mship is our Dependent Variable (DV).
EXAMPLE
|
Momentum Exchange.
Thus, total momentum of a system of objects is "conserved"; total amount of mass times velocity is static. To further understand momentum conservation, consider Newton's Law of Momentum Conservation. When two objects collide, the forces acting between the two objects are equal in magnitude and opposite in direction. In equation form,
m × v = -M × V
The forces between the two objects are equal in magnitude and opposite in direction, which leads to Newton's Law of Momentum Conservation. In a collision, the momentum change of object A is equal and opposite to the momentum change of object B. That is, the momentum lost by object A is equal to the momentum gained by object B. In a collision between two objects, one object slows down and loses momentum while the other object speeds up and gains momentum. If object A loses 75 units of momentum, then object B gains 75 units of momentum. Yet, the total momentum of the two objects (object A plus object B) is the same before the collision as it is after the collision; the total momentum of the system (the collection of two objects) is conserved.
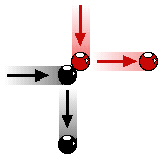 For any collision occurring in an isolated system, momentum is conserved - the total amount of momentum of the collection of objects in the system is the same before the collision as after the collision. For any collision occurring in an isolated system, momentum is conserved - the total amount of momentum of the collection of objects in the system is the same before the collision as after the collision.
This exchange can be readily observed by watching billiard balls collide.
|
Table-1 calculations are straight forward;
however, two terms, vExh and MShip, have a lot of inconvenient digits. simplify this process by mixing some units.
Express vExh as dc × c
"decimal c" times light speed
For convenience, mix different velocity units. In particular, we'd like to continue expressing ship's velocity increase, VShip, as 10 meters per second (m/s); but we'd like to change vExh units from meters per second to decimal light speed, dc × c, c remains the light speed constant, c = 299,792,458 m/sec; dc is the variable decimal component.
Decimal Component (dc) is the ratio of vExh to c:
dc = vExh / c
EXAMPLE: Let vExh = 60 million meter/second;
then, dc = 6×107 m/s ÷ 30×107 m/s = .2
Express Mship as metric Tonnes (mT)
For added convenience, mix different mass units. Continue using "grams" for fuel mass burned every second of powered flight; HOWEVER, now express ship's mass in metric Tonnes (mTs). By definition: 1 mT = 1,000,000 gms; thus, TABLE-1's example value of MShip=3,000,000 gms changes to 3 mT for TABLE-2. (For reference, a large pickup truck is about 3 metric tons.)
|
TABLE-2: MIXED UNITS
For convenience, change from consistent units (grams and m/s) to mixed terms. Thus, express Mship in mT and vExh in decimal c.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
TABLE-3: USEFUL RATES
Rearrange for following:
Express Term, c/g, as a constant.
NOTE: Precise values.
Following table shows that both fuel flow quantity
and fuel particle exhaust velocity can be independent variables.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
With Newtonian mechanics, we propose that expelling one gram of high speed particles (ffsec) at a velocity of .1 c (vExh) is sufficient to propel a 3 metric Tonne (mT) ship (Mship) at 1-g-force for one second.
We now propose that at near light speeds; relativistic effects further increase the propulsion. To quantity this mass increase due to near light speeds, we use the Lorentz Transform.
Lorentz was awarded the Nobel Prize in 1902, but his subsequent "Lorentz Transformation" (LT, published 1904) was based on electromagnetic forces between charges slightly changing due to their motion, causing moving bodies to slightly contract. Among other things, LT paved the way for Einstein's special theory of relativity, which was published 1905, the year after Lorentz published his famous transform. (Einstein’s Nobel Prize awarded 1921). Of course, relativistic effects are due to nature of matter discovered by Einstein’s famous e=mc2 equation. These relativistic effects can be quantified and measured by using the equation associated with the Lorentz Transform (LT). 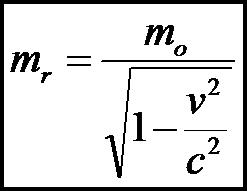 For example, if a small original mass (mo) could accelerate in a particle accelerator to a significant portion of c, speed of light; its size would grow to relativistic mass (mr) as shown by equation at left, Lorentz Transform. For very small values of v (say speed of bullets, 1 km/s, or even slower speed of automobile, 100 km/hr = .028 km/s), v is so much less then c, 300,000 kilometers per sec, that LT's radical expression is extremely close to one (1.0) with virtually no mass increase. Thus, for everyday speeds, moving mass equals original mass. |
LEVERAGE LORENTZ TRANSFORM
| |||||||||||||||||||||||||||||||||||||||||||
For simplicity, TE artificially assumes every particle introduced into particle accelerator as ffsec will successfully travel through many kilometers of pathways and exit the exhaust to propel the spacecraft. Thus, relativistic effects will increase original fuel flow per second ffsec to exhaust fuel flow, ffExh:
| 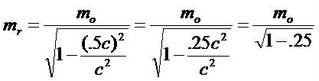 To quickly realize significance of Lorentz Transform (LT), arbitrarily pick a speed much higher then what we observe everyday; for example, one half the speed of light or .5 c for following equations. To quickly realize significance of Lorentz Transform (LT), arbitrarily pick a speed much higher then what we observe everyday; for example, one half the speed of light or .5 c for following equations. After particle accelerates to .5c, the mass increases an observable 15%. TABLE-5 shows even greater increases for even higher speeds. | |||||||||||||||||||||||||||||||||||||||||||
| TABLE-4: SHIP SIZE CAPABILITY
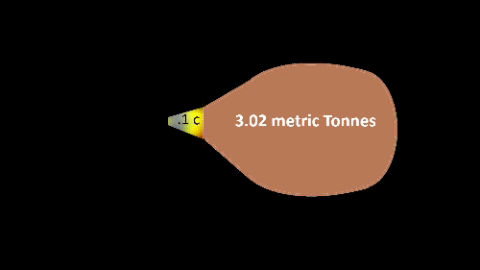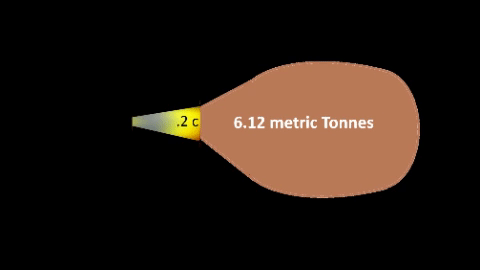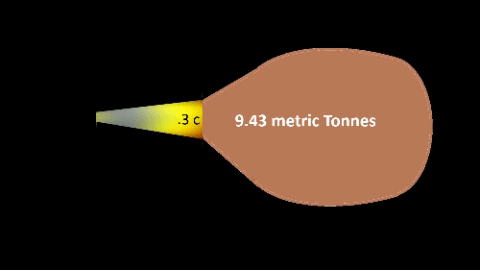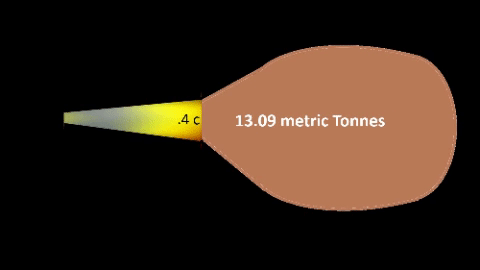 Fuel flow (ffSec) is consumed at non-relativistic rate; Fuel flow (ffSec) is consumed at non-relativistic rate;
TABLE-4 maintains ffSec at constant 1 gm/sec.
Fuel particle exhaust (ffExh) is expelled at relativistic rate
to increase both momentum and propulsion capability.
|
|
In brief, accelerating particles to near light speed increases their mass:
Thus far, we've taken the Momentum Conservation equation and applied it for a duration of one second.
For space travel to become routine, technology will have to accomplish two things:
|
SUMMARY

Both micro-scale and macro-scale fuel consumption are now in current modes of transportation, (for example, the typical plane, train, and automobile have done this for many years). However, can micro/macro scale energy conversion be done for exhaust particles accelerated to large portions of c, speed of light???
Note: for current state of aerospace nuclear propulsion,
edited by Claudio Bruno.



0 Comments:
Post a Comment
<< Home