BEAM ME OUT!!!
Go Outward, Beyond GEO.
Physical tether's "Out-Link" segment between Geosynchronous Equatorial Orbit (GEO) Node and Apex Anchor (AA) can theoretically launch payloads to greater Earth orbits and interplanetary destinations. However, Thought Experiment (TE) proposes a virtual "Out-Link" tether with GEO parked vehicles using "ion drives" either internally hosted or supplied by external "space tugs" which push vehicles as required. For launching payloads outward, such a solution might prove much more practical than an 100,000 km Carbon Nano-Tube (CNT) tether destined to break at some point along its extended length.
| BACKGROUND: PHYSICAL TETHER. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
Out-Link tether enables delivery of payloads beyond GEO. Stretching from GEO Node to Apex Anchor (AA), an Out-Link tether sits atop the Up-Link, bounded by a GEO Node.
Out-Link provides ever increasing centrifugal force to push climber further out from Earth. Along the Out-Link tether, outermost points have sufficient tangential speeds for payload satellites to escape Earth's orbit and travel "interplanetary" throughout the inner Solar System. Tether has theoretical advantage over the ion beam. THEORETICALLY, tether vehicle can easily increase tangential velocity by climbing ever outward. With constant angular velocity of 15°/hour, linear velocity ever increases as Out-Link Tether radius increases. Well prior to 100,000 km from Earth surface, climber easily gains sufficient speed to launch interplanetary payloads. Of course, there is the enormous drawback; taut tethers will inevitably snap like a rubber band regardless of theoretical strength of CNT strands. Thus, physical tether will most likely remain theoretical and never become practical. WITHOUT TETHER. Perhaps, vehicles can transit GEO without the tall tether. Thus, TE proposes a more practical way to
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| GEO IS INNER CIRCULAR ORBIT. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Orbit Bound Vehicles
must comply with Kepler's Third Law. Thus, orbital velocity slows as orbit elevation increases.  |
Circular orbit maintains a fixed distance around the center; thus, it is shaped like a circle. In addition to constant radius, standard assumption for circular orbit includes constant linear speed and angular speed throughout the orbit as well as constant equivalence between gravity and centripetal force. Two specific examples follow:
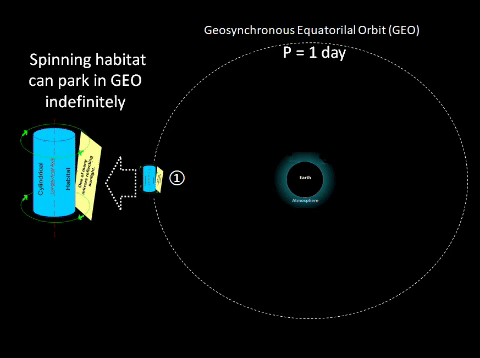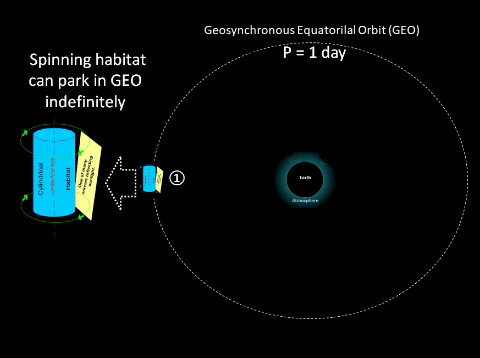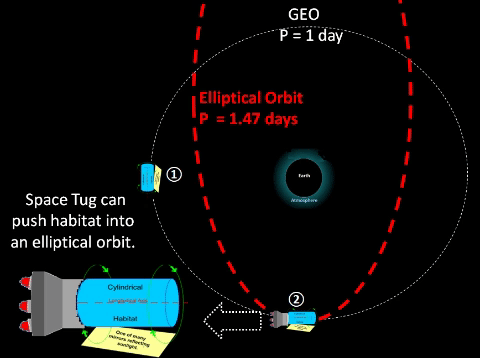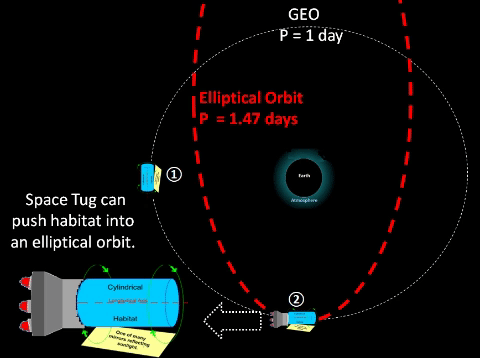
Synchronous Orbit The well known Geosynchronous Equatorial Orbit (GEO) is a circular orbit with constant radius of 42,228 km from Earth's center. At this radius, an object orbits around the Earth at exactly same rate of rotation as the Earth's equator about the Polar axis. Thus, a GEO object synchronizes with constant nadir on Earth's Equator. Resonant Orbit For convenience, Thought Experiment (TE) proposes another equatorial, circular orbit with radius of 67,048 km; such an orbit would have a period of exactly 2 days and would resonate with GEO. Every two days, an object in this orbit would line up exactly with an GEO object and Earth's center (i.e., co linear). GEO has many advantages over other orbits, HOWEVER, an outer circular orbit does offer an advantage; it has a lesser escape velocity. How does one move a GEO object to park in an outer orbit where it will eventually, more easily launch an interplanetary mission?? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| START TRANSFER ORBIT. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Constructed in Geosynchronous Equatorial Orbit (GEO), space borne habitats will provide comfortable quarters for many 1,000's of families. Outer hull will spin around longitudinal axis to simulate Earth gravity; large co-located mirrors will direct sunlight for energy; food and oxygen will come from extensive on board agriculture (trees and crops). Habitats can park indefinitely in GEO or they can transition via "transfer" orbit to an outer orbit. EXAMPLE: Thought Experiment (TE) proposes a "space tug" to gently push habitat into an elliptical orbit with semi-major axis (a) of 54,638 km and Earth as the focus. |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| COMPLETE TRANSFER ORBIT. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ENTER OUTER CIRCULAR ORBIT. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
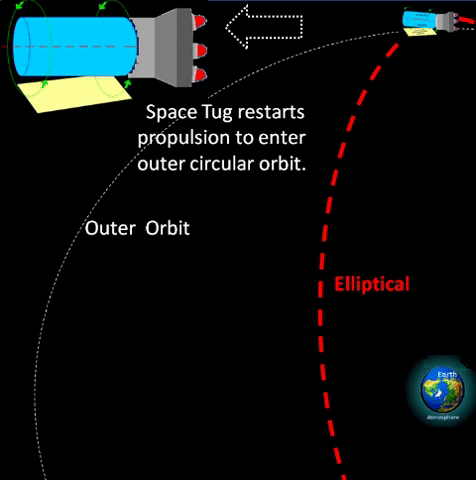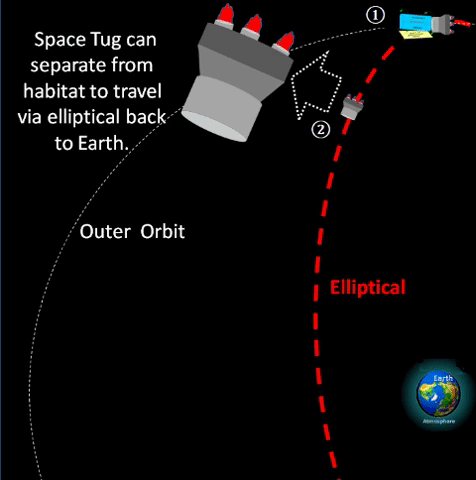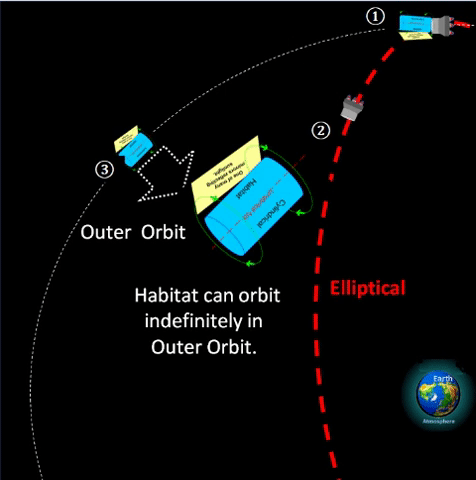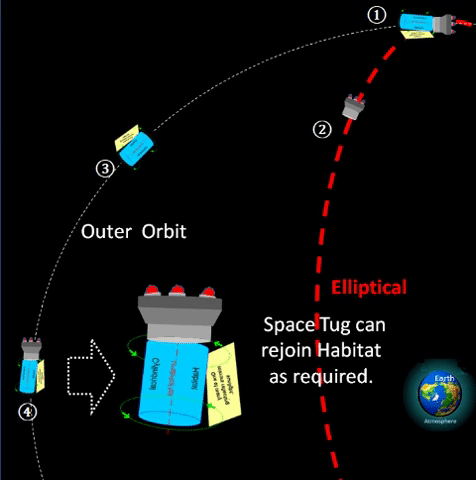| SUMMARY: USE ELLIPTICAL TO TRANSFER FROM GEO TO OUTER. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
❶ Vehicle can park indefinitely at GEO.
❷ With space tug assist, vehicle can exit GEO to enter elliptical. ❸ During the semi-orbit from q to Q, vehicle can apply additional burn to maintain course or to go to another destination circular orbit. ❹ At Q, elliptical apogee, vehicle can again apply more burn to enter expanded circular orbit. ❺ Space tug can return to original GEO platform via elliptical orbit. ❻ Vehicle can park indefinitely at expanded circular orbit, or it can eventually apply more burn to escape Earth's gravity and go interplanetary.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lunar Phases
are shown below. Different views of the moon depend on relative orientations of Sol, Luna and Terra 
Thought Experiment (TE) assumes maximum distance (Q) from Terra could happen during Full Moon. TE further assumes minimum distance (q) could happen during New Moon; Q and q define Lunar ellipticity. Mean distance could be the average of Q and q.
For convenience, TE arbitrarily assumes Luna is on circular orbit (see right side diagram) with Lunar orbit's mean radius, 382,931 km, and Period of 27.3 days. This assumption can be further resolved by one of following methods:
a) Schedule entering elliptical orbit (t=0) so that the Lunar intercept (t=5.65 days) happens exactly when Moon is at mean radius. b) If Lunar distance at intercept (t= about 5.65 days) differs from the mean, the vehicle can make required adjustments with in-transit burns. | 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| CONCLUSION: TE proposes ion drive powered "space tug" to help habitats gain greater orbits about the Earth. Perhaps more powerful space tugs can push habitats to interplanetary orbits.
For more, see VOLUME I: ASTEROIDAL.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
❸
posted by JimODell at 2:14 AM
0 Comments:
Post a Comment
<< Home