BACKGROUND: BASIC ELLIPTICALS
 Recall KEPLER's THIRD LAW: The square of an object's orbital period (T²) is proportional to the cube of the semi-major axis (a³ ) of its orbit. Thus, all Solar orbiting objects can relate to each other as follows:
Recall KEPLER's THIRD LAW: The square of an object's orbital period (T²) is proportional to the cube of the semi-major axis (a³ ) of its orbit. Thus, all Solar orbiting objects can relate to each other as follows:
T1² / a1³ = T2² / a2³
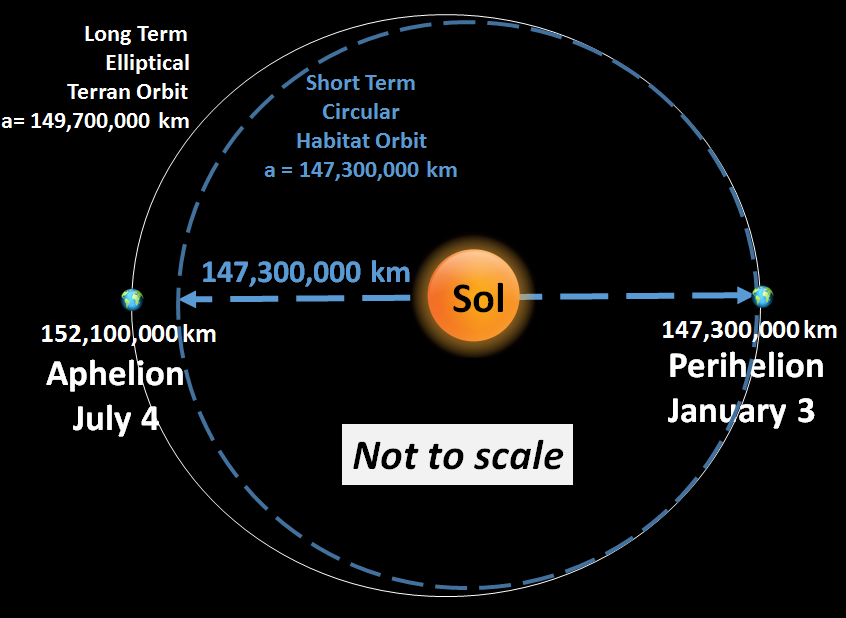
Let T1 = 365.25 days = 1 year
a1 = 149,700,000 km = 1.0 AU (Earth's actual observed elliptical orbit semimajor axis, a)
a2 = 147,300,000 km = 0.98397 AU (a for an artificial circular orbit with Earth's perihelion as radius)
Solve for T2 = √ a2³ = √ 0.98397³ = .976 year = 356.5 days

INITIAL LAUNCH OF HABITAT AND SUPPORT MODULES
REVIEW: Initial Launch of Habitat and Support Modules into Nearby Parallel Orbits.
|
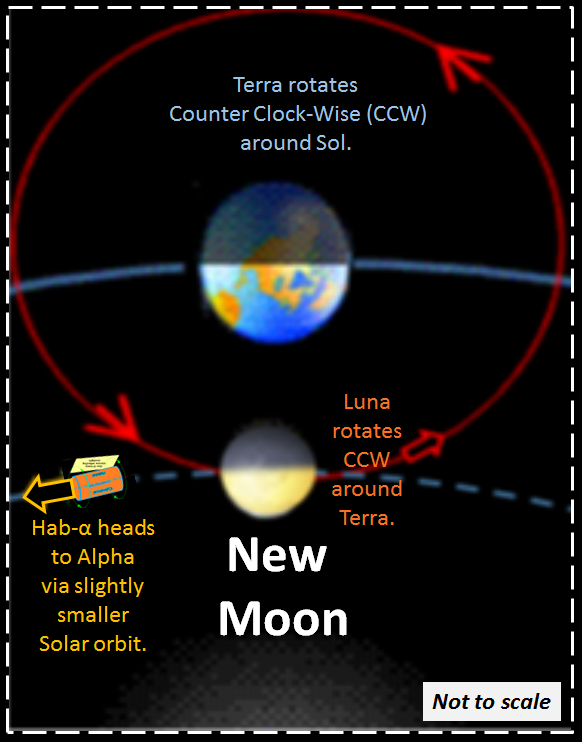 |
Vernal Equinox, March 20, Year 0.
Assume New Moon lunar phase, launch Habitat-Alpha (Hab-α) from Luna, to leverage the slight decrease in Solar Orbit semi major axis (a) gained by New Moon position, 384,000 km decreased orbit about (384/149,700.7) .2565%. Hab-α's slight decrease in orbital a results in slight increase of Hab-α's angular velocity (ω).
Due to the difference in angular velocities, Hab-α slowly increases lead before Terra about .004°/day; this rate would take about 40+ years to reach desired parking spot of 60° before Earth. (Assume Hab-α closely parallels Earth's Elliptical orbit.)
Thought Experiment (TE) assumes that no commercial enterprise will engage on a venture which begins 40 years in the future. TE BRAINSTORMS A GRACEFUL WAY TO REDUCE THIS LENGTHY DURATION.
|
FARTHER CIRCULAR ORBIT
PREVIEW: Subsequent Launch of Completed Habitat into a Farther Circular Orbit.
|
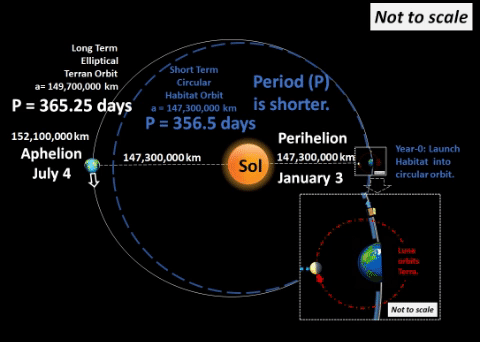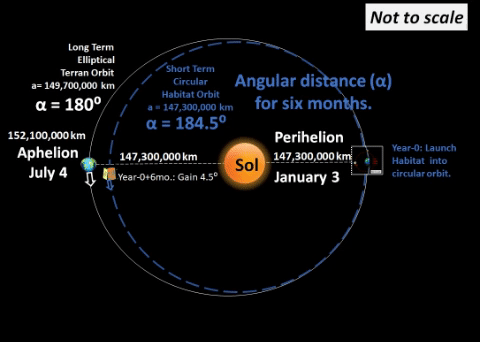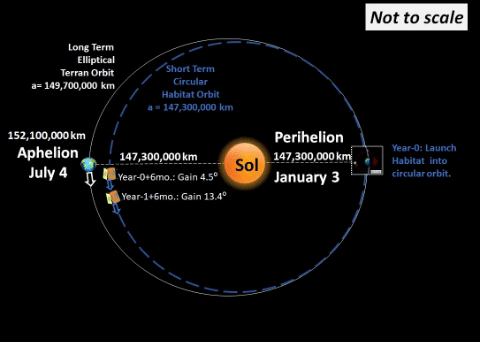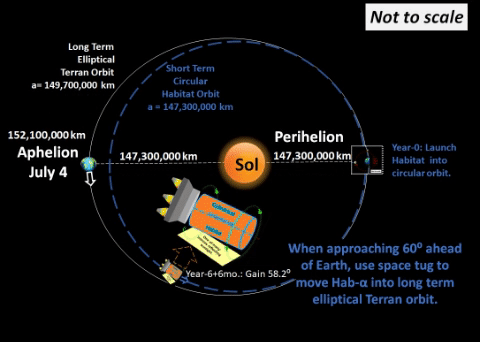
 | Terran Perihelion, January 3, Year 1.
Assume all construction completes before Jan 3;
further assume Hab-α's precise burn
to attain purely circular orbit.
With Earth's perihelion (closest to Sol) as radius,
Period will shrink from 365.25 days
to about 356.5 days.
This significant orbital change,
increases angular velocity of Hab-α.
EXAMPLE: During initial six months,
Earth travels a normal semi-orbit,
but Hab-α travels an additional 4.5°
during this same time, a significant lead. |
| NEXT FEW YEARS, HAB-α INCREASES LEAD. |
In subsequent orbits, Earth consistently passes through the aphelion on same date, July 4. However, Hab-α is on a smaller, quicker orbit, and July 4 continually finds it further ahead.
EXAMPLE: On the second pass, Hab-α increases its lead to 13.4°; on the 3rd pass, lead becomes 22.4°; and so on.
On the 7th pass, Hab-α increases its lead to 58.2°, almost at its final goal of 60° ahead of Terra.
|
 |
 From perihelion (q), Hab-α initiates its own circular orbit and increases its lead from Earth about 9° per year. After about seven years of a smaller, quicker orbit, Hab-alpha reaches it's goal of 60° ahead of Earth. In a similar manner, Hab-Ω enters a larger, slower orbit at aphelion (Q) and increases its lag behind Earth until Year-7. |
| PARKING SPOT |
 |
FINALLY, Hab-α leads Earth by 60°
to attain a persistently parked position.
THUS, habitat exits circle around our Sun
to enter Terra’s actual elliptical orbit.
ASSUME: Sep 18 of 6th year
past original launch.
|
|
ANGULAR VELOCITIES
From Earth's perihelion to aphelion, both Hab-α and Hab-Ω experience a range of angular velocities. |
 |
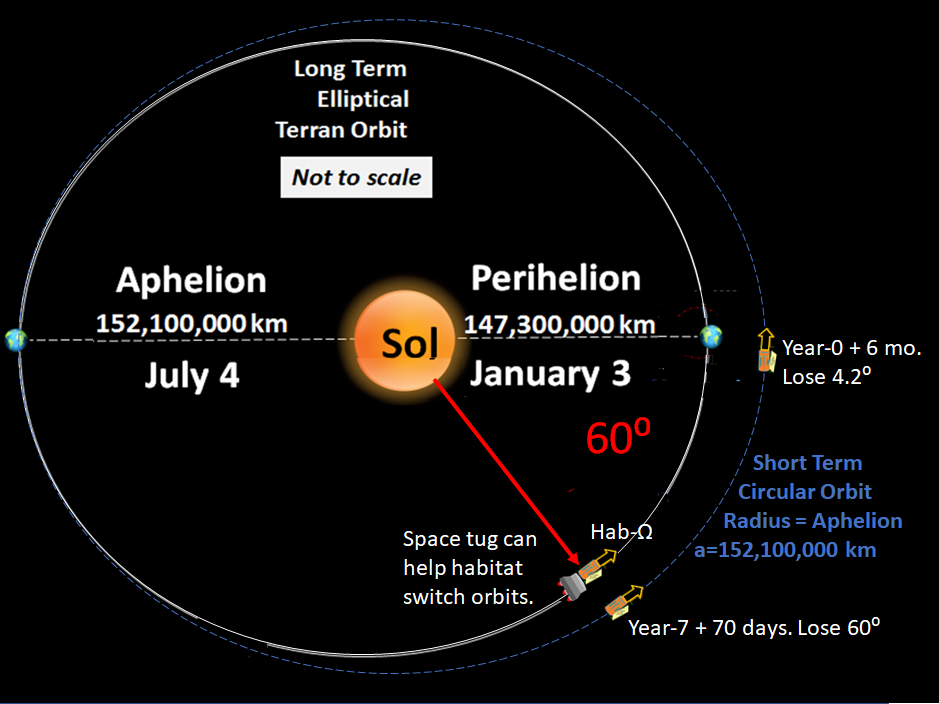
HAB-Ω LAGS EARTH
In above table, at row dated July 4. Earth is at aphelion. Assume a vessel uses a space tug to exit Earth's orbit at this date; then, enter a circular orbit.
In this circular orbit, vessel would orbit slightly slower than Earth's elliptical orbit; and its lag behind Earth would continuously increase. In about 7.2 years, Hab-Ω would reach 60° behind Earth.
To eventually park 60° behind Earth, Hab-Ω needs larger, slower orbit to increase its lag till there.
|  |
SUMMARY
Many experts propose Lagrange points, L-4 (60° before Earth) and L-5 (60° behind Earth) as optimal parking spots for Habitats, which TE calls Habitat-Alpha (Hab-α) and Habitat-Omega (Hab-Ω) respectively. Use following methods to properly place Habitats into Earth's Solar Orbit.
Enter Circular Orbit: On about Jan. 3, Earth arrives at its perihelion (orbit's nearest point to Sol); thus, this is a great position for
Hab-α to enter a circular orbit with shorter semi-major axis and thus reach L-4 in about 6½ years (without this circular orbit, it would take about 40+ years to reach L-4). Alternatively, Earth arrives at aphelion (farthest from Sol) on about July 4; thus, a great position for Hab-Ω to enter a circular orbit with larger semi-major axis to reach L-5 in about 7 years.
Park at L4/L5: Final burn needed by each Habitat when they each reach designated parking spot; perhaps provided by a
space tug.
CONCLUSION: 7 years travel time is much better than 40 years travel discussed in previous chapter attained by Lunar Launches from either Full Moon or New Moon.
TRANSITION: HOWEVER, we can do even better. Properly oriented cycler orbits can reduce travel time to two years or even less, discussed in next chapter, LEVERAGING LAMBDA.




0 Comments:
Post a Comment
<< Home