A Thought Experiment: PUSH PARTICLES TO INTERPLANETARY

Our thought experiment proposes performance envelope for interplanetary travel via accelerator propulsion. This performance must greatly exceed that of current ion thrusters. These transform gas particles to ions and discharges them to propel a craft. As the high speed (perhaps 30 km/sec) gas ions exit the spacecraft, they push the spacecraft in the opposite direction.

Making the leap from ion drives to on board particle accelerators will be an enormous technological challenge. While current ion propulsion greatly reduces travel time to nearby planetary destinations, it has serious limitations. The travel time is still lengthy, i.e., several months to Mars at near zero g conditions. However, Thought Experiment (TE) proposes a sufficient flow of extremely high speed (10% to 50% c, light speed) exhaust particles to accelerate vessel at rate, g (about 10 m/sec²). Such performance will enable Einstein's "equivalence" (simulating gravity), and quick flights to near by planets will become routine.

EXPAND ENVELOPE

from current ion propulsion ... which exhausts milligrams/sec of xenon ions at about 30 km/sec to accelerate a relatively small vessel much slower than g. Thus, flight time to Mars reduces by a few months. Vessel occupants will experience "micro-g" conditions.

to onboard particle accelerator ... which will transform several grams/sec of water to ions and expel them at speeds from 10% to 50%c (about 30 to 150 million meters per second). Thus, flights to nearby planets will be relatively quick (days to weeks). Furthermore, such propulsion can produce equivalence (occupants feel same gravity as if static on Earth's surface); thus, the term "g-force".

Review some assumptions:

I. Assume onboard particle accelerator....

...can consume reasonable quantities of fuel particles, original fuel flow per second (ff_sec), and accelerate them into a constant flow of exhaust particles (ff_Exh) .

For this initial example, further assume particles' exhaust speed (V_Exh) is 10% c. One can express exhaust velocity as a product of decimal component (d_c) and light speed, c.

EXAMPLE: V_Exh = d_c× c = .1 c

Thus, d_c = .1 = V_Exh/ c

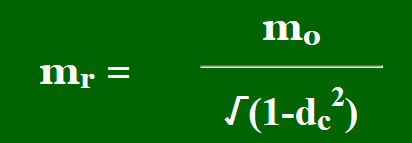
Particle Size

Lorentz Transform quantifies the relativistic growth due to particle speed. Thus, fuel flow per second (ff_sec) is the original mass at rest, and exhaust fuel flow (ff_Exh) is the relativistic mass at an accelerated velocity.

Notional fuel quantity increases per following table.

ff_Exh = n × ff_sec

Original Fuel Flow	Exhaust Velocity	Growth Factor	Exhaust Fuel Flow
ff_sec	V_Exh =d_c×c	n	ff_Exh
1 gm	10% c	1.005	1.005 gm
Given		1 √(1-d_c²)	n×ff_sec

This table shows relativistic mass growth. EXAMPLE: If an exhaust particle accelerates to 10% light speed; then, one gram of fuel will grow 0.5% to 1.005 gm. Subsequent examples consider other quantities at increased exhaust speeds.

II. Assume g-force ...

**Example -2: Assume: V_Exh = 20% c = d_c × c**
**Thus, d_c = .2**
Original Fuel Flow	Exhaust Speed	Growth Factor	Ship Mass
ff_sec	V_Exh = d_c×c	n	M_Ship
1 gm	.2 c	1.0206	6.24 mT
2 gm	.2 c	1.0206	12.48 mT
Given	Given	1 √(1-d_c²)	√(n²-1)×30.57×10⁶ff_sec

Rewrite equation as shown:

M_Ship = (n × ff_sec) × (√(n²- 1) / n × (c/g)

Note decimal component, d_c, defined in terms of n, growth factor.

or d_c = √(n²- 1) / n

c = 299,792,458 m/sec g= 9.80665 m/sec²
c/g = 30,570,323 sec = 30.57 mega-sec

The two constants, light speed (c) and acceleration due to gravity (g) can combine for a third constant (c/g), 30.57 mega-sec. The two "n"s cancel out and the implicit "/sec" of ff_seccancels out the sec from c/g.

M_Ship = √(n²- 1) × 30.57 mega-ff_sec

At the same exhaust speed, the greater the fuel mass, the greater the ship's initial mass that can be increased another 9.8065 m/sec for every second of powered flight (aka "g-force").

...comes from momentum exchange. One second of fuel flow's small mass times enormous speed equals spaceship's huge mass times 9.8065 m/sec velocity increase for one second (happens to equal acceleration due to near Earth gravity, g).

M_Ship × g = ff_Exh × V_Exh

d_c

V_Exh

Define decimal component
of decimal light speed.

√(1 - d_c²)

AXIOMATIC: 'n' = Growth factor.
As if LT's m_o = 1

n²

(1 - d_c²)

Square both sides.

1-d_c²

n²

Rearrange.

d_c²

1 -	1 n²

Rearrange.

d_c²

(n²- 1)

n²

Rearrange.

d_c

√(n²- 1)

Square root both sides.

Both right side terms can be re-expressed. Exhaust fuel mass (ff_Exh) can be rewritten as growth factor, n, times fuel flow per second (n×ff_sec). Particle exhaust velocity (V_Exh) can be rewritten as decimal component times light speed (d_c×c).

M_Ship × g = (n×ff_sec) × (d_c×c)

III. Assume g-force ship's gross weight decreases...

... due to a fairly consistent fuel consumption.
EXAMPLE: If ship's g-force propulsion system consistently consumes 1 gm/sec throughout any given day; then, one could further assume that day's consumption is 86,400 gm.
(1 day = 24 hours × 3,600 sec /hour = 86,400 seconds.) HOWEVER, we don't know exact amount of consistent consumption per second for any given ship; THEREFORE, we can designate that value as a variable, ff_sec.

ff_day = day × ff_sec = 86,400 × ff_sec

Daily % decrease in ship's gross weight can be approximated by the daily decrease divided by ship's GW for that day.

∇=

ff_day

Day × ff_sec×g

ff_sec × √(n²-1) × c

=	Day × g √(n²-1)×c

c =	299,792,458 m/sec
g =	9.80665 m/sec²
Day =	86,400 sec
Day × g /c =	.002826 = .2826%

∇ = .2826% / √(n²-1)

CONCLUSION. Recall that ∇ is daily percentage decrease in vessel's gross weight (GW). Inspection shows that ∇ depends on n (relativistic increase of one second's original fuel flow, ff_o). In turn, n depends on particle speed, d (decimal portion of c, light speed).
It does not depend on actual quantity of consumed fuel nor actual ship's GW.

**Consider ff_Sec and ship's GW.**
Example: **ff_Sec=1.0 gm**
Particle Exhaust Speed	Exhaust Fuel Flow	Ship's Gross Weight	Daily Decrease
V_Exh= d_c×c	ff_Exh=n×ff_sec	GW	∇
0.1 c	1.005 gm	3.072 mT	2.83 %
0.2 c	1.021 gm	6.240 mT	1.41 %
0.3 c	1.048 gm	9.613 mT	0.94 %
Given	ff_sec √(1-d_c²)	ff_sec×√(n²-1)×c g	Day × ff_sec GW

Don't need **ff_Sec** and ship's GW; rewrite as follows:
Decimal Component Light Speed	Relativistic Growth Factor	Daily Decrease
V_Exh= d_c×c	n	∇
0.1	1.005	2.83 %
0.2	1.021	1.41 %
0.3	1.048	0.94 %
Given	1 √(1-d_c²)	.2826% √(n²-1)

IV. Assume ship's range...

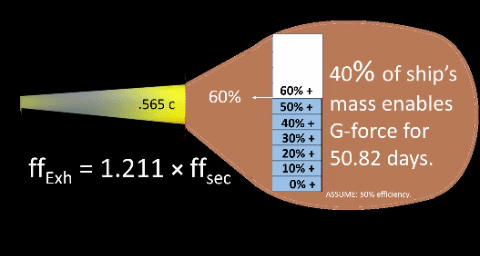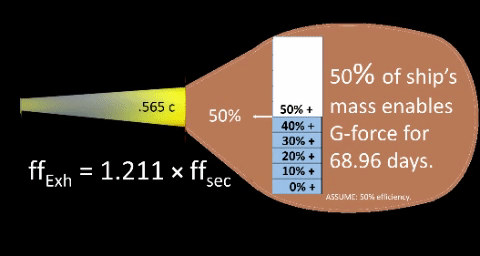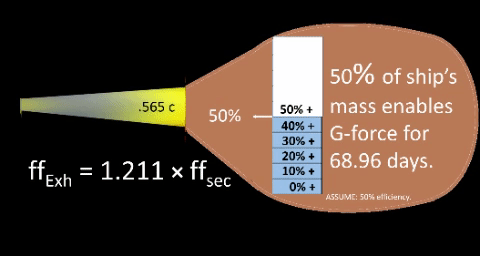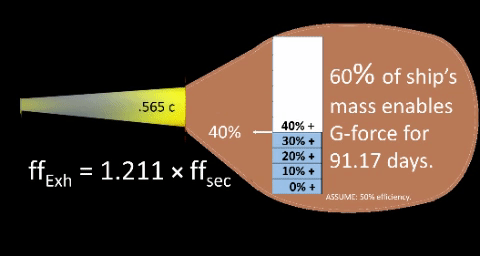
EXAMPLE: Independently vary particle's exhaust speed from 10%c to 60% c. Assume initial fuel load to be 50% of ship's Gross Weight (%TOGW=50%); thus, continuous flow of high speed exhaust particles will decrease ship's weight over a range of days until a minimum gross weight of half of ship's initial GW.
Efficiency factor, ε, enables us to account for inevitable inefficiencies in the propulsion system. Artificially set efficiency factor at 2 (ε = 2.0); thus, TE assumes consumption rate is two times the exhaust flow.
Daily exhaust flow,∇, is the amount of charged particles needed to achieve g-force momentum.
Daily consumption rate. ε∇, is the amount of charged particles needed to ensure required exhaust flow. It accounts for inevitable inefficiencies. AXIOMATIC: ε∇ always exceeds ∇.
Percent Take Off Gross Weight (%TOGW) is the portion of ship's initial mass allocated for fuel.

**APPROX. RANGE: Propulsion Time, t_pLet Percent Take Off Gross Weight (%TOGW) = 50%**
**Let efficiency factor (ε) = 2.0**
Decimal Component Light Speed	Relativistic Growth Factor	Vessel's Propulsion Exhaust Rate	RANGE: Propulsion Time
V_Exh= d_c×c	ff_Exh=n×ff_sec	∇=ff_Day/GW	t_p
.1	1.005	2.81%	11.9 days
.2	1.021	1.41%	24.2 days
.3	1.048	0.94%	36.4 days
.4	1.091	0.71%	48.7 days
.5	1.155	0.57%	60.9 days
.6	1.250	0.47%	73.2 days
Given	1 √(1-d_c²)	.2826% √(n²-1)	log(1-%TOGW) log(1-ε∇)

CONCLUSION. As particle exhaust speed increases, vessel's range increases.

.... can be modeled with daily decrease, ∇, in ship's mass to reflect fuel consumption. Model must also consider efficiency factor, ε, and Percent Take Off Gross Weight, %TOGW.
EXAMPLE: Independently vary ship's %TOGW (portion of ship's mass dedicated to fuel) from 40% to 60%. Assume particle's exhaust speed as constant 56.5% c; then, previous work leads us to determine following values. Decimal component (d_c) is .565; growth factor (n) is 1.211; and daily exhaust flow, ∇, is 0.5% Ship's GW per day.
Efficiency factor (ε) is inverse of efficiency (1/E). For interplanetary performance, Thought Experiment arbitrarily assumes an efficiency of 50%, E=.5; thus, ε = 1/E = 2. (NOTE: There's no way of knowing the actual efficiency of the future g-force propulsion system, but we're sure it's less than 100%.)
Daily exhaust flow,∇. Previous work approximates this value by 86,400×ff_sec divided by ship's current Gross Weight (GW); this reduces to 0.2826% divided by √(n²-1).
Daily consumption rate. ε∇, product of efficiency factor and daily exhaust flow. ε∇ ensures sufficient quantity for daily exhaust. Design flaws and peripheral needs compel a consumption rate greater than exhaust flow.
Percent Take Off Gross Weight (%TOGW). For any given particle exhaust speed, range increases as %TOGW increases. (NOTE: Range is also known as propulsion time (t_p). See following table.)


Ship's Fuel	Exhaust Speed	Growth Factor	Exhaust Rate	Consume Rate	RANGE: Prop. Time
%TOGW	d_c	n	∇	ε∇	t_p
40.00%	0.565	1.211	0.50%/day	1.00%/day	50.82 days
50.00%	0.565	1.211	0.50%/day	1.00%/day	68.96 days
60.00%	0.565	1.211	0.50%/day	1.00%/day	91.17 days
Given	Given	1 √(1-d_c²)	.2826% √(n²-1)	ε×∇	log(1-%TOGW) log(1-ε∇)

Logarithm helps transform %TOGW into available propulsion time.

CONCLUSION. As fuel load (%TOGW) increases, range increases.

V. Assume interplanetary flight profile ....

...such that ship accelerates for half the distance/time and then decelerates for remaining half. Thus, a g-force vessel can use above profile to achieve quickest time for a direct flight from departure to destination. If the ship accelerates further then mid-way; then, ship must decelerate at greater than g-force to achieve orbital speed at destination.
REASON: Maintaining near Earth gravity for the pax and crew is a good thing; thus, ship needs to maintain acceleration rate, g = 9.8 m/sec², for as much of the flight as poss.

Exhaust Vel.	Assume interplanetary envelope up to 50%c for exhaust particles.
Growth..Fact.	Relativistic mass growth affects propulsion performance.
Exhaust Flow	Daily mass (% ship's GW) of high speed particles for g-force.
Range	Use consume rate (ε∇) to determine max days of propulsion time.
Accel. Time	For max acceleration time, divide propulsion time (t_p) by two.
Mid-Velocity	Achieve max velocity at midway. Compute via traditional Newtonian formula.
Accel Dist.	Use traditional Newtonian method to compute distance to max midway.
Total Dist.	AXIOMATIC: If Accel dist. is halfway; then, double to determine max total dist.

**Interplanetary G-force**
**Original fuel flow: ff_sec = 1.0 kg/sec**
**g = 9.80665 m/sec² = .489AU/day²**
Exh. Vel.	Growth Factor	Exh. Flow	Range	Accel Time	Mid. Vel.	Accel Dist	Total Dist
d_c	n	∇	t_p	t_Acc	V_Max	d_Acc	d_Ttl
.10	1.005	2.81%/Day	12.0 day	6.0 day	2.93 AU/dy	8.8 AU	17.5 AU
.20	1.021	1.38%/Day	24.7 day	12.3 day	6.04 AU/dy	37.2 AU	74.5 AU
.30	1.048	0.90%/Day	38.2 day	19.1 day	9.34 AU/dy	89.3 AU	178.6 AU
.40	1.091	0.65%/Day	53.2 day	26.6 day	13.0 AU/dy	172.8 AU	345.7 AU
.50	1.155	0.49%/Day	70.5 day	35.2 day	17.2 AU/dy	303.4 AU	606.9 AU
Given	.1 √(1-d_c²)	.2826% √(n²-1)	log(1-%TOGW) log(1-ε∇)	t_p 2	g×t_Acc	g×t_Acc² 2	2×d_Ac

To g-force to interplanetary, expand ion drive to accelerator drive.

FINAL NOTE-1:	Send AI First. To pave the way for human travelers, precede a human expeditionary force with Artificial Intelligence (AI) devices. AI vessels could forego all the items required to support humans; no food, no air, no entertainment, no social life. Most notable, there is no need to simulate Earth gravity; thus, propulsion could be as great or as small as needed. Communications. One would expect constant streams of data between Earth and this vessel, but interactions must delay due to light speed limitation. If a vessel is one AU away; signal will take at least 8 min to reach the vessel, and another 8 min for the response to reach original sender. For 10 AU, signal will take about 83 minutes between vessels and 166 mins for a two way response. Thus, two way communications will become extremely difficult; immediate responses will become impossible. Autonomy will be compelled by such communications. Thus, a robotic "pathfinder" vessel will need to be extremely sophisticated, because such systems will prove essential.
FINAL NOTE-2:	Even an pessimistic g-force profile to the Kuiper Belt (beyond the planets) takes weeks. However, the Solar System extends well beyond Kuiper; some say it extends a full LY from Sol out to the Oort Cloud. Particle exhaust speeds of 0.5 c will fall far short of getting us that far; we'll need an expanded envelope to truly explore entire Solar System not to mention visit neighbor stellar systems.
CONCLUSION: Push the particle envelope, accelerate ions much closer to light speed.

SLIDESHOW

VOLUME 0: ELEVATIONAL
VOLUME I: ASTEROIDAL
VOLUME II: INTERPLANETARY
VOLUME III: INTERSTELLAR

A Thought Experiment

Tuesday, February 10, 2009

PUSH PARTICLES TO INTERPLANETARY

0 Comments:

About Me

Previous Posts