PUSH TOWARD INTERSTELLAR
TE assumes an interstellar exhaust velocity (VExh) of at least 86.6% light speed, .866 c. Thus, as exhaust velocity approaches every closer to c; spaceship range increases. When we achieve this; interstellar flights will become feasible. However, for interstellar flights to become practical, we must overcome significant problems.
---Reliability becomes ever more important for interstellar voyages. Precise quantities of near light, exhaust particles must exit vessel for every second of every day.
---Flight duration expands by several orders of magnitude. Exhaust particles must maintain near light speeds for years while interplanetary need only days of much slower exhaust speeds.
---Flight duration expands by several orders of magnitude. Exhaust particles must maintain near light speeds for years while interplanetary need only days of much slower exhaust speeds.
| EXPAND ENVELOPE | |
|---|---|
| from INTERPLANETARY particle accelerator | ... will transform several grams/sec of water to ions and expel them at speeds from 10% to 50%c. This will produce equivalence and quick flights to nearby planets (days to weeks). |
| to INTERSTELLAR particle accelerator | ... will transform several kilograms/sec of water to ions and expel them at growth factors from 2 to 11 (i.e. corresponding particle exhaust velocities of 86.6%c to 99.6%c). This will produce g-force acceleration for lengthy durations from 100 days to over a year.. |
...can consume reasonable quantities of fuel particles, original fuel flow per second (ffsec), and accelerate them into a constant flow of exhaust particles (ffExh). 
For this initial example, further assume particles' exhaust speed (VExh) is 86.6% c. One can express exhaust velocity as a product of decimal component (dc) and light speed, c.
EXAMPLE: VExh = dc × c = .866 c
Thus, dc = .866 = VExh / c
| mr = | mo √(1-dc2) |
|---|
Particle Size
Lorentz Transform quantifies the relativistic growth due to particle speed. Thus, fuel flow per second (ffsec) is the original mass at rest, and exhaust fuel flow (ffExh) is the relativistic mass at an accelerated velocity.
Notional fuel quantity increases per following table.
ffExh = n × ffsec
| Original Fuel Flow | Exhaust Velocity | Growth Factor | Exhaust Fuel Flow |
|---|---|---|---|
| ffsec | VExh =dc×c | n | ffExh |
| 1 kg | .8667c | 2.0 | 2.0 kg |
| Given | 1 √(1-dc2) | n×ffsec | |
| Original Fuel Flow | Exhaust Speed | Growth Factor | Ship Mass |
|---|---|---|---|
| ffsec | VExh = dc×c | n | MShip |
| 1 kg | .943 c | 3 | 83,623 mT |
| 2 kg | .943 c | 3 | 173,246 mT |
| Given | Given | 1 √(1-dc2) | √(n2-1)×30.57×106ffsec |
| dc | = | VExh/c |
|---|---|---|
| n | = | 1/√(1-dc2) |
| n2 | = | 1/(1-dc2) |
| 1-dc2 | = | 1 / n2 |
| dc2 | = | 1 - (1 / n2) = (n2 - 1) / n2 |
| dc | = | √(n2 - 1) / n |
| MShip × g = ffExh × VExh |
|---|
| MShip × g = (n×ffsec) × (dc×c) |
|---|
| MShip = (n×ffsec) × (√(n2 - 1) / n×(c/g) |
|---|
c/g = 30,570,323 sec
| MShip = √(n2 - 1) × 30.57 mega-ffsec |
|---|
(One day = 24 hours × 3,600 sec /hour = 86,400 seconds.)
| ffday =day × ffsec =86,400 × ffsec |
|---|
|
|---|
c =
|
299,792,458 m/sec
|
|---|---|
g =
|
9.80665 m/sec2
|
Day =
|
86,400 sec
|
| Day × g /c = | .002826 = .2826% |
Conclusion: Inspection shows daily decrease depends on particle size, n (multiple of original ffo), which depends on particle speed, d (decimal portion of c, light speed).
THUS, vessel's range depends:
- not on actual quantity of ffsec
- nor actual ship's gross weight, GW.
| Particle Exhaust Speed | Exhaust Fuel Flow | Ship's Gross Weight | Daily Decrease |
|---|---|---|---|
| VExh= dc×c | ffExh=n×ffsec | GW | ∇ |
| .866 c | 2.00 kg | 52,949 mT | 0.16 % |
| .943 c | 3.00 kg | 86,465 mT | 0.10 % |
| .968 c | 4.00 kg | 118,397 mT | 0.07 % |
| Given | ffsec √(1-dc2) | ffsec×√(n2-1)×c g | Day × ffsec GW |
| Relativistic Growth Factor | Decimal Component Light Speed | Daily Decrease |
|---|---|---|
| n | dc | ∇ |
| 2 | .866 | 0.16 % |
| 3 | .943 | 0.10 % |
| 4 | .968 | 0.07 % |
| Given | √(n2-1) n | .2826% √(n2-1) |
Efficiency, (E), will likely improve as humanity learns to design better g-force propulsion systems. Assume inefficiency (E') decreases with growth factor, n; perhaps, E'=.5×.9n-2. Subsequently, Efficiency (E) will increase (1-E'); efficiency factor (ε = 1/E) will decrease.
Daily exhaust flow,∇, is the amount of charged particles needed to achieve g-force momentum.
Daily consumption rate. ε∇, is the amount of charged particles needed to ensure required exhaust flow. It accounts for inevitable inefficiencies. AXIOMATIC: ε∇ always exceeds ∇.
Percent Take Off Gross Weight (%TOGW) is the portion of ship's initial mass allocated for fuel.
| Relativistic Growth Factor | Decimal Component Light Speed | Vessel's Propulsion Exhaust Rate | Forecast Efficiency Factor | RANGE: Propulsion Time |
|---|---|---|---|---|
| ffExh=n×ffsec | VExh= dc ×c | ∇=ffDay/GW | ε | tp |
| 2 | .866 | 0.163% | 2.000 | 212 days |
| 3 | .943 | 0.100% | 1.818 | 381 days |
| 4 | .968 | 0.073% | 1.681 | 565 days |
| 5 | .980 | 0.058% | 1.574 | 763 days |
| 6 | .986 | 0.048% | 1.488 | 975 days |
| 7 | .990 | 0.041% | 1.419 | 1,197 days |
| Given | √(n2-1) n | .2826% √(n2-1) | 1 1 -(.5×.9n-2) | log(1-%TOGW) log(1-ε∇) |
CONCLUSION. As particle exhaust speed increases,
vessel's range increases.
vessel's range increases.
EXAMPLE: Independently vary ship's %TOGW (portion of ship's mass dedicated to fuel) from 40% to 60%. Assume particle's exhaust speed as constant 99.0% c; then, previous work leads us to determine following values. Decimal component (dc) is .990; growth factor (n) is 7; and daily exhaust flow, ∇, is 0.041% Ship's GW per day.
Efficiency factor (ε) is inverse of efficiency (1/E). For interstellar performance, Thought Experiment arbitrarily assumes an efficiency model: ε = 1/E = 1/(1-.5×.9n-2). (NOTE: There's no way of knowing the actual efficiency of future g-force propulsion systems, but we're sure their efficiency will improve.)
Daily exhaust flow,∇. Previous work approximates this value by dividing .2826% by the term, √(n²-1).
Daily consumption rate. ε∇, product of efficiency factor and daily exhaust flow. ε∇ ensures sufficient quantity for daily exhaust by consuming more sure than needed. Design flaws and peripheral needs will compel a consumption rate greater than exhaust flow.
Percent Take Off Gross Weight (%TOGW). For any given particle exhaust speed, range (R) increases with %TOGW. (See following table.)
| Ship's Fuel | Exhaust Speed | Growth Factor | Exhaust Rate | Consume Rate | RANGE: Prop. Time |
|---|---|---|---|---|---|
| %TOGW | dc | n | ∇ | ε∇ | tp |
| 40.00% | 0.866 | 2 | 0.163%/day | .326%/day | 156.3 days |
| 50.00% | 0.866 | 2 | 0.163%/day | .326%/day | 212.1 days |
| 60.00% | 0.866 | 2 | 0.163%/day | .326%/day | 280.3 days |
| Given | Given | 1 √(1-dc2) | .2826% √(n2-1) |
∇
1-(.5×.9n-2) |
log(1-%TOGW)
log(1-ε∇) |
CONCLUSION. As fuel load (%TOGW) increases,
vessel's range increases.
vessel's range increases.
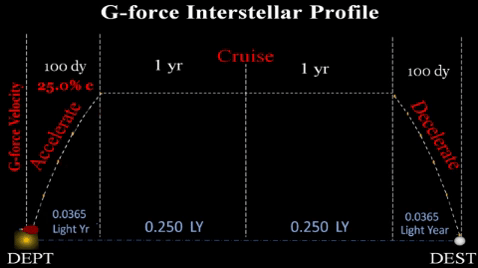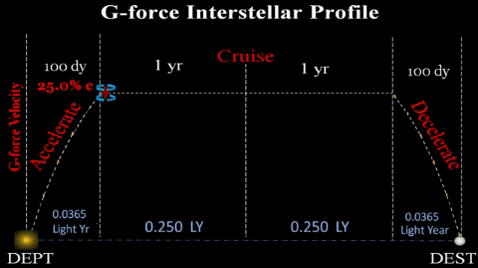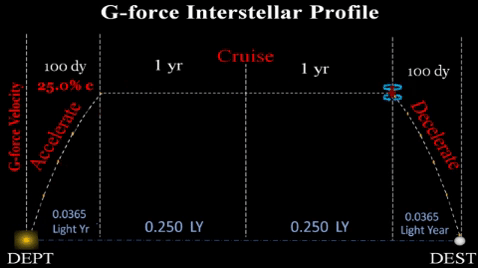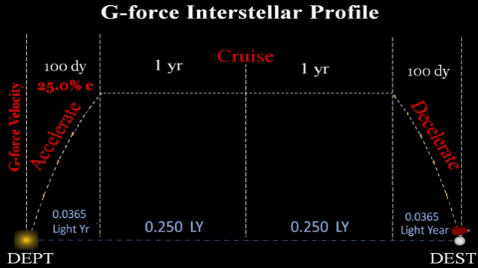
...such that ship accelerates for 100 days, cruises at constant speed for several years, and then decelerates for last 100 days of voyage.
REASON: To maintain Earth-like gravity (g-force) for the pax and crew throughout the multi-year voyage, the vessel must: 1) accelerate via a high speed ion propulsion -or- 2) during constant velocity cruise, spin the vessel longitudinally.
Initially, ship uses ion stream to accelerate at g:
g = 9.80665 m/sec² = 0.489 AU/day² = g
for a feasible duration (at least 100 days). Even after a year of such g-force, ship will be far short of midway between any two stars. However, TE assumes initial technology will limit vessel range for first few star ships for about 100 days of acceleration; thereafter, it must then cruise at constant velocity (approx .25 c) until it reaches the deceleration point 100 days prior to destination. During cruise, it must change into a habitat (roughly cylindrical shape) and spin about its longitudinal axis at an exact angular velocity to produce centrifugal g-force at inside of outer hull. At deceleration point, ship will again emit ion streams to slow vessel.
Initially, ship uses ion stream to accelerate at g:
| Growth Factor | At relativistic speeds, particle grows by multiple, n. |
| Particle Velocity | Each multiple, n, maps to a specific, relativistic speed (vExh). |
| Exhaust Flow | To achieve g-force acceleration, ship must consistently expel numerous high speed particles which collectively decrements ship's GW, expressed as a daily percentage. |
| Consume Rate | Due to inevitable inefficiencies, consumption rate (ε∇) must exceed exhaust flow as determined by an Efficiency Factor (ε). |
| Prop. Time | Total of 200 days. TE assumes initial interstellar vessels will g-force accelerate for 100 days, cruise for years; then, g-force decelerate for 100 days; thus, total propulsion time would be 200 days. |
| Accel. Time | Divide propulsion time (tp) by 2; thus, 200 days/2 = 100 days. |
| Max-Velocity | TE assumes 100 days of g-force produces cruise velocity of about .25c derived from exponential (t) as shown. Vt = c(1-(1-Δ)t) For more.... |
| Accel Distance | TE assumes 100 days of g-force travels about .0353 LY, derived from natural logarithm. d = c×t + V/ [ln(1-Δ)]. For more.... |
| Gro. Fact. | Part. Vel. | Exh. Flow | Effic. Factor | Cons. Rate | 200 Day Cons. |
|---|---|---|---|---|---|
| n | vExh | ∇ | ε | ε∇ | %TOGW |
| 2 | .866 c | .163% day |
2.00 | .326% day | 47.99% |
| 3 | .943 c | ,100%/Day | 1.818. | .182%/Day | 30.49% |
| 4 | .968 c | .073%/Day | 1.681. | .123%/Day | 21.76% |
| 5 | .980 c | .058%/Day | 1.574. | .091%/Day | 16.61% |
| 6 | .986 c | .048%/Day | 1.488. | .071%/Day | 13.26% |
| 7 | .990 c | .041%/Day | 1.419 | .058%/Day | 10.93% |
| 8 | 992 c | .036%/Day | 1.362 | .048%/Day | 9.24% |
| 9 | 994 c | .032%/Day | 1.314 | ..042%/Day | 7.97% |
| 10 | 995 c | .028%/Day | 1.274 | .036%/Day | 6.98% |
| 11 | .996 c | .026% day |
1.24 | .032% day | 6.2% |
| Given | √(n2-1) n | .2826% √(n2-1) | 1 1 -(.5×.9n-2) | ε × ∇ | 100%-(1-ε∇)200 |
FINAL NOTE-1:
|
Send Robots First. To pave the way for human travelers, precede a human expeditionary force with robotic explorers. With only Artificial Intelligence (AI) occupants, a vessel could forego all the items required to support humans; no food, no air, no entertainment, no social life. Most notable, there is no need to simulate Earth gravity; thus, propulsion could be as great or as small as needed.
Communications. One would expect constant streams of data between Earth and this vessel, but interactions must delay due to light speed limitation. (i.e., if a vessel is one light year away; signal will take at least a year to reach the vessel, and another year for the response to reach original sender.) Autonomy will be compelled by communication circumstances. Thus, a robotic "pathfinder" vessel will need to be extremely sophisticated, because such systems will prove essential. With a plethora of stellar systems to choose from, robots must explore all prospective destinations to provide data for humanity to choose best prospects of which planets to visit first. |
FINAL NOTE-2:
|
Even an optimistic flight profile to the nearest star system, Alpha Centauri (AC), would take several years.
Thus, a 50%TOGW fuel load could easily be completely consumed; this leads to following flight plan options: 1) One-way mission with no chance of returning to Earth. Vessel occupants would resign themselves and their descendants to orbit AC indefinitely in their spaceship. 2) In situ materials. Gather AC indigenous comets for fuel for return trip. This is one of many areas where the robotic pathfinder would prove its worth; they could survey the system for comet availability. 3) Very high exhaust speeds. Particle speeds in excess of .999c would result in growth factors of eleven and higher. Thus, a 50%TOGW fuel load could accommodate four fuel burns of one year each. Thus, a vessel could g-force for one year for initial acceleration to AC, cruise for a few years, g-force for final year to decelerate just prior to AC. For return trip, vessel could again accelerate for a year, cruise for a while; finally, decelerate just prior to Sol, Earth's sun. |
| CONCLUSION Push the particle envelope, push exhaust speed closer to c. | |
|---|---|
posted by JimODell at 2:06 AM
0 Comments:
Post a Comment
<< Home