TO NEIGHBOR STARS
Alpha Centauri (AC) is Sol's nearest neighbor.
AC is a cluster of three stars about 4.3 light years (LYs) away.
Our thought experiment notionalizes an interstellar spaceship with an particle accelerator propulsion system which constantly accelerates the vessel at g-force. Such a spacecraft could get us to nearby planets within days AND also simulate near Earth gravity throughout the trip; but interstellar travel would take much longer.
Recall that interplanetary trips require following g-force profile . ---G-force accelerate for a few days to the midpoint of the trip. ---Precisely at midpoint, reverse direction of spacecraft so the ship's exhaust vectors now points opposite direction of flight. ---G-force decelerate for the remaining half of journey until ship reaches destination. Thus, after one day of g-force travel, a vessel could achieve velocity of 847.8 kilometers per second (kps) about .283 percent of the speed of light, c.
Interstellar travel requires a new profile. Consider following points: 1. Acceleration to Midpoint is impractical. Interplanetary distances are just a few AUs; thus, g-force acceleration will take just a few days. However, midpoint to the nearest star, AC, is over 2 LYs, over 120,000 AUs; this takes years of g-force propulsion which could easily consume the ship's weight in fuel. 2. Interstellar G-force Velocities approach c, light speed. In contrast, interplanetary g-force flights never even approach c. EXAMPLE: G-force flight to Mars will typically require less than 3 days of acceleration for max velocity less then 1%c. 3. Special Relativity Theory maintains that any observer always measures c at 299,792 kps regardless of observer's own velocity. Numerous published works in both theory and experiment continue to confirm that no object with mass can exceed c; but continuing acceleration will take you closer and closer to that relativistic limit. Consider cases where a g-force vessel accelerates for 100 days, 200 days or any number of days. After any given duration, let the g-force vessel release a module with no propulsion; that module stops accelerating and maintains velocity at time of release. An occupant on that module will observe the g-force vessel accelerating away; as a matter of fact, TE assumes the module observer will always observe a velocity increase of .283%c after an additional day has elapsed. |  A year of constant g-force acceleration can achieve significant fraction of light speed.For longer durations, "t × g" no longer works. EXAMPLE: After one year of g-force propulsion, V1Year= 365.25 days ×Δ = 1.033c, an impossibility!!! Resulting velocity exceeds c, which contradicts Einstein's Special Theory of Relativity. Thus, previous work proposes the Remainder (R) concept to determine g-force velocities. After one day, an Earth bound observer measures g-force vessel velocity at .283%c with remaining velocity of 99.717%c till the speed of light. Thus, R = c (1-Δ). After any given number (n) of g-force days of travel, above module is released. After another day (n+1), TE assumes that module occupant will observe g-force vessel increase velocity to .283%c with a R of 99.717%c until light speed. Furthermore, TE assumes that Earth bound observer can use Remainder (R) exponentials to predict velocity for any number of g-force days. Following table predicts vessel velocity after one year (365.25 days) of g-force.
EXAMPLE: After one year of g-force propulsion,
an Earth bound observer measures velocity of 64.5% c. | ||||||||||||||||||||||||||||||||||||||||
For Interplanetary Destinations:
Traditional Newtonian Agrees with Relativistic Einsteinian
Newton formulas: Vt = t × Δ and dt = t × g work well for the special case of extremely slow velocity, the portion of the speed spectrum where humanity lives.
EXAMPLE: For a trip to Mars, a vessel might need two days of g-force acceleration to reach midway of the journey. After two days of g-force propulsion, interplanetary g-force spaceship velocity is still less then 1% of light speed.
Vt = 2 days × .283%c/day = .566c
We see the Einsteinian velocity formula Vt = c [1-(1-Δ)t] gives almost the same velocity for two days of g-force.
V2 = c [1-(1-.002826)2] = 0.564%c
ANOTHER EXAMPLE: A Kuiper Belt Object (KBO) destination might need 10 g-force days to reach midpoint.
|
For Interstellar Destinations:
Traditional Velocity Values Diverge from Relativistic
If we expand g-force duration from days to years, we see a wide divergence between Newton and Einstein.
After one year of g-force acceleration, we see following difference:
Newtonian value is clearly wrong; nothing exceeds c.
Previous work leads TE to the Einsteinian method. 
After two years of g-force acceleration, we see greater difference:
Newtonian is clearly wrong; vessel cannot exceed light speed. Previous work leads TE to assume Einsteinian method produces a reasonable g-force velocity.
|
| G-force acceleration to the midpoint between stars would take too long; a starship would easily consume well over 100% of its mass in fuel during the multi-year voyage.
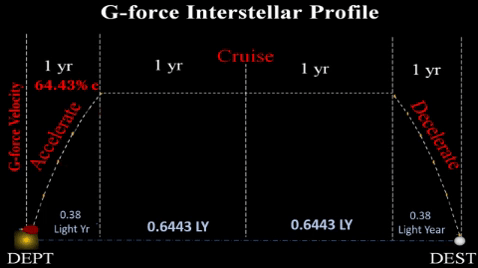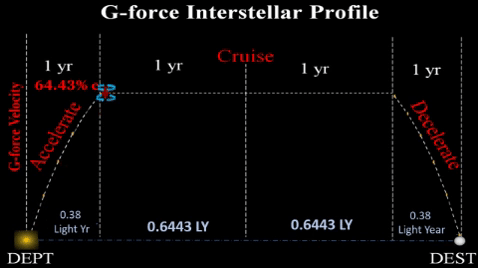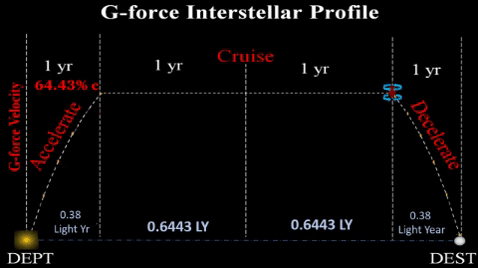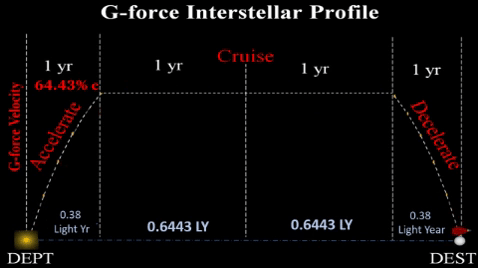
Thus, interstellar flights need three phases:
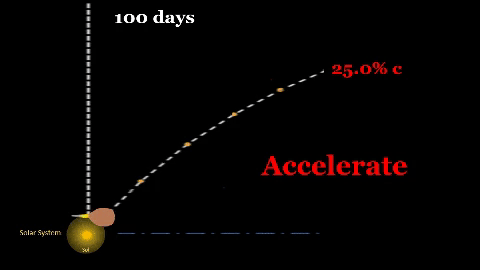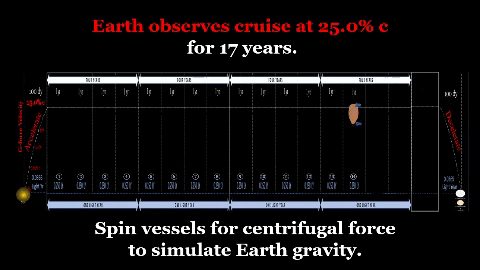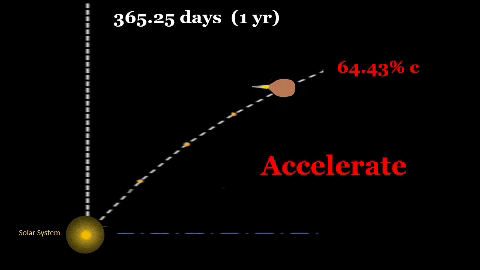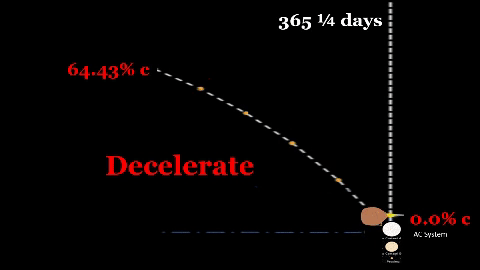
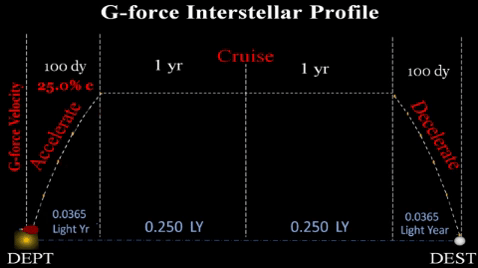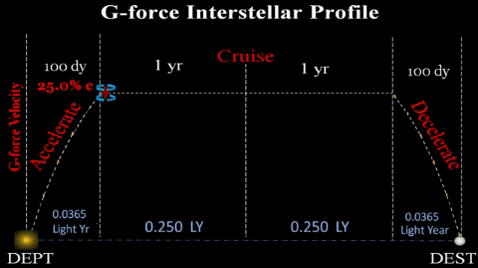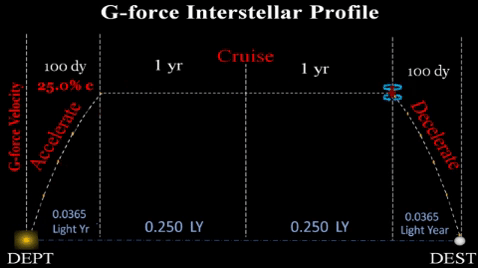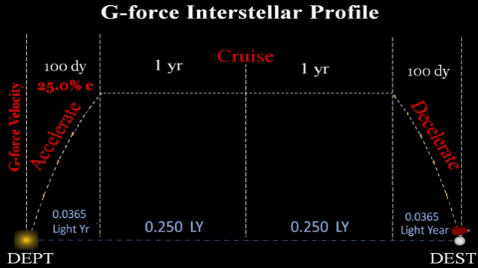 1) ACCELERATION brings ship to a near light speed velocity which facilitates a reasonable cruise duration. If our spaceship accelerates at g-force for 100 days;
It will consume perhaps 25% of available fuel (depending on design efficiencies and exhaust particle velocity). However, acceleration distance
2) CRUISE. Interstellar flights will need a lengthy constant velocity duration to conserve fuel. This profile assumes a cruise phase at .6c for several years. Earth bound observers will see the cruise portion take several years; but onboard crew and passengers will observe the trip taking much less time due due to relativistic time dilation. Maintaining Earth-like environment will be very important during this multi-year period; however, humans will have been living in asteroidal habitats (which rotate to simulate Earth gravity) for many decades and probably generations prior to going interstellar. Thus, going interstellar will require some midflight reconfiguration for the cruise portion. 3) DECELERATION. About .0365 LY from destination, spaceship must decelerate from .25 c to an operational velocity. Assuming consistent g-force, this will take same duration as the acceleration phase (100 days) and another large portion of fuel. |
Propulsion time sums durations for acceleration (tAcc) and deceleration (tDec); propulsion needs fuel to apply g-force. However, cruise duration is excluded since no propulsion is applied during this lengthy phase. TRADEOFFS. Duration of 100 days for acceleration/deceleration was chosen arbitrarily. Flight planners can choose any duration as long as they observe the tradeoffs between fuel availability and total trip time.
Consider following interplanetary flight assumptions:
Simulate Earth Gravity Throughout Voyage.
During g-force acceleration, a spaceship can attain enormous speeds and simulate earthlike gravity.
During cruise portion of voyage, vessel simulates gravity via centripetal force due to spin about its longitudinal axis (same as asteroidal habitats throughout the Solar System).
For final portion of flight, the vessel must use g-force to decelerate for same time/distance as for acceleration phase.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Definitions
1) D is observed or given distance from our star, Sol, to destination2) tAcc is duration of acceleration from departure till start of cruise. This case study chooses one year (365.26 days) for all destinations. 3) Δ - Daily difference in spaceship's velocity is due to acceleration caused by constant g-force. We approximate this value:
Δ = 86,400sec/day × g / c = .2826% c/day
g = 9.8065 m/sec² & c = 299,792,458m/sec
4) VFin is final velocity achieved after applying g-force propulsion for given duration (tAcc). ---VFin is the max velocity achieved during the flight. ---VFin is also cruise velocity; for this case study, it is .6443 c for all examples. 5) dAcc is acceleration distance; this case study uses .38 LY for all examples.
1 light year (LY) = 63,241 AU
6) dDec is deceleration distance, distance needed to slow down from max velocity to operational velocity at destination. Same distance as acceleration distance (.38LY). 7) dCru is cruise distance; total dist. (D) minus dist. for acceleration (dAcc) and deceleration (dDec). 8) tCru is cruise time as observed from the Earth. 9) tDec is deceleration time. Given consistent g-force, assume deceleration time equals acceleration time. 10) T is total time: acceleration + cruise + deceleration. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
SUMMARY
AXIOM. Light speed is absolute; this limits velocity on interstellar travel. Even at light speed, interstellar flights take years for photons, virtually massless particles. Since human space ships will contain large quantities of mass, the best we can hope for is to approach light speed; we can never attain it and certainly never surpass it. |  |
|---|
ASSUMPTION-1. Self Contained Fuel. Prior to departure, notional spaceship will collect and carry sufficient fuel for planned propulsion durations: acceleration (tAcc) and deceleration (tDec).
ASSUMPTION-2. Earthlike Gravity. We currently know two methods to achieve Earth like gravity on an interstellar vessel. 1) Constant G-force Acceleration. If an onboard propulsion system can change ship's velocity by 9.80665 m/s for every second of "powered" flight'; then, ship's contents will feel a force equivalent to Terran gravity. 2) Centrifugal Force. During non-powered cruise phase, the g-force alternative is a carefully controlled spin to generate g-force by 'pressing' contents against the inside of the outer hull. If ship was cylindrical in shape and rotated around its longitudinal axis; spin rate (degrees per second) will be inversely proportional to radius (as cylinder size increases, less spin rate is needed to maintain centripetal acceleration of 9.80665 m/s/s). | ASSUMPTION-3. Three Phases. Initial calculations indicate that a vessel powered throughout entire interstellar voyage could easily consume fuel greater than ship's total mass. Thus, TE assumes following flight profile. 1) Acceleration Phase. Ship starts off trip by accelerating at g-force for 365.26 days, this will bring it to a velocity of .6443c (64.43% of light speed). Occupants will feel an Earth like gravity holding them "down". 2) Cruise Phase. Due to fuel considerations, ship will stop propulsion after 1 year to stop the g-force. Thus, ship will maintain constant velocity of 64.43c for entire cruise phase (majority of voyage). To maintain Earth like gravity, ship will then reconfigure to gain g-force against inside of outer hull by starting sufficient spin to gain g-force. 3) Deceleration Phase. At 1 year prior to end of voyage, ship will restart g-force propulsion. This will slow down vessel from 64.43% c to achieve an operational speed upon arrival at the destination stellar system. Thus, vessel occupants will feel same g-force rate as during acceleration phase. |
| VOLUME 0: ELEVATIONAL |
|---|
| VOLUME I: ASTEROIDAL |
| VOLUME II: INTERPLANETARY |
| VOLUME III: INTERSTELLAR |
posted by JimODell at 2:17 AM
0 Comments:
Post a Comment
<< Home