LEVERAGING LAMBDA (ℓ) for Cyclers

Greek lambda is usually shown in lower case Greek, λ,  or upper case, Λ.  However, in Kepler's lifetime, scientists often used cursive lambda (ℓ) to represent semi-latis rectum, an essential component of the ellipse. 
BACKGROUND: Recall basic parts of ellipse: semi-major axis (a), longest ray from center to border, and semi-minor axis (b) shortest such ray.

DESCRIBE SEMI-LATIS RECTUM: lambda(ℓ)
The focus is another essential component of the ellipse.  Distance from center to focus, c, has a Pythagorean relationship with a and b as shown in following diagram.  In the Solar System, all orbits have an elliptical shape, and Sol, our sun, is at one of the two foci.	Semi-latis rectum (ℓ) is defined as an ray perpendicular to major axis which extends from a focus to border of ellipse.  Since an ellipse has.two foci, it has four semi-latis rectums. Component, ℓ, will play a key role in this chapter.
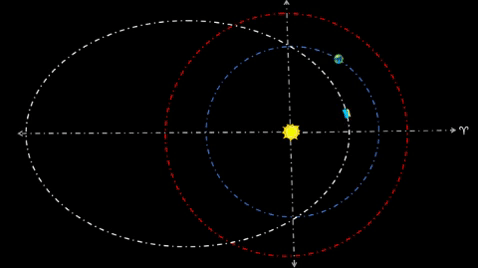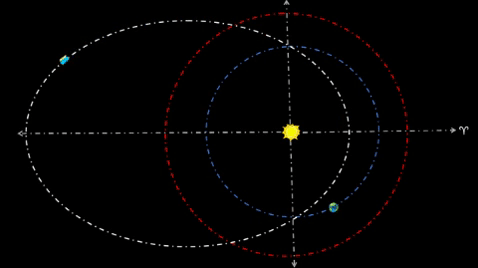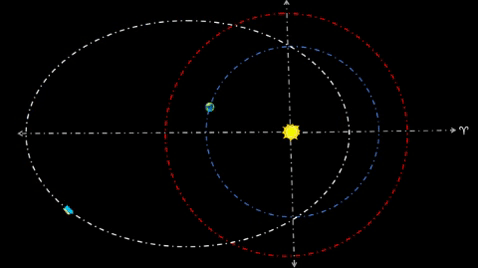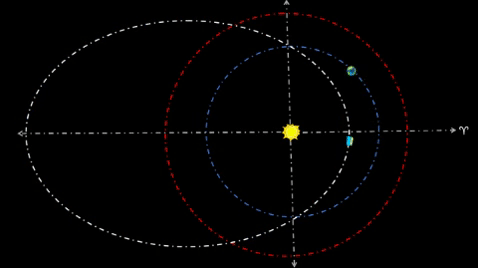
FIRST CYCLER TRAVELS TWO YEAR ORBIT
Align orbit such that its perihelion (q) is on Vernal Equinox, and q is .623 AU from Sol (well inside Terra's Solar orbit).  Orbit's reference ray (t=0 days) commonly extends from Sol to q.  For Period (P) to be two years, Kepler's 3rd Law requires semi-major axis (a) to be 1.58 AU.  In turn, semilatis rectum (ℓ) will be 1.0 AU; in fact, the cycler orbit (assume zero inclination) will intercept Earth's orbit at two distinct semilatis rectum (ℓ1 and ℓ4). Time increments for positions around q indicate quicker speeds due to proximity of Sol. On the other hand, much longer time increments for positions around Q indicate much slower speeds due to greater distance from Sol. EXAMPLE: Distance from q to ℓ1 is same as from Q to ℓ3; however, orbit time from q to ℓ1 is 50.6 days while orbit time from Q to ℓ3 is 161.25 days which is much longer. For detailed orbit times, see Two Year Table.
HABITAT ALPHA (α) LEADS EARTH
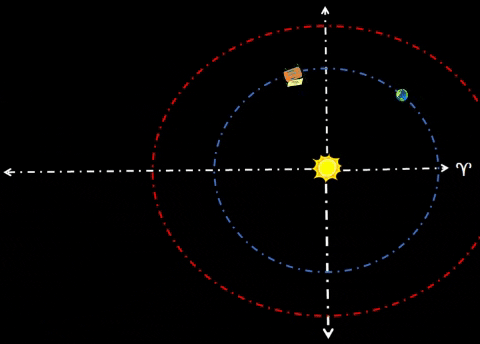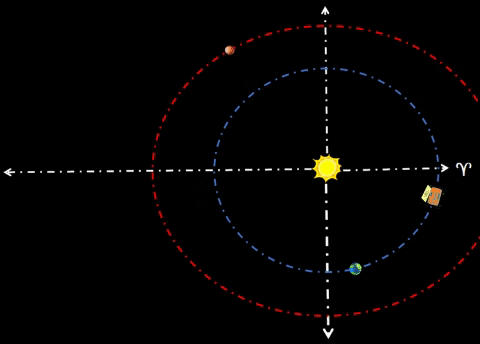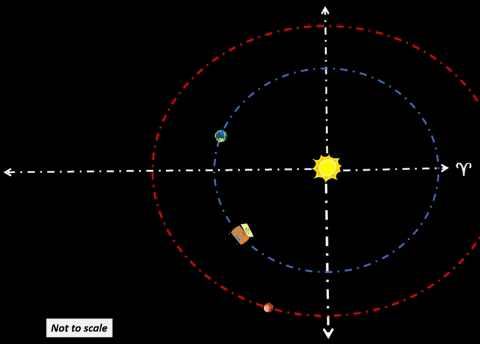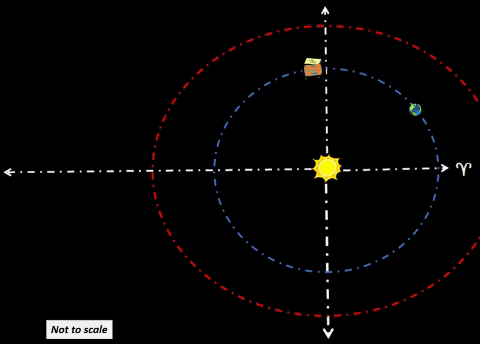	Habitat  α will lead Terra by 60°. This habitat could be safe haven for receiving resources from cycler missions. Purpose.  Cyclers could harvest asteroids/comets throughout the Solar System and bring them to Earth for final processing.  To reduce risk of impacts to either Terra or Luna, one should place these payloads well away from Mother Earth; in this instance, Hab-α would be 1 AU from Earth. Alpha colony could process cycler payloads at a safe distance from Terra, their Home Planet. At 1.0 AU from Earth, Hab-α could safely harvest resources from far corners of the Solar System. 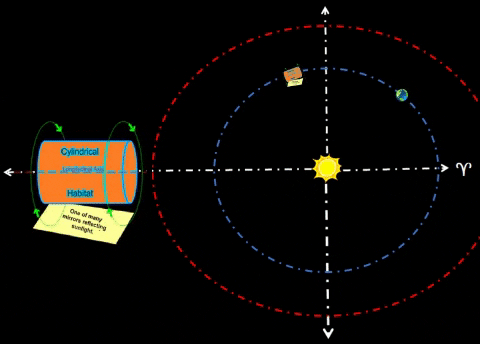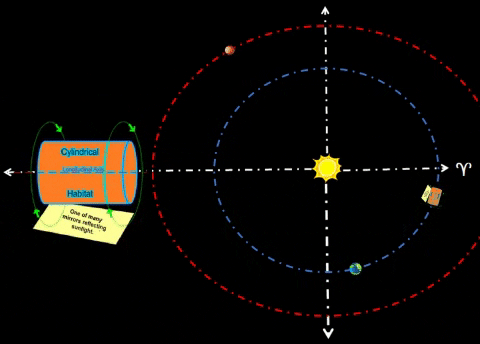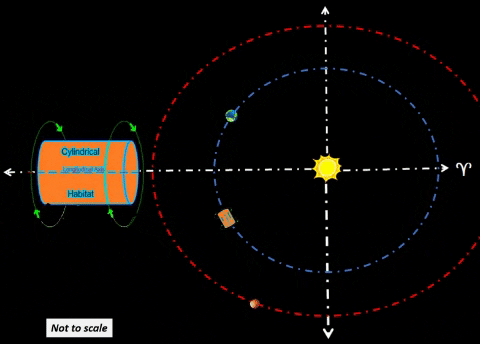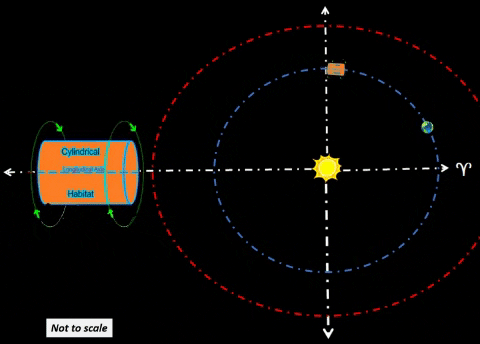Exterior Mirror Rotates About Habitat. Solar radiation provides plentiful supply of energy.
ADD 2ND CYCLER; SYNC CYCLERS WITH ALPHA
Synchronize Cycler-1 to intercept Habitat-α at Winter Solstice (WS) as shown in diagram. Synchronize Cycler-2 to intercept Habitat-α at Summer Solstice (SS); thus, Cycler-2 lags Cycler-1 by 81.5 days when Cycler-1 is at WS. Note time tags for all objects at three distinct times: t=0 days: Cycler-1 and Habitat-α are both at WS.  Cycler-2 lags Cycler-1 as shown. t=91.3 days:  After 3 months, Habitat-α arrives at Vernal Equinox. However, Cycler-1 is well ahead (due to traveling a path much nearer to Sol).  Earth continues to lag Habitat-α by 60°.  Cycler-2 is gaining. t=182.6 days:  Cycler-2 and Habitat-α are both at SS.  Cycler-1 leads Cycler-2 as shown.
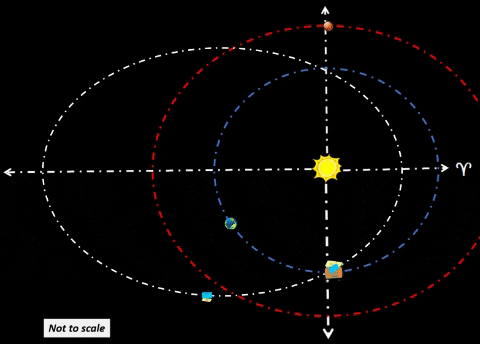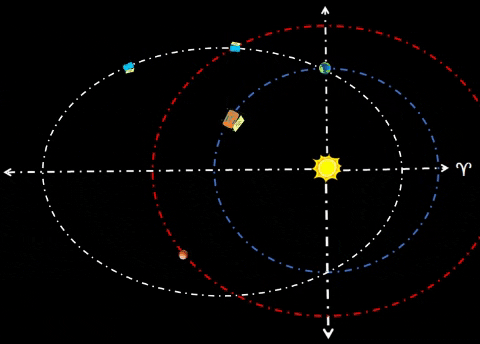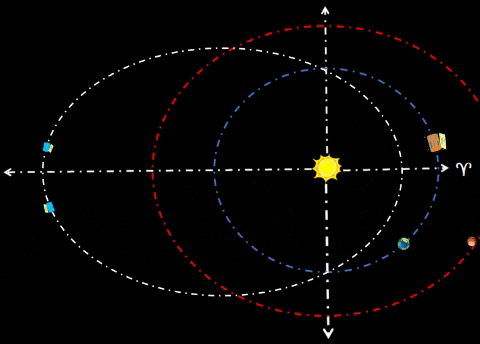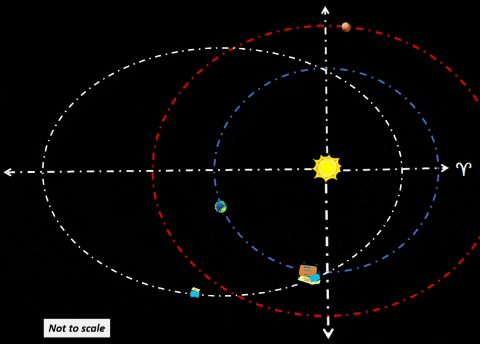ADD HABITAT OMEGA (Ω)
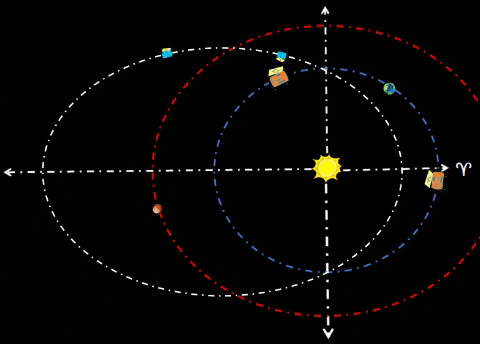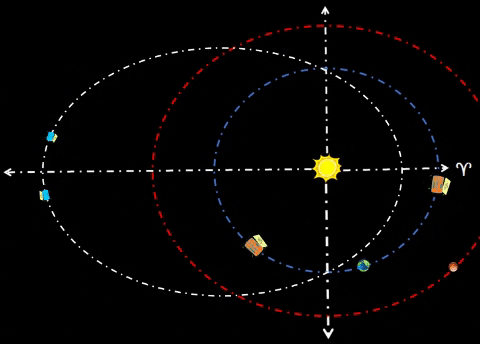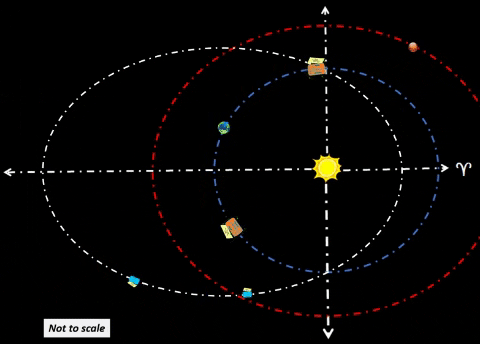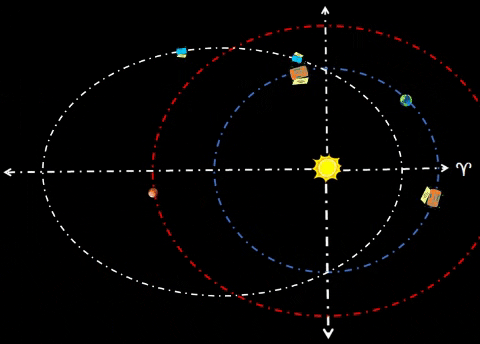	Habitat Ω could lag Earth by 60°.  Both habitats α and Ω could be safe havens for receiving resources from cycler missions. Purpose.  Cyclers could harvest asteroids/comets throughout the Solar System and bring them to Earth for final processing.  However, huge chunks of extraterrestrial material entering orbits around Earth presents some impact risk.  To mitigate enormous risk, place these habitats well away from Mother Earth; in this instance, both are 1 AU from Earth. Omega/Alpha colonies could process cycler payloads at a safe distance from Terra, their Home Planet. At 1.0 AU from Earth, these habitats could safely harvest resources from far corners of the Solar System.
ADD CYCLERS 3 & 4
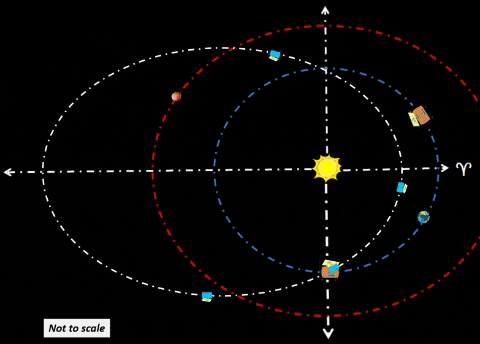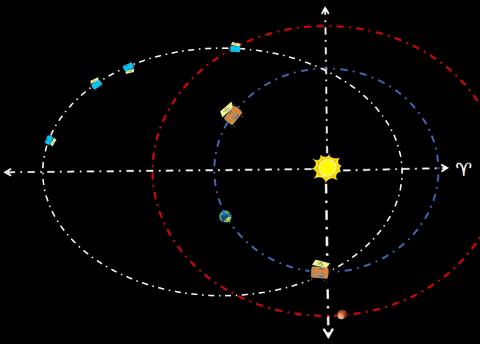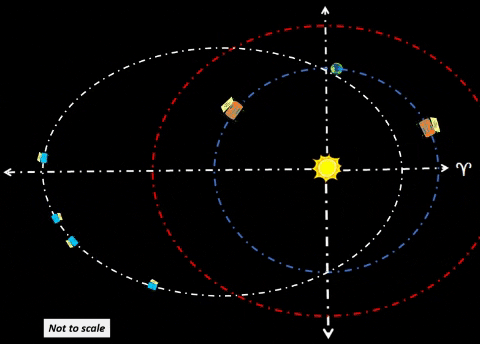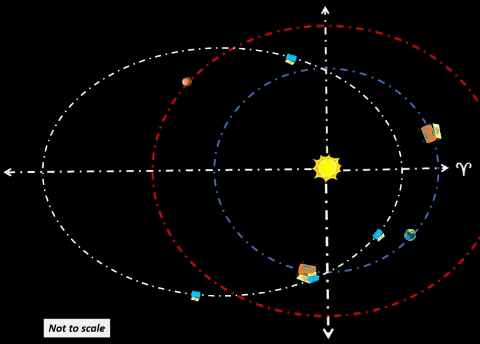	Synchronize Cycler-3 to intercept Habitat-Ω at WS as shown in diagram; later, Cycler-4 will intercept Habitat-Ω at SS.  Cycler-4 follows Cycler-3 in same manner as Cycler-2 following Cycler-1. Just as first pair of cyclers (Cycler-1 and Cycler-2) start servicing Habitat-α at t=0 days; second pair of cyclers (3 & 4) will start service for Habitat-Ω at t=121.8 days. SUMMARY:  During first year of orbit, Earth controlled Habitats accomplish four distinct rendezvous events.   Next, we consider second year of orbit.
ADD 4 MORE CYCLERS
Synchronize four more cyclers (5, 6, 7, and 8) for second year of orbit as shown.  2nd year cyclers will essentially repeat rendezvous events accomplished by 1st year cyclers (1, 2, 3, 4).  During this 2nd year, note the first four cyclers are bunched up near aphelion, Q. REASON:  Constant time differences (i.e. 81.5 days between cyclers 1 and 2) manifest via different distances throughout the orbit.  Inter-cycler distances are much greater near perihelion, q, and much closer near aphelion, Q.  Table shows that cycler speeds are greatly affected by proximity to Sol. NOTE: DIFFERING INCLINATIONS. Pending material .... Could have all 8 cyclers in one 2 year orbit; however, might prove useful to deploy some or all of them into differning 2 year orbits with diff incline...
Rν = ( ℓ 1 + e × cos(ν) ) Let eccentricity, e = c / a =.608 An orbit's semi-latis rectum, ℓ, is distance from focus (i.e. Sol) to cycler at ν = 90°. Reference ray extends from Sol to q, where ν = 0°.  ℓ plays an essential role in computing length of Radius (R) vector as cycler travels around its orbit. Following equation enables calculation of radius length from shortest (q at ν = 0°) to longest (Q at ν = 180°). See Two Year Table. Vν = √( 2μSol Rν - μSol a ) μSol= 132,712,440,018 km3s−2 Furthermore, Rν plays an essential role in computing cycler velocity.  As cycler travels around its orbit, velocity, Vν,  is at maximum at q; then, decreases until it reaches minimum velocity at Q.	SUMMARY: Synergize Habitats Alpha and Omega with 2 year cycler orbits for enormous benefits.  Requires careful placement of lambda, semi-latis rectum.  Such an orbit can have up to eight distinct cyclers.  CONCLUSION: Since one fully deployed two year orbit can have eight cyclers, adding more fully deployed orbits could quickly increase cycler traffic throughout the Solar System. NOTE: Space tugs could provide even more flexibility.

SLIDESHOW

---

---

---

---

VOLUME 0: ELEVATIONAL
VOLUME I: ASTEROIDAL
VOLUME II: INTERPLANETARY
VOLUME III: INTERSTELLAR

---

---

---

---