ACCELERATE FOR A YEAR.
Does this apply when object's speed increases beyond c, speed of light?
Einstein, says the speed of light, c, is absolute; thus, no object can attain a speed greater than c. So, these two giants of science appear to disagree. (NOTE: In subsequent text, Thought Experiment (TE) shows how they agree within limits.) Einstein also says that all observers measure same value for c regardless of observer's own speed. This also seems to conflict with Newtonian concept of speed differential which leads us to believe that faster observers would observe a slower c than slower observers.
To resolve this paradox, TE suggests the remainder concept, which resembles the complement concept of Probability Theory.
See associated table for tabulated results.
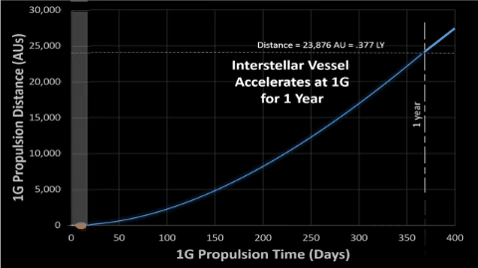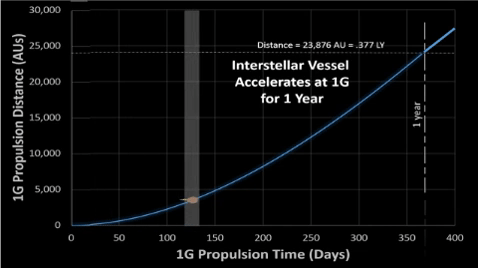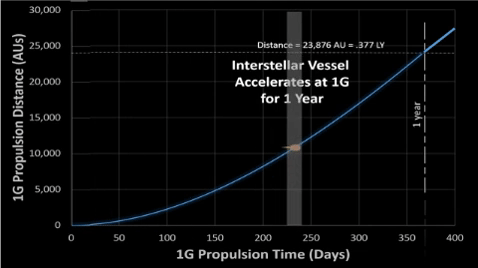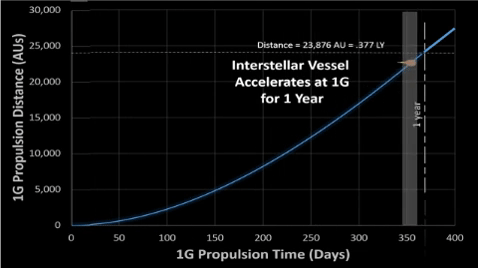 .
.
BACKGROUND:
In the search for practical interstellar travel, Thought Experiment (TE) considers a notional spaceship using a particle accelerator to produce g-force propulsion. The accelerator speeds fuel particles to significant portions of light speed; thus, enormous momentum from a very high speed of a small exhaust mass transfers to a small velocity increase of the spaceship. The propulsion process is designed to produce velocity increase equal to g, acceleration due to Earth surface gravity. Thought experiment further assumes technology advances sufficient to produce a well controlled, consistent flow of exhaust particles at a set speed. Such exhaust particle flows would provide sufficient momentum such that a relatively small mass of fuel could accelerate a larger spaceship at g-force to simulate gravity and gain enormous speeds. Such speeds would require spaceship to g-force decelerate for same duration as acceleration.
QUESTION: How does Probability Theory's
TE proposes the "remainder" concept, an analog of the complement. COMPLEMENT: For any spin of the Roulette Wheel (1st spin, 2nd spin, 100th spin, etc.), the odds of spinning 00 does not deviate from 2.6% and the complement (i.e. "odds of not spinning 00") is always 97.4%. Intuitively, one might wrongly think the odds of ~00 somehow decreases with multiple spins"Complement" Concept relate to interstellar g-force velocities???? LIGHT SPEED REMAINDER ANALOG: For any day of g-force acceleration (1st day, 2nd day, 100th day, etc.), vessel always observes velocity increase of .283%c; remainder (remaining velocity til c, light speed) is always 99.717% c. Intuitively, one might wrongly conclude that remainder velocity decreases after multiple days of g-force, but Einstein says "No" and has been proven to be correct. | To illustrate Probability's "Complement" concept, consider an American roulette wheel which has:
P(00 ¦ 1 spin) = 1/38 = .026

COMPLEMENT: If the event of interest is spinning a 00; then, the event's complement is spinning any other slot (i.e., not spinning a 00).
To compute the probability of NOT rolling a double zero on first roll, use the complement concept as shown:
P(~00¦1 spin)=37/38=.974=1 - P(00¦1 spin)
| |||||||||||||||||||||||||||||||||||||||||||||||
|
P(x) is the probability of event x occurring; P(~x) is the probability of x not occurring (complement of x):
P(~x) = 1 – P(x)
EXAMPLE: Use the complement's probability to determine probability of rolling at least one double zero (00) in three rolls of the wheel? First, determine the probability of a double zero on the first roll. This is easily calculated by dividing number of possible occurrences by total number of possible events.
P(00 ¦ 1 spin) = 1/38 = .026
Next, use the complement to determine probability of NOT rolling a double zero on first roll: Use that value to determine probability of NOT rolling 00 during three successive rolls: Finally, use the complement once again to determine likelihood of at least one double zero during three rolls of the American roulette wheel. What about 10 or any number (n) of spins?? What are the chances of getting at least one double zero??? P(00 ¦ n spins) = 1 - P(~00 ¦ 1 spin)n |
| |||||||||||||||||||||||||||||||||||||||||||||||
Daily Increase in Velocity. After first day of g-force acceleration, velocity can be determined as follows:
Δ = .00283 c = .283% c
|
With exponentials, the complement concept turns a very difficult probability calculation into a very simple one. Note following points:
| |||||||||||||||||||||||||||||||||||||||||||||||

For interplanetary destinations, g-force velocities closely approximate linear Newtonian values. | ||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 | Ship departs Earth and accelerates at g-force. After precisely one day of g-force flight, ship ejects Module-1 with observer. Since Module-1 has no propulsion system, it will maintain constant speed, v1, while g-force ship will continue increasing speed. Earth bound observer measures c at 299,792,458 m/sec and measures Module One's velocity at .283%c. NOTE: Remaining velocity till light speed ("Remainder") is 99.717%c. | |||||||||||||||||||||||||||||||||||||||||||||||
Second Day Scenario: After precisely two days of g-force flight, ship ejects Module Two (M2) with another observer.
M1 observes M2 at .283%c; thus, a remainder of 99.717%c. Earth observes M2 at .566%c; thus, a remainder of 99.434%c.
However, all observers measure same value for c, regardless of platform velocity. (Recall Einstein)
In fact, all observers (Earth, M1, M2, g-force ship) are at different speeds; yet, they all observe c at same value: 299,792,458 m/sec.
|  | |||||||||||||||||||||||||||||||||||||||||||||||
 |
This is true during start, middle or end of flight. However, Earth bound observer will measure different velocities for different modules. First few modules appear to increase speed at a linear rate. | |||||||||||||||||||||||||||||||||||||||||||||||
G-force velocities approximate
a linear relationship for short durations, but this linearity cannot be sustained. How can we resolve this paradox?? | PROBLEM!!! Linear model predicts g-force vehicle will exceed c. Einstein says this can't happen. Most scientists agree; thus, TE considers another way to compute g-force velocities. | |||||||||||||||||||||||||||||||||||||||||||||||
Daily Difference (Δ)
| Remainder (R)
| |||||||||||||||||||||||||||||||||||||||||||||||
Exponentials.
| Daily Speeds.
| |||||||||||||||||||||||||||||||||||||||||||||||
|
First few days of g-force
demonstrate approximate agreement
between Newtonian and Einsteinian models.
| |||||||||||||||||||||||||||||||||||||||||||||||
 |
Day 200 Scenario.
Our notional g-force vessel keeps ejecting modules at precise daily intervals. After 199 and 200 days,vessel ejects modules M-199 and M-200 respectively.Like all the previously ejected modules, M-199 observes velocity of the next module, M-200, at .283%c with 99.717%c remaining until light speed. | |||||||||||||||||||||||||||||||||||||||||||||||
The earth bound monitor observes all 200 modules.
Subsequent modules attain faster velocities
as they eject throughout the voyage.
|  | |||||||||||||||||||||||||||||||||||||||||||||||
|
For greater durations,
values diverge even more between
the models of Newton and Einstein.
| |||||||||||||||||||||||||||||||||||||||||||||||
 |
Eventually, Newtonian velocity (V) exceeds c.
After 354 days, V exceeds 100% c, an impossible feat.
Thought Experiment assumes Einsteinian method
better determines g-force velocities
(especially for long durations). | |||||||||||||||||||||||||||||||||||||||||||||||
SUMMARY | ||||||||||||||||||||||||||||||||||||||||||||||||
Newtonian Method
closely approximates velocities for first few days of g-force flight.
Δ (Daily Difference of g-force velocity) remains a constant 0.489 AU/day ≈ 0.283% c. For convenience, thought experiment assumes following formula:
.489 AU/day × tDay = VFin = Δ × tDay = .283%c × tDay
works well for short interplanetary flights. Thus, 10 day interplanetary trip would reach velocity of 4.89 AU/day ≈ 3% c, well short of light speed. Relativity concerns prevent this linear increase to go on indefinitely, but it's a fairly good model for interplanetary travel with g-force propulsion systems. For much longer interstellar voyages, this formula will need adjustment to produce usable values.
Newtonian values don't prove true for much greater durations. (Example: After 354 days of g-force, above formula predicts velocity exceeds c, an impossibility.)
|
Einsteinian Method
more closely approximates g-force speeds for interstellar flights.
Thus, TE assumes following equation:
Vt = c - c(1 - Δ)t
G-force interstellar flight durations take years (much longer than the few days required for interplanetary flights). The distances are too vast and the flight durations are too great; thus, we cannot get by with the convenient heuristic used for Volume 2, Interplanetary.
Following cells demonstrate how we can
leverage a simple probability concept to derive above equation. | |||||||||||||||||||||||||||||||||||||||||||||||
 Spin the Wheel |  G-force to the Stars. G-force to the Stars. | |||||||||||||||||||||||||||||||||||||||||||||||
| Probability of rolling a double zero on first roll is very low. | G-force velocity after first day of flight is very low, a small percentage of c. | |||||||||||||||||||||||||||||||||||||||||||||||
| P (00) = 1/38 = .026 = 2.6% | V (1 day g-force) = 847 km/sec ÷ 299,792 km/sec = .283% c = V1dy | |||||||||||||||||||||||||||||||||||||||||||||||
| Complement(00): P (~00) =1 - P(00) = 97.4% = C1Spin | Remainder: c - V1dy = 99.717% = R1dy | |||||||||||||||||||||||||||||||||||||||||||||||
| If one knows the probability of an event's complement; then, easily determine the probability of the event:
P(E) = 1 - P(C)
| If one knows the remainder of an g-force vessel's velocity; then, one knows the velocity of the vessel:
Vt = c - Rt
| |||||||||||||||||||||||||||||||||||||||||||||||
 Spin 38 Roulette Wheels Spin 38 Roulette WheelsIntuitively, it seems that at least one must show double zero. NOT SO!!!! |  After accelerating for one year (365.25 days of g-force), After accelerating for one year (365.25 days of g-force), Newtonian physics leads one to believe that velocity will exceed c, light speed. NOT SO!!! | |||||||||||||||||||||||||||||||||||||||||||||||
| After the first few spins of the wheel, it looks like the probabilities are additive. But after many spins, this proves to not be true. | After the first few days of g-force, the resultant velocities appear to add. However, Einsteinian Relativity demonstrate that g-force velocities cannot continue to add indefinitely. | |||||||||||||||||||||||||||||||||||||||||||||||
| To observe results of 38 spins, one could record each spin in sequence. Alternatively, 38 observers could simultaneously spin 38 separate wheels and record the results. | To observe one year of g-force velocities, an Earth bound observer can measure all 365 daily velocities of a g-force vessel. Alternatively, one could conveniently observe 365 markers with constant velocity achieved at time of ejection. | |||||||||||||||||||||||||||||||||||||||||||||||
| As number of spins increase, complement of double zero decreases; this is easily computed with exponentials.
C(00| n Spins) = .974n= Cn-Spins
| As g-force flight duration increases, decreasing light speed remainder is easily computed with exponentials. EXAMPLE: After 1 year of g-force, Remainder (R) decreases to .99717365.25= .3552.
V1Year = c - R365.25days = c (1 - .99717365.25) = 64.48%c
| |||||||||||||||||||||||||||||||||||||||||||||||
| The complement of the complement gives the probability that at least one double zero will happen during a given quantity (n) of spins. | The remainder of the remainder gives us the velocity of the vessel after a given quantity (t) of days with g-force propulsion. See associated 1G TABLE: Accelerate for 1 Year. | |||||||||||||||||||||||||||||||||||||||||||||||
P(00| n Spins) = 1 - Cn-Spins
|
Vt = c - Rt = c - c(1 - Δ)t
| |||||||||||||||||||||||||||||||||||||||||||||||
| VOLUME 0: ELEVATIONAL |
|---|
| VOLUME I: ASTEROIDAL |
| VOLUME II: INTERPLANETARY |
| VOLUME III: INTERSTELLAR |


0 Comments:
Post a Comment
<< Home