REFERENCE: ω Rolls the Orbit

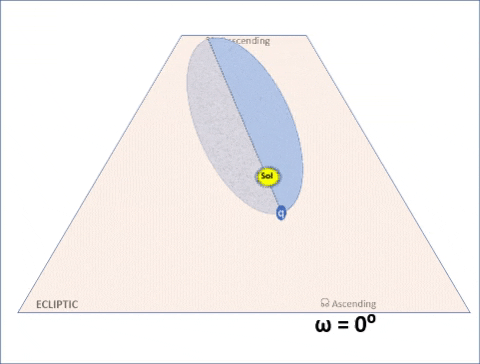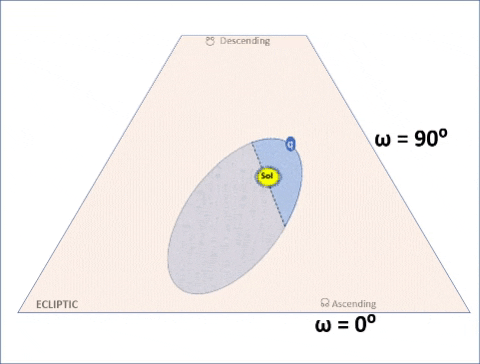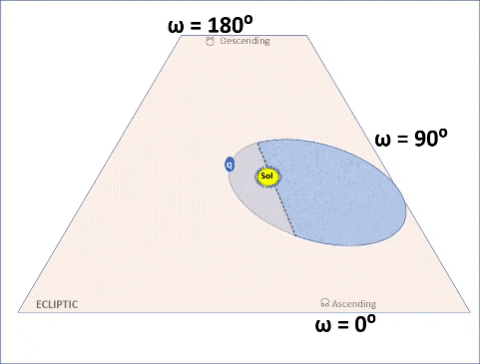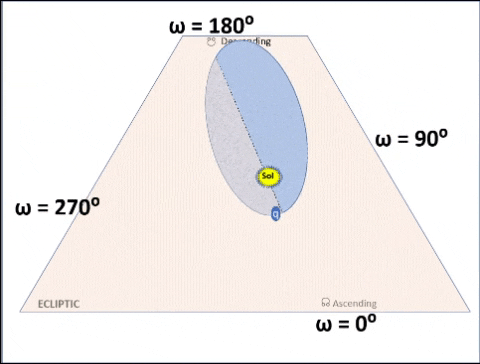Create 36 orbits; all similar except for ω with values increasing  from 0° to 360°.   As ω increases value, the orbit appears to "roll".

OVERVIEW: What is ω?

The argument of perihelion (or arg. of q), designated as ω (Greek lower case “omega”) is one of the six orbital elements. Parametrically, ω is the angle from the orbit’s ascending node (☊) to its perihelion (q) measured in the direction of motion of orbiting object.  Observed from north of Ecliptic, vast majority of asteroids orbit in a Counter Clockwise (CCW) direction. ω is a virtual constant which changes relatively slowly over centuries for many orbits. There are thousands of Near Earth Asteroid (NEA) orbits and each orbit has its own ω with angular value from 0° to 360°.

Typical Asteroid Orbit Pierces Ecliptic.

Asteroid path passes upward (North of Earth) through the Ascending Node (☊). After another 180⁰, it passes downward thru the Descending Node (☋). On the Ecliptic, a notional “Line of Nodes” passes thru Sol between the two nodes.   Argument of Perihelion (ω) is the angle traveled by orbiting object from Ascending Node to Perihelion. EXAMPLE: ω could be 90⁰ as shown.

First Special Case: ω = 000°

OBVIOUS EFFECTS 1) First semi-orbit (θ = 0° to 180°) is above Ecliptic. 2) 2nd (θ = 180° to 360°) is below Ecliptic. 3) Ascension node and descension node coincide with perihelion, q, and aphelion, Q, respectively. 4) Line of Apses coincides with Line of Nodes. NOT SO OBVIOUS. For this special case, let Ω = 0⁰;  then, cos Ω= 1 and sin Ω = 0.  Let ω = 0⁰;   then, ω+Θ = Θ. Finally, let i = 30⁰;   then, cos I = 0.866 and sin i = 0.5.  In this special case, General Transform Equations reduce to: X = R [cos(Θ)] Y = R [sin(Θ) cos(i)] Z = R [sin(Θ) sin(i)]

2nd Special Case: ω = 90°

OBVIOUS STUFF 1) Orbit portion from θ = 270° to 090° is above Ecliptic.   2)  Both semi latus rectum positions (-p and p) coincide exactly with descension and ascension nodes, ☊ and ☋. 3) Sol is exactly in center of Line of Nodes. 4) Perihelion, q, is highest point of orbit. Aphelion, Q, is lowest point. 5) Line of Apses is perpendicular to Line of Nodes. NOT SO OBVIOUS Let Ω = 90⁰; then, cos Ω = 0 and  sin Ω = 1; then, X, Y, Z transformations become: X = R [sin(ω + Θ) cos(i)] Y = R [cos(ω + Θ)] Z = R [sin(ω + Θ) sin(i)] Let ω = 90⁰; then, cos(ω + Θ) = sin(Θ) and  sin(ω + Θ) = cos(Θ). X, Y, Z transformations become: X = R [cos(Θ) cos(i)] Y = R [sin(Θ)] Z = R [cos(Θ) sin(i)]

3rd Special Case: ω = 180°

OBVIOUS STUFF 1) First semi-orbit (θ = 000° to 180°) is below Ecliptic. 2) 2nd (θ = 180° to 360°) is above Ecliptic. 3) Descension node and ascension node coincide with perihelion, q, and aphelion, Q, respectively. 4) Line of Apses coincides with Line of Nodes. NOT SO OBVIOUS Let Ω = 180⁰; then, cos Ω = -1 and sin Ω = 0; then, X, Y, Z transformations become: X = R [-cos(ω + Θ)] Y = R [-sin(ω + Θ) cos i] Z = R [sin(ω + Θ) sin(i)] Let ω = 180⁰; then, cos(ω + Θ) = -cos(Θ) and  sin(ω + Θ) = -sin(Θ). X, Y, Z transformations become: X = R [cos(Θ)] Y = R [sin(Θ) cos i] Z = R [-sin(Θ) sin(i)]

4th Special Case: ω = 270°

OBVIOUS STUFF Resembles special case ω = 90°, but differences include: 1) Highest Z value at aphelion, Q, 2) Lowest is at perihelion, q. NOT SO OBVIOUS Let Ω = 90⁰;  cos Ω= 0 and sin Ω = 1. X = R [-sin(ω+Θ) cos i] Y = R [cos(ω+Θ)] Z = R [sin(ω+Θ) sin i] Let ω = 270⁰;  cos(ω+Θ) = sin(Θ) and sin(ω+Θ) = -cos(Θ). X = R [cos(Θ) cos i] Y = R [sin(Θ)] Z = R [-cos(Θ) sin i]

ACTUAL ASTEROID ORBIT
OBVIOUS STUFF 1) LIne of Apses is not perpendicular to Line of Nodes 2) Sol is not midway between Nodes. General Case Equations. Typical orbit (such as 1862 Apollo asteroid) needs general case equations with more details. Note this includes term for Longitude of Ascension Node, Ω. X = R [cosΩ cos(ω+Θ) - sinΩ sin(ω+Θ) cos i ] Y = R [sinΩ cos(ω+Θ) + cosΩ sin(ω+Θ) cos i ] Z = R [sin(ω+Θ) sin(i)]
SUMMARY
The argument of perihelion (ω) ...  ... is angular distance from Ascension node's (☊) to perihelion (q) for each and every orbit. It is a static parameter for each orbit, but we could observe a virtual ω increasing if we image many notional orbits which are all identical except for ω increasing from 0° to 360°. Observing all these orbits in order of increasing ω, orbit appears to "roll" around Sol. We also notice: 1) Ascension node's (☊) distance from Sol varies Radius (R) from Sol; R ranges from q to Q. 2) As ω increases from 0° to 360°, q rolls around Sol and portion of orbit above Ecliptic varies as shown above. 3) NOT SO OBVIOUS: GENERAL TRANSFORM EQUATIONS can readily convert traditional polar coordinates (R, Θ) for any orbit position into three dimensional Cartesian Coord (X, Y, Z).

SLIDESHOW

VOLUME 0: ELEVATIONAL

VOLUME I: ASTEROIDAL

VOLUME II: INTERPLANETARY

VOLUME III: INTERSTELLAR