SNOWBALL FROM OORT

RESUPPLY MISSIONS. During the several years that interstellar vessels must "cruise" between stars, new resources from the Oort Cloud would be welcome.

Oort Cloud (OC) is a huge, spherical body of comets orbiting Sol from 0.3 light-year (LY) to beyond an entire LY.  It is the most likely source of most long-period comets. For more on Oort Cloud.

As a natural border of Sol's system, Oort Cloud contains "trillions of comets" which could be harvested to benefit humankind.  It is a fair distance from Earth and Sol, human's current environment. At 1 LY (63,241 AU), it will take a typical g-force spaceship profile over two years to travel from Earth. Once there, Sol’s gravity still controls the orbit, even though the extreme distance dims Sol's brightness by many magnitudes.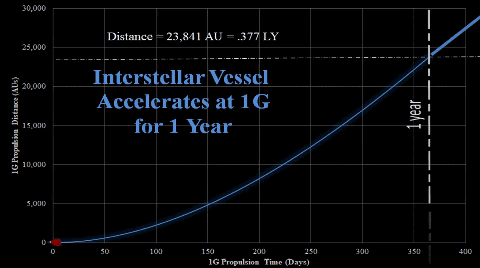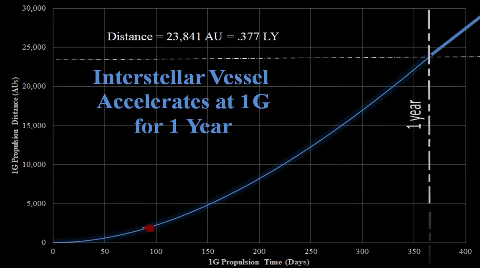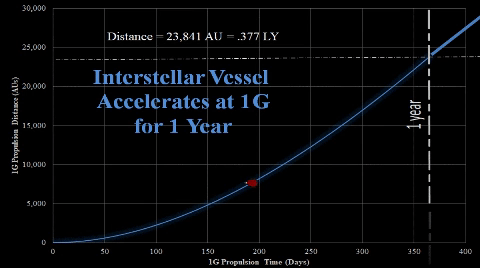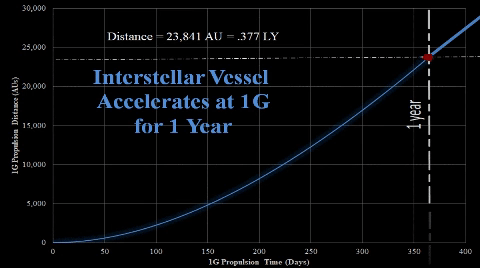

1-G Acceleration Exterior View: Refashioned asteroid Interior View: Mostly empty space to accommodate human habitation. Fuel stored between inner and outer hulls. Acceleration: 1 × g Time (t) Velocity (Vt) Distance (dt) percent c Light Year 365¼ days   64.43%c 0.377 LY Given Vt = c × (1-(1-Δ)t) Einsteinian Velocities dt = c × t + Vt ln(1-Δ ) Einsteinian Distances

7-G Acceleration Assume: Embedded Infrastructure. a. System of robots/nanobots to process heterogeneous mix of water, methane, ammonia, etc. b. Self contained propulsion system can turn of/off as required to eventually match speed of target, the 1G pax vessel. c. Infrastructure Services Include:  Navigation, tracking and communications Assume:  Resupply Vessel Starts Near Sol. While source material comes from far ranging comets, assume they are all dispatched to the Sol area for processing before starting their 100 day acceleration. Acceleration: 7 × g Time (t) Velocity (Vt) Distance (dt) percent c Light Year 100 days 86.44%c 0.155 LY Given Vt = c × (1-(1-Δ)t) Einsteinian Velocities dt = c × t + Vt ln(1-Δ ) Einsteinian Distances

Comets from Sol's Oort Cloud could be refashioned as "snowballs" to resupply interstellar spaceships with many metric Tonnes (mT) of ices. While manned vessels must restrict acceleration to 1-G to simulate Earth gravity for comfort of crew and passengers, unmanned snowballs would not be bound by this requirement. Thus, these resupply vessels could accelerate well past 1g.  For example, 7g acceleration enables a vessel to reach higher speeds and greater distances much quicker than a 1g-force vessel. 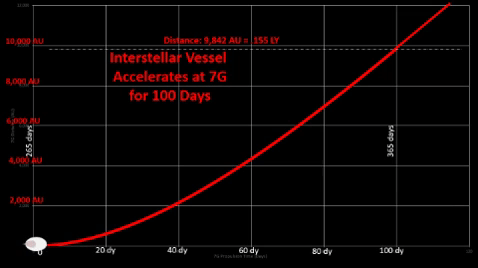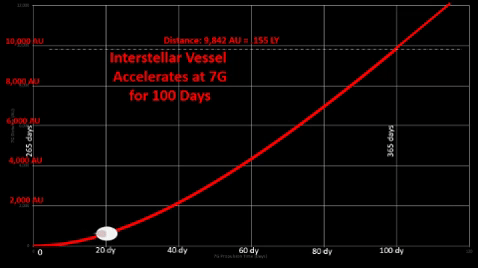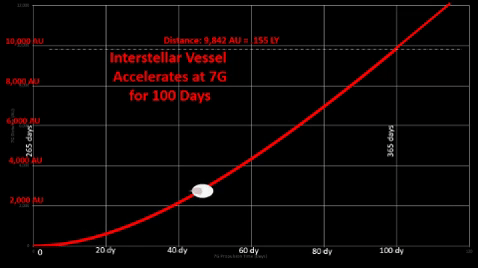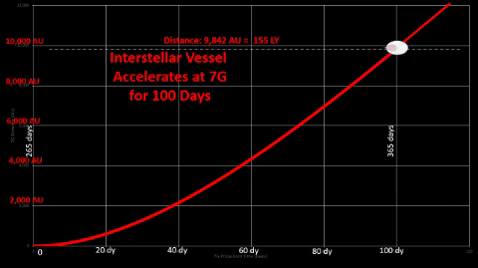Interstellar ships must fly long voyages with sizable populations which could consume considerable resources; thus, Oort Cloud "snowballs" could transport following resources: Fuel from water and other "ices" which can be super heated and ionized into particles. Life support from water and perhaps liquid oxygen. Building materials from "rocky" materials as well as exports from inner Solar System. To derive max benefit from resupply vessels, they should optimize their flight times with minimal waste of energy and quickest flight time.

After 1 year (365 days) of 1-g acceleration, TE's interstellar vessel crew decides to stop propulsion due to fuel concerns. Vessel will maintain constant velocity of 64.4% light speed for several years. Vessel's distance can be described by following equation; d1G = A365  + V1G × t = .377 LY + .644c × t	After 1-g vessel accelerates for 265.25 days, 7-g vessel initiates 100 days of 7-g acceleration. Thus, both vessels start their respective constant velocities around the time the 1-g vessel completes the one year acceleration. 7-g vessel maintains constant .866c for a certain duration. Vessel's distance can be described as follows: d7G = A100 + V7G × t  = .155 LY + .866c × t
	AT CONSTANT VELOCITY, vessels intercept as shown. For first year, both 1-g passenger vessel and the resupply 7-g vessel go through their respective acceleration profiles as described above. Throughout 2nd year, both vessels cruise on the same path to the same destination star at their respective constant velocities.  The 1-g pax vessel is .377 LY (23,841.5 AU) from Sol with velocity of .644 c (= 111.5 AU/day = 193,066 km/sec). The 7-g resupply vessel is much closer to Sol .155 LY (9,802 AU) from Sol with much greater velocity, .866 c (= 149.9 AU/day = 259,620 km/sec); thus, the resupply vessel will inevitably overtake the pax vessel. Compute time of intercept by solving system of linear equations: .377 LY + .644c×t = .155 LY + .866c×t SOLUTION: t  =  1.0 years Unfortunately, there is a huge velocity differential between the two vessels  .866c -.644c = .222c = 38.44 AU/day  = 66,554 km/sec For the two vessels to safely rendezvous, their velocity must be equal at the intercept point; thus, the resupply vessel must decelerate prior.
Deceleration requires following adjustments to Resupply Vessel Profile: LINEAR PROGRAMMING: Start with desired end point; then, work backward to determine required start point.
	7G's Deceleration Endpoint must match 1G vessel's velocity at pre-determined intercept. 7G resupply vessel must decelerate from 149.9 AU to match 1G pax vessel's velocity (111.8 AU/day) exactly at an intercept point. Arbitrarily chose an intercept point of 2.0 years and 64,824 AU after 1G vessel launch. 7G Decel. time Velocity 7G Decel distance 1G Trip Distance 1G Total Trip Time 0  days 149.93 AU/dy 0.0  AU  59,416 AU  682.25 days 1  day  149.46 AU/dy 149.4  AU  59,565  AU 683.25 days ... ... ... ... ... 48 days 112.1 AU/dy 6,444.9 AU 64,796 AU 730.25 days 7G VESSEL MATCHES CRUISE VELOCITY OF 1G VESSEL 48¼ days 111.8 AU/dy 6,472.8 AU 64,824 AU 730.5 days Given (1-Rt) × c dt - dt-1 c × t + Vt ln(R) tA+ tcr + tD Numerical methods help us back off 48¼ days from deceleration endpoint to the deceleration start.  For more details, click: 7G Dec
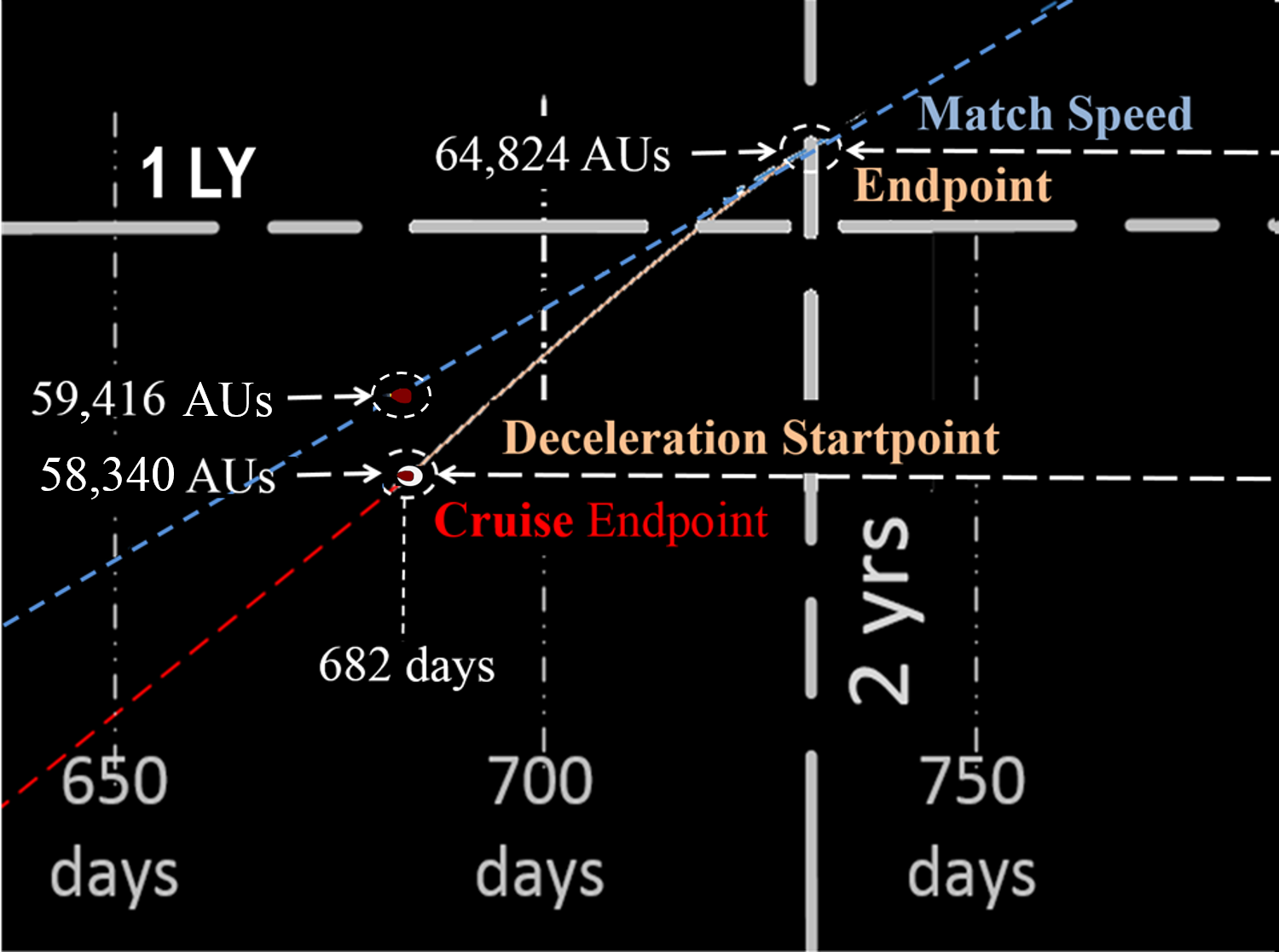
ADJUST ENDPOINTS OF 7G CRUISE ⓐ 360.2 Days: ADJUST 7G CRUISE START.  Change from 365.25 days to 360.2. Cruise velocity of 149.9 AU/day requires 7G acceleration duration of 100 days. Thus, entire 7G acceleration shifts as shown below.  7-g cruise distance has new ordinate intercept (YO): dAU=-44,986AU+tDy×149.9AU/day ⓑ 365.25 Days: 1G VESSEL STARTS CRUISE.  1G vessel stops acceleration; starts 1G cruise; velocity = 111.5 AU/day as described above. ⓒ  400 days: Resupply vessel lags pax vessel by 11,982 AU. ⓓ  500 days: Due to much greater speed, resupply vessel shortens the lag to 8,142 AU. ⓔ  600 days: The lag is further shortened to 4,302 AU. ⓕ  684 days: When resupply vessel reaches 1,076 AU behind the pax vessel, it prepares to decelerate. Cruise segment ends at point where deceleration starts.
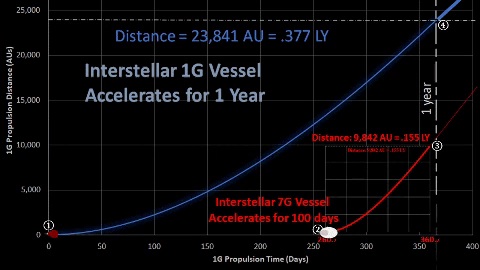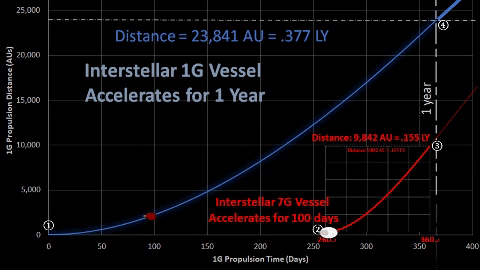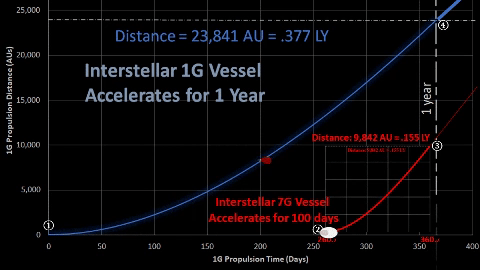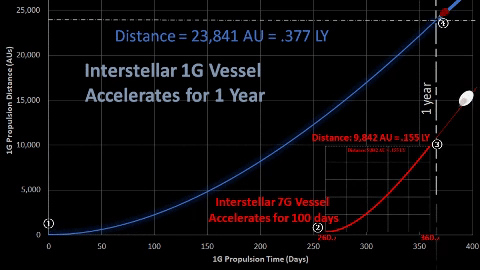	7G VESSEL SHIFTS ACCELERATION ① t = 0.0 days. Initiate acceleration of 1-g vessel for passengers ("pax"). ② t = 260.2 days. 7G resupply vessel launches and accelerates. This 5 day adjustment proves necessary to eventually intercept the pax vessel in two years past point ①. ③ t = 360.2 days.  7-g vessel stops acceleration and starts constant velocity, a linear function. For more details, click: 7G Acc ④ t = 365.25 days.  1-g vessel stops acceleration and starts constant velocity. For more details, click: 1G Acc
PASSENGER (1G) & RESUPPLY (7G) BOTH DECELERATE IN TANDEM Traditional 1G Profile: Passenger (pax) vessel initially accelerates at 1G for one year to attain velocity of 64.43c over a distance of .38 LY.  After a predetermined cruise duration (most likely several years), pax vessel must 1G decelerate for one year just prior to destination. Resupply 1G Profile starts the same as traditional profile.  However, it differs when pax vessel is joined by resupply vessel which partially decelerates from much higher velocity to match pax vessel's cruise speed.  Finally, the pax and resupply vessel decelerate in tandem just prior to destination. For more, click: 1G Dec

COMPARE INTERSTELLAR FUEL CONSUMPTIONS: 1G vs. 7G Accel. a = 1 × g a = 7 × g Daily Diff. ε∇ = .0468% GW ε∇ = .339% GW Daily Rem. (1-ε∇) = 99.9532% GW (1-ε∇) = 99.61% GW Time (t) Velocity (Vt) Distance (dt) Fuel (ft) Velocity (Vt) Distance (dt) Fuel (ft) percent c Light Year percent GW % light speed Light Year %Gross Wt. 1 day 0.28%c 0.000 003 9 LY 0.048% GW 1.98%c 0.000 03LY 0.339% GW 48¼ days 12.8 %c 0.0087LY 2.35%GW 62.0%c 0.0475LY 14.6% GW 100 days 24.65%c 0.035 LY 4.73%GW 86.44%c 0.155LY 28.82%GW 200 days 43.22%c 0.129 LY 9.24%GW Practicality Prevents Powered Progress Beyond 100 Days at 7G. 300 days 57.22%c 0.268 LY 13.54%GW 365¼ days 64.43%c 0.377 LY 16.23 %GW Given Vt = 173.145 AU day × ( 1 - (1-Δ)t ) Einsteinian Velocities dt = 173.145 AU day × t + Vt ln(1-Δ) Einsteinian Distance ft = 1 - (1-ε∇)t Fuel Consumed For much faster cargo delivery, consider 7g acceleration. Assume fuel exhaust particles have velocity, VExh = 99.2%c, with a corresponding growth factor, n = 7. Thought Experiment proposes Einsteinian motions and exponential fuel consumption. 1G Acc 7G Acc  7G Dec 1G Dec

Flight Phase Passenger Vessel Resupply Cargo Vessel n×G time Incr. Rem Cum. Rem Fuel n×G time Inc. Rem Cum. Rem Fuel Consump. Accel 1×G 365¼days RI=.8377GW RC=.8377GW0 F=.1623GW0  7×G 100 days RI=.7118GW RC=.7118GW0 F=.2882GW0  Cruise RIncr. = (1-.000468)t RCum = P(Ri) R = (1-.00339)t Decel 7×G 48¼days RI=.8540GW RC=.608GW0  F=.392GW0  Cruise RCum = P(Ri) Decel 1×G 365¼days RI=.8377GW RC=.7017GW0 F=.2983GW0  1×G 365¼days RI=.8377GW RC=.5092GW0 F=.491GW0   7G Total Fuel Consumption is 49.1% of vessel's initial Gross Weight (GW0) after following power profile: 1) 100 days 7G acceleration to high speed cruise. 2) 48¼ days 7G deceleration to rendezvous with 1G Pax vessel. 3) 365¼ days 1G deceleration in tandem with Pax vessel to orbit at destination. For more, see More Snowballs.

SUMMARY
PHASE I: ACCELERATION
Refashioned asteroid with G-force propulsion capability Pax vessel accelerates at 1G for one year (365.25 days) Launch Pax vessel at Day Zero (D-0) from Earth to attain velocity of 111.5 AU/dy at a distance of 23,811 AU from Sol, our Sun. Alternatively, this could be stated in equivalent terms as a velocity of .644c (light speed) and .377 Light Year (LY).	Artificial Intelligence (AI)  vessel encased in ice likely harvested from comets. Snowball accelerates at 7G for 100 days. Assume Oort comets are towed to Earth vicinity; then, processed into "snowballs" and launched from there at D-265.25.  At 7G acceleration for 100 days, snowball attains velocity of  149.9 AU/dy (.866c) and distance of 9,802 AU (.155 LY).
PHASE II: CRUISE AT CONSTANT VELOCITY
Pas vessel spins during Cruise Phase to simulate Earth like gravity. Pax vessel cruises at .644c for another year of Earth time. DILATED TIME: Due to relativistic effects, on board humans observe and live "dilated" time of 0.7650 years during the Earth observed period of 1.0 year. CRUISE AFTER 365.25 DAYS 1-G After 365.25 days after initial launch, Pax vessel ends 1-G propulsion to stop accelerating and conduct its cruise phase for a year (as observed from Earth). c=173.145 AU/day; LY=63,241.1 AU DPax = dAcc + VCru × tYr DPax = 23,811AU+111.5AU/dy×365.25 dy  DPax = 63,241.1 AUs	Artificial Intelligence (AI) vessel needs no simulated gravity. Snowball cruises for a year of Earth time at much faster speed, .866c. DILATED TIME: Due to relativistic effects, on board systems measure "dilated" time of 0.50 years during the Earth observed year. CRUISE AFTER 100 DAYS 7-G At 365.25 days after pax vessel launch, Snowball ends 100 days of 7-G propulsion to stop accelerating and start its own cruise in synchrony with pax vessel. Like Pax vessel, Snowballs cruise continues for a year (as observed from Earth). DSno= dAcc + VCru × tYr DSno = 9,802 AU+149.9 AU/dy×365.25 days DSno = ‭64,552.975‬‬ AU = 1.02 LY
PHASE III: INTERCEPT AND RENDEZVOUS
Observed from Earth, Pax Vessel  and Snowball take about a year to intercept. Intercept Computed  from Distance and Velocity  of Each Vessel. DPax = 23,811AU+111.5AU/dy×t  DSno = 9,802 AU+149.9 AU/dy×t At intercept time, much faster Snowball overtakes Pax vessel to equalize their distance from Sol.  Solve above system of equations for duration, t. DPax = DSno t = 14,009‬ AU  / 38.4 AU/dy = ‭364.81 dy To determine intercept distance, insert "t" value into one of the equations. DPax = 23,811AU + 111.5AU/dy×364.81 dy = ‭64,487.315‬ AU = ‭1.0197 LY As a check, insert same value into other equation. DSno  = 9,802 AU + 149.9 AU/dy×364.81 dy = ‭64,487.019‬‬ AU = 1.0197 LY	AI Snowball must gracefully  rendezvous with Pax vessel. Rendezvous Requires  Slowdown of Snowball  to Match Speed of Pax Vessel. Unfortunately, there is a huge differential (Δ) between the two cruise velocities. Δ = .866c -.644c = .222c  Δ = 38.44 AU/day  = 66,554 km/sec For the two vessels to safely rendezvous, their respective velocities must match at the intercept point; thus, the Snowball must decelerate prior. Numerical methods help us back off 48¼ days from deceleration end point to the deceleration start point.

SLIDESHOW

---

---

---

---

VOLUME 0: ELEVATIONAL
VOLUME I: ASTEROIDAL
VOLUME II: INTERPLANETARY
VOLUME III: INTERSTELLAR

---

---

---

---