Transfer Orbits

If time aplenty is on your hands;

---

then, a simple transfer will do.

---

If you're not in any hurry;

---

then, you don't need any fuel.

---

 

LIST OF TABLES

CONTENTTABLE-1: Likely DestinationsTABLE-2: Typical TO DistancesTABLE-3: Typical TO VelocitiesTABLE-4: Compare Travel Times.TABLE-5: Compare Travel VelocitiesSIDEBAR: Compare Orbits vs. G-ForceTABLE-6: Compute Fuel as %TOGW.TABLE-7: Adjust %TOGW for EfficiencyTABLE-8: Further Adjust for 2-Way Traffic

Mankind currently orbits to other planets.

---

It takes no fuel, but it takes a while.

---

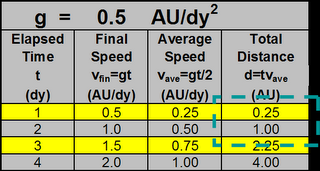
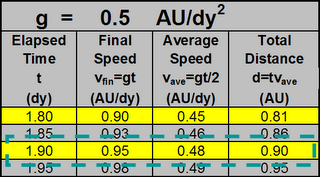
G-force propulsion will be much quicker.

---

It will take some fuel.

Each planetary destination has an observed semimajor axis (a) and period (T).
"a" can be expressed in astronomical units (AUs), meters and kilometers.
AU = 149,597,870,700 m = 149,597,870.7 km
Orbital period, T, can be expressed in seconds and years.
Orbital velocity, v, can be expressed in kilometers per second (kps).
Standard gravitational parameter (μ)
is the product of the gravitational constant and the mass of a relevant dominant astronomical body.
If this body is the Sun, it may also be called the heliocentric gravitational constant (μ_☉).

---

G	=	6.67428 × 1011 m3/(kg-sec2)
M☉	=	1.98892 × 1030 kg
μ☉	=	G × M☉
μ☉	=	6.67428 ×1011 m3 /(kg-sec2)×1.9889 × 1030 kg
μ☉	=	1.32746 × 1020 m3 /sec2 = 39.49 AU3/yr2
√(μ☉)	=	1.15 × 1010 √(m3) /sec = 6.28 √(AU3)/yr

Table 1: Likely Destinations For convenience, Thought Experiment (TE) assumes circular orbits. Semi-Major Axis Period Velocity  a (AU) am (meters) Tsec (sec) T (Yr) VAve  (kps) Earth 1 AU 1.496×1011 m 3.16×107 sec 1.00 yr  29.7 kps Mars 1.52 AU 2.274×1011 m 5.92×107 sec 1.87 yr  24.1 kps Jupiter 5.2 AU 7.779×1011 m 3.75×108 sec 11.86 yr  13.0 kps Saturn 9.51 AU 14.23×1011 m 9.27×108 sec 29.33 yr  9.64 kps Uranus 19.18 AU 28.69×1011 m 26.6108 sec 84.00 yr  6.77 kps Neptune 30.06 AU 47.97×1011 m 52.1×108 sec 164.81 yr  5.78 kps Kuiper Belt 40 AU 59.84×1011m 80.0×108 sec 252.98 yr  4.70 kps Observed a×AUm 2π×√(am3) √(μ) √(a3) 2π×akm Tsec

To determine a typical duration for current technology to travel between planets, Thought Experiment (TE) will briefly consider Transfer Orbits (TOs). Mankind currently uses transfer orbits for their infrequent interplanetary flights. During TOs, space vehicles don't use propulsion for most of the trip.

Thus, TO flights take a long time,

but they don't need much fuel.

---

As a matter of fact, an optimum orbit transfer can get by with only two short engine impulses to shift a spacecraft from one orbit to another.

---

TE focuses on transfers from Earth’s orbit to outer planet orbits.

For convenience, TE assumes all planetary orbits to be circular and co-planar.

---

Typical TO leverages the Sun's gravity to achieve an extremely elliptical orbit with Sol as a focus. TE assumes one fuel burn at the perihelion (closest distance from Sol) to achieve required TO. TE assumes another short burst at aphelion (farthest distance from Sol) to join the destination orbit.

---

While TOs could take several cycles to reach multiple destinations, TE will focus on a typical semi-orbit profile from Earth orbit to destination orbit to determine a typical duration. The Hohmann Transfer is a good model for this

More Info on Transfer Orbits

Select from following. Above information from Universe TodayNASA article about interplanetary trajectories.Davidson University website on orbit transfers.Astronomy Cast, Episode 84: “Getting around the Solar System”Wikipedia: Hohmann Transfer

Hohmann Transfer (HT) is a special case TO; it is considered to be the most fuel efficient. TE uses HT model to conveniently compute some typical TO durations. Furthermore, TE uses some assumptions to further simplify this process. These are discussed later in this chapter.

---

TE settles on HT for "typical transfer times". For more on orbits and on HTs, see book, Orbital Motions, by A. E. Roy.

Table 2: Typical TO Distances

Assume planetary orbits to be circular.

• **Assume ships depart Earth's orbit with radius of 1 AU.
• Semimajor axis, a_D, of destination orbit is observed.
• TO eccentricity [e_TO = (a_D-1)/(a_D+1)] per formula (12.3) on page 355, Orbital Motion by A. E. Roy.
• Transfer Time (t_TO) is half of TO period (√(a³)).
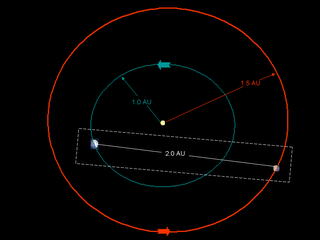
• Transfer Orbit (TO) is the highly elliptical orbit which connects orbit of Earth with orbit of destination planet.
• TO period is the time needed for space vessel to depart orbit of Earth, go to orbit of destination planet; then, return to orbit of Earth.
• Of course, only half this time is needed to transit from Earth orbit to destination orbit (Transfer Time). 
• TO semimajor axis, [a_TO = (a_D+1)/2] is average of Earth's a (1.0 AU) and a_D, destination semimajor axis.
• TO semiminor axis, b_TO , is computed via a common elliptical identity.  
• Transfer distance (d_TO) is approximated by one half of TO elliptical circumference (C_TO ≈ 2 * π * √((a_TO²+b_TO²)/2).)

		T r a n s f e r    O r b i t
Destination	Semi-Major Axis	Eccen- tricity	Semi-Major Axis	Transfer Time	Semi-Minor Axis	Transfer Distance
	aD	eτ	aτ	tτ	bτ	dTO
**Earth	1 AU	D  E  P  A  R  T  U  R  E     O  R  B  I  T
Mars	1.52 AU	0.21	1.26 AU	0.62 Yr	1.23 AU	3.91AU
Jupiter	5.2 AU	0.63	3.10 AU	2.73 Yr	2.41 AU	8.72 AU
Saturn	9.51 AU	0.81	5.26 AU	6.03 Yr	3.08 AU	13.53 AU
Uranus	19.18 AU	0.9	10.09 AU	16.25 Yr	4.40 AU	24.45 AU
Neptune	30.06 AU	0.94	15.53 AU	30.6 Yr	5.30 AU	36.45 AU
Kuiper Belt	40 AU	0.95	20.50 AU	46.4 Yr	6.40 AU	47.71 AU
	Observed	aD-1 aD+1	(1+aD) 2	√(a3) 2	aτ √(1-eτ2)	π√(aτ2 + bτ2) √2

Table 3: Typical TO Velocities

Orbits determine speed, and speed determines orbits;
thus, speed changes determine transfer orbits which change from orbit to orbit.

Transfer Orbit Values are determined as follows:

• TRANSFER DISTANCE (_dτ): From TABLE-2, AUs converted to kilometers. (1 AU = 149,597,870.7 km)
• TRANSFER TIME (_tτ): From TABLE-2, years converted to seconds. (1 yr = 31,557,600 sec = 86,400 sec/day × 365.25 days)
• AVERAGE VELOCITY (_VAve): TE determines average velocity by dividing transfer distance (_dτ) by transfer time (_tτ). Subsequent velocities, minimum (v_min) and maximum (v_max) are determined in a different way.
• Vis-Viva Equation can determine object's orbital velocity at any point in the orbit.
  Transfer Orbit's semimajor axis a_τ is constant for that orbit. 
  Radius vector distance (r_τ) is the Independent variable (IV), and associated velocity v_τ  is the Dependent Variable.

vτ =	√[μ☉(	2 rτ		-	1 aτ	)]

 

Solar standard gravitational parameter (μ_☉) is constant for all objects orbiting Sol(☉), our sun:

μ☉	=	132,712,440,018 km3/sec2

TE decides to modify μ_☉ as follows:

μ☉	=		132,712,440,018 km3 sec2		×	AU 149,597,870.7 km

μ☉	=		887.128 km2 sec2		×	AU

√μ☉	=		29.785 km sec		×	√AU

Thus, Vis-Viva Equation can be modified as follows:

vτ = 29.785 km/sec ×	√[AU(	2 rτ		-	1 aτ	)]

Let r_τ and a_τ be given in AUs; then, AU in radical will cancel out and v_τ can be expressed as:

vτ ≈ 30 kps ×	√[	2 rτ		-	1 aτ	]

Minimum Velocity happens at TO's farthest point from Sun (aphelion, Q_τ).


vτ ≈ 30 kps ×	√[	2 Qτ		-	1 aτ	]

Each TO aphelion is semi-major axis of destination orbit (a_Dest).

Maximum Velocity happens at TO's closest point to Sun (perihelion, q_T).

vτ ≈ 30 kps ×	√[	2 qτ		-	1 aτ	]

Since these TOs use Earth's orbit to depart for outer planets, the aphelion will always be 1 AU, the semimajor axis of Earth's orbit.

vτ ≈ 30 kps ×	√[	2		-	1 aτ	]

CONCLUSION: TO velocity is everchanging due to its highly elliptical shape.  Velocity depends on distance from Sol which changes as object changes orbital position.  Thus, object is at maximum velocity at orbit's perihelion, which happens to be at Earth's orbit (1 AU) as object departs for orbits of outer planets.  Object velocity continually decreases until it reaches orbit's aphelion at orbit of destination planet at which point, object will be at minimum speed.

	Destination	Transfer Orbit
	Semi-Major Axis	Period	Circum	Aphelion	Perihelion	Min Velocity	Ave Velocity	Max Velocity
	aD	P	CT	QT	qT	vmin	vave	vmax
Earth	1 AU	3.16x107 sec	9.40x108 km	1 AU	1 AU	29.81 k/s	29.8 k/s	29.81 k/s
Mars	1.52 AU	4.47x107 sec	1.17x109 km	1.52 AU	1 AU	21.54 k/s	26.24 k/s	32.75 k/s
Jupiter	5.2 AU	1.73x108 sec	2.61x109 km	5.2 AU	1 AU	7.43 k/s	15.15 k/s	38.61 k/s
Saturn	9.51 AU	3.81x108 sec	4.05x109 km	9.51 AU	1 AU	4.22 k/s	10.65 k/s	40.11 k/s
Uranus	19.18 AU	1.01x109 sec	7.32x109 km	19.18 AU	1 AU	2.14 k/s	7.23 k/s	41.11 k/s
Neptune	30.06 AU	1.93x109 sec	1.09x1010 km	30.06 AU	1 AU	1.38 k/s	5.65 k/s	41.48 k/s
Kuiper Belt	40 AU	2.93x109 sec	1.43x1010 km	40 AU	1 AU	1.04 k/s	4.87 k/s	41.65 k/s
	Observed	2π√(aT3) √μ	2π√(aT2+bT2) √2	aT + cT	aT - cT	√[μ( 2 QT - 1 aT )]	CT P	√[μ( 2 qT - 1 aT )]

Consider a typical TO profile:

Semi-orbit. Well planned transfer requires only one half of the first Transfer Orbit. To fly only this semi-orbit, spacecraft changes velocity via carefully planned fuel burns.  An optimal mission would require only the following two burns:

1. First fuel burn enables vessel to depart Earth's orbit and achieve the highly elliptical transfer orbit
2. Second fuel burn occurs when the spacecraft reaches its destination orbit; it changes orbital speed (and hence its orbital shape) to achieve the larger circular orbit.
3. To actually orbit the planet, the spacecraft will have to decelerate again and allow planet's gravity to capture it.

---

 Typical trip time takes years

From start to stop, typical TO speed (see Table 3) takes a long trip to travel the vast distance in one half of the transfer orbit. Typical transfer times can be shown as years (see Table 2).

---

 A long time to endure zero g.

Thus far, we've established that relatively small amounts of thrust at either end of the trip are all that are needed to arrange the transfer. Not much fuel, but even the best planned, luckiest TO ever (where everything goes exactly right, a rare event) will take many months, a long time in lonely space at zero g.

Wait, it gets even worse.

Launch Window. Thus far, TE has only considered the duration of transfers between the orbits of destination planets. For spacecraft to actually arrive at the planet itself, fuel efficiency requires the departure from Earth's orbit to wait until the two planets are properly aligned. Departure time must be planned so the destination planet and the spacecraft will arrive at the same point at the same time. Thus, flight planers must determine a transfer orbit to intersect the destination orbit, and they must also carefully plan the timing of this intersection.

---

TOs between planets via  will be infrequent and fraught with delay

Thus, Transfer Orbit to interplanetary destination is not practical for anything other then infrequent scientific experiments conducted by Artificially Intelligent (AI) devices. Their life support requirements are not as rigorous as humans; they don't need a social life.

Robots can wait.

---

Problems 1 and 2

Above diagram shows a rough sketch of Earth and Mars in their respective orbits around Sol.
Assume planets to be in relative positions shown and that distance between them happens to be 2.0 AU at this time.





Further assume our spaceship is accelerating at rate, g, from Earth to Mars. (Recall g to be acceleration due to force of gravity near surface of Earth, 9.8 m/s/s. For convenience, we're rounding to 10.0 m/s/s.)
Assume velocity at beginning of trip is zero (disregard speed due to orbital manuevers).

Problem: Determine velocity of spaceship at midway, after traveling a distance of 1.0 AU (assume 1 AU = 150,000,000 kilometers = 150,000 megameters).

If we get the same answer by solving this problem in two different ways, that increases our confidence in the solution. Thus, we'll solve this problem in two ways, simple and simpler.

SIMPLE WAY. Build tables. Previous blentries are full of tables; so, following tables will be brief.
Starting at 0 m/s and increasing velocity by 10 m/s, we easily construct following table:

Time _____Velocity
(secs) _____(m/s)
------_____ ---------
__1 _______ 10
__2 _______ 20
__3 _______ 30
__..... ______ ....
__60 _____ 600
==================================
Since 60 secs = 1 min and 1 sec = 1 min/60 (one sixtieth of a min), we can readily convert last entry of above table, and determine that after accelerating for one min at rate, g, our final velocity has reached 600 meters per 1min/60 or 36,000 m/min = 36 km/min.
DETERMINE HOURLY RATE.
Time _____Velocity
(mins) ____(km/min)
------_____ ---------
__1 _______ 36
_10 _______360
_20 ______ 720
_30 ______1080
_..... ______ ....
_60 _____ 2160
==================================
Since 60 mins = 1 hr and 1 min = 1 hr/60 (one sixtieth of an hr), we can readily convert last entry of above table, and determine that after accelerating for one hr at rate, g, our final velocity has reached 2,160 kms per 1hr/60 or 129,600 km/hr = about 130 Megameter (Mm)/hr.
DETERMINE DAILY RATE.
Time _____Velocity
(hrs) ____(Mm/hr)
------_____ ---------
__1 _______ 130
__2 _______ 260
__4 _______ 520
_10 _______ 1300
_20 _______ 2600
_24 _______ 3120
==================================
Since 24 hrs = 1 day and 1 hr = 1 day/24, we can readily convert last entry of above table, and determine that after accelerating for one day at rate, g, our final velocity has reached 3120 Mms per 1day/24 or 74,880 Mm/day = about .5 AU/day.
Since we've determined that accelerating at g will increase our velocity to .5 AU per day after first day's travel, let's take the leap and assume that 10 m/sec**2 = g = .5 AU/day**2. This should be very convenient because interplanetary distances can be easily expressed in AUs.
Time _____Fin Velocity
(days) ____(AU/day)
------_____ ---------
__1 _______ 0.5
__2 _______ 1.0

Since spaceship started at rest and consistently increased speed throughout the trip, we can easily determine average velocity by dividing final velocity by two.
Time _____Fin Velocity_____Ave Velocity
(days) ____(AU/day) ______ (AU/day)
------ ____ --------- ______ ---------
__1 _______ 0.5 __________ 0.25
__2 _______ 1.0 __________ 0.50
__3 _______ 1.5 __________ 0.75
Knowing average velocity, we can apply familiar distance = time * ave-velocity to determine distance traveled.
Time _____Fin Velocity_____Ave Velocity ______ Distance
(days) ____(AU/day) _____ (AU/day) ______ (AU)
------_____ --------- ______ --------- ______ ---------
__1 _______ 0.5 __________ 0.25 ________ .25
__2 _______ 1.0 __________ 0.50 ________ 1.0
__3 _______ 1.5 __________ 0.75 ________ 2.25
__4 _______ 2.0 __________ 1.00 ________ 4.00

Fortunately, distance to midpoint (1.0 AU) happens to fall on our table; thus, we can solve this problem by noting that after traveling 1.0 AUs at acceleration, g (= 10 m/s/s/), we've acheived a final velocity of 1.0 AU per day. However, recall this velocity equals 3,120,000 kms/hour. Since a typical orbital velocity for Early is about 50,000 kms/hour; we have to start SLOWING DOWN in order to orbit around Mars, our destination.

NOTE that above problem solving method was very simple, but time consuming with many opportunities for human error. Next method is simpler but less intuitive. This will be discussed in next blentry, Problem-2.Previous problem (P-1) requested the value for final velocity at midpoint of notional space flight from Earth to Mars. Interesting exercise, but the point is that after constantly increasing velocity at acceleration, g; the midpoint velocity is very high. Thus, we must be able to determine midpoint, because we must SLOW DOWN exactly at midpoint (or adjust some flight parameters, more on that in future blog entries.) Thus, knowing the exact time to start slowing down is even more important then knowing current velocity.
During the solution of problem-1, we needed to determine travel time required to accelerate (at g) to 1.0 AU (150 million kms). Solution used simple equations to build table to determine distances for even increments of travel time (days). Conveniently, 1.0 AU happened to be one of the values in the Distance column.











What if the distance was not on the table? For example, following diagram shows another flight profile with 0.9 AU to the midpoint. Problem-2 requests the travel time to accelerate, g, to 0.9 AU.

Well, the table doesn't have a row corresponding to 0.9 AU, but we can get some utility out of what's there.
--Since 0.9 AU falls between 0.25 and 1.0 AUs, we can interpolate the corresponding travel time between 1 and 2 days of travel time. (NOTE: if the distance value was greater then 4.0 AUs, then we'd have to extrapolate to find corresponding travel time.)





--Since 0.9 is much closer to 1.0 AU then to 0.25 AU, we might speculate the corresponding travel time to be closer to 2 days.

There are many ways to interpolate values from a table. In this problem, let's build another table and adjust the range to focus on the desired values. (We might call this technique, fine tuning.)
















Sure enough, by arbitrarily chosing a range of 1.8 to 1.95 days with .05 increments, we happen to find that traveling at 1.90 days will take us to .9 AUs.

Consider a couple of cosmetic factors.

1. Most people are not now comfortable using decimal days to measure time. Transitioning to a more comfortable utility level can be accomplished in several ways.
Perhaps another table would help.








Thus, we can easily determine that after traveling for one day, 21 hours and 36 mins, we have reached our midpoint of .9 AU, and we should start slowing down. Why? That takes us to our second cosmetic factor.

2. An AU per day appears to be a small, simple quantity, but it is an enormous speed, and 0.95 AU per day is just a little slower. While we could build yet another table, let's just do some simple math.
150 million kms per day = 6.25 million kms per hour
We must reduce this speed to a velocity which will allow our spacecraft to orbit around Mars.

Thanks to Google, we quickly find following linkhttp://filer.case.edu/~sjr16/advanced/mars.html
which tells us that Mars orbital velocity is 24.13 km/sec.
I compute this to 86,868 km/hr which I'll round to 87,000 km per hr.
This equates to a very small fraction of 1 AU per day (24 * 87,000/150,000,000 = 0.014 AU/day). So, I think it's safe to say that the interplanetary navigator can assume 0 AUs per day as the initial speed during departure and furthermore aim for 0 AUs per day for the desired destination speed. Once at the destination, the pilot can take over and fine tune the orbital parameters.

NEO
Near Earth Objects (NEOs) often come within 1 AU of Earth.
A g-force vehicle which travels to these NEOs within days would be a welcome commodity.