REFERENCE: Inclination, the Z factor
Consider the Cartesian X-Y-Z axis where X-Y is the traditional 2 dimensional (2 D) plane, and Z is a factor which adds elevation for a third dimension. (NOTE: This X-Y-Z axis can be rotated and/or inclined for the most effective view of desired orbit. --OR-- Observer can change position to view axis via different perspective.)
 | ||
Observe Asteroid Orbit via Face On View.
Let observer rotate and incline their position to see a complete 2-D view of a chosen asteroid orbit. Thus, observer sees a new X'-Y' axis with no third dimension without Z coordinates (zero Z factor); thus, this view disregards inclination. NOTE: TE chooses X' axis to coincide with asteroid's perihelion or θ = 0°.
| ||
First law of Kepler
Every asteroid orbit is an ellipse with our Sun (Sol) at a focus. Such an ellipse can be modeled by the Radius formula, a polar equation with polar coordinates (R, θ):
| ||
• Independent variable is θ, true anomaly • Dependent variable is R, Radius. Constants: ℓ and e • ℓ is the semi-latus rectum, • e is the eccentricity of the ellipse, Examples: • At θ = 0°, R = q, perihelion, Radius formula reduces to R = ℓ/(1+e) = q. • At θ = 90° and θ = 270°, R = ℓ. • At θ = 180°, R = Q, aphelion, formula reduces to R = ℓ/(1- e) = Q. Finally, convert coordinates from polar (θ, R) to Cartesian (X,Y): • Abscissa: X = R × Cos(θ). • Ordinate: Y = R × Sin(θ). |
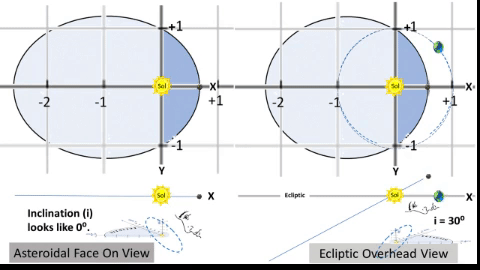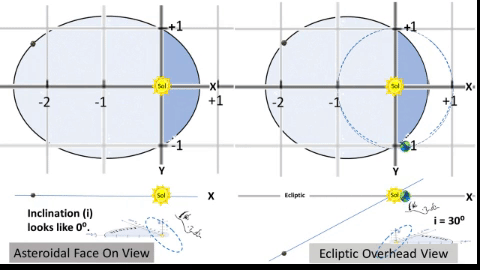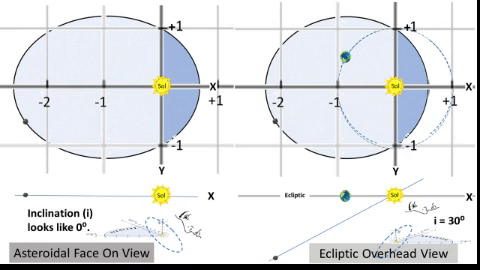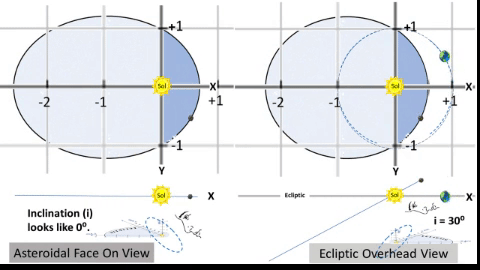
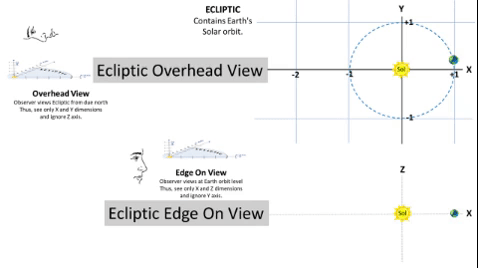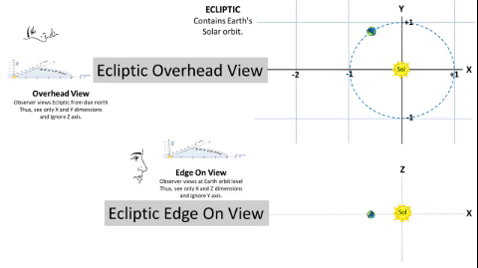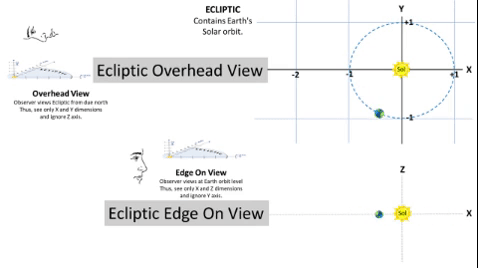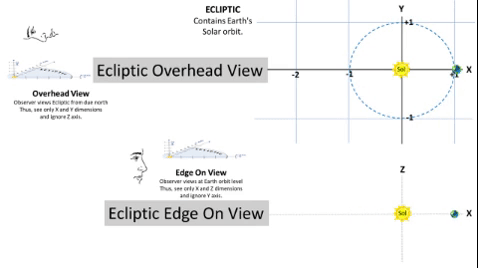
Typical Asteroid Pierces Ecliptic at Two Nodes.
If we consider orbital inclination, we compute a Z-value for all points on the typical asteroid's path to show elevation above/below the Ecliptic plane. At two points, this Z-value will be zero.1) From below the Ecliptic, the asteroid path passes upward (North of Earth) through the Ascending Node (☊), first point where Z = 0. 2) It then travels 180⁰ to travel downward through the Descending Node (☋), 2nd point where Z = 0. 3) On the Ecliptic, there is a notional "Line of Nodes" which connects these two nodes with the Sun between them. This line marks the planar intersection between the Ecliptic plane and the asteroid's orbital plane. 4) Orbital Inclination (i) measures the tilt of an object's orbit. It is the planar angle at the Line of Nodes. |
| Special Case Inclination Depends on Perihelion. Special Case: ω = 90° | ||
| ASSUME: Humankind will someday design an orbit with very convenient parameters. 1) With semi-major axis (a) of 1.58 AU, a populated object (asteroid or hopefully habitat) with a 2 year orbital period (P=730.5 days) could rendezvous with Earth on alternate years. NOTE: Several Apollo type asteroids now have orbital period near 2 years. 2) With perihelion (q, orbit's closest point to Sol) of .622 AU, orbit's semi-latus rectum would be 1.0 AU from Sol to facilitate a good rendezvous point. 3) With argument of perihelion (ω) of 90° (object travels 90° from ascension to perihelion), line of nodes would coincide with the orbit's latus rectum through Sol. Thus, both nodes (ascension and descension) would be exactly 1.0 AU from Sol on the Ecliptic. Thus further facilitates a good rendezvous. 4) When object is at q with true anomaly (θ) of 0°, let Earth lead the object by 48°. Thought Experiment (TE)'s "1st TABLE: 2 YEAR CYCLER at q=0.622 AU" indicates object would rendezvous with Earth about 42.6 days later as it arrives near the node of descension. 5) Let i = 30° inclination (i) for a better graphic demonstration of the Z factor achieved by inclination. NOTE: Most orbital inclinations are much less; however, the asteroid Pallas does have an i = 34° | ||
Variables: θ and R. Same as TABLE 2 (T2). Constants: ℓ and e. Same as T2. Constants: i and ω. • i is orbit's inclination: choose i = 30° to more readily show how i affects Z values. • ω is angular distance from ascending node to q: choose ω = 90°, a special case. Finally, compute 3D coordinates: • X = R × cos(Θ) × cos(i) Example: At θ = 0°, R = q = 0.622 AU; however, X = 0.539 AU, due to projection from the inclined orbit down to the Ecliptic. • Y = R × sin(Θ) Example: At θ = 120°, Y = 1.244 AU, same as for 2D version, see T2. • Z = R × cos(Θ) × sin(i) Example: At θ = 180°, Z = -1.276 AU, lowest Z value of orbit. NOTE: Cross check 3D coordinates. Confirm each 3D orbital point has a Pythagorean result (√(X² + Y² + Z²)) which is same distance as the Radius formula from T2. Example: At θ =240°, R = 1.437 AU = √((-.622 AU)² + (-1.244 AU)² + (-.359 AU)²) = 1.437 AU. | ||
|
| Inclination Depends on Argument of Perihelion. General Case: Any Value ω; EXAMPLE: Let ω = 60° | ||
Variables: θ and R. Same as TABLE 2 (T2). Constants: ℓ and e. Same as T2. Constants: i and ω. • i is orbit's inclination: choose i = 30° to more readily show how i affects Z values. • ω is angular distance from ascending node to q: choose ω = 60°, an example of the general case. Finally, compute 3D coordinates: • X = R × sin(ω+Θ) × cos(i) Example: At θ = 0°, R = q = 0.622 AU; however, X = 0.467 AU, due to projection from the inclined orbit down to the Ecliptic. • Y = R × cos(ω+Θ) Example: At θ = 120°, R= 1.437 AU, but Y = -1.437 AU, due to projection from the inclined orbit down to the Ecliptic. • Z = R × sin(ω+Θ) × sin(i) Example: At θ = 180°, R = 2.553 AU; however, Z = -1.1054 AU, a low Z value but not necessarily the lowest. NOTE: Cross check 3D coordinates. Confirm each 3D orbital point has a Pythagorean result (√(X² + Y² + Z²)) same distance as the Radius formula from previous tables. Example: At θ =240°, R = 1.437 AU = √((-1.078 AU)² + (.718 AU)² + (-.622 AU)²) = 1.437 AU. 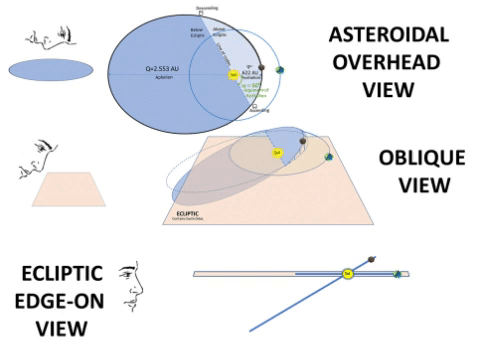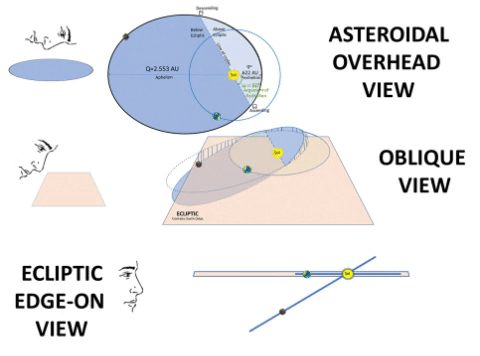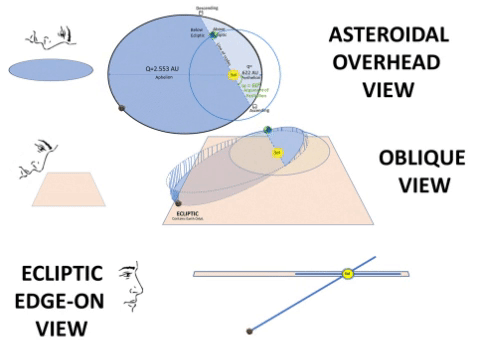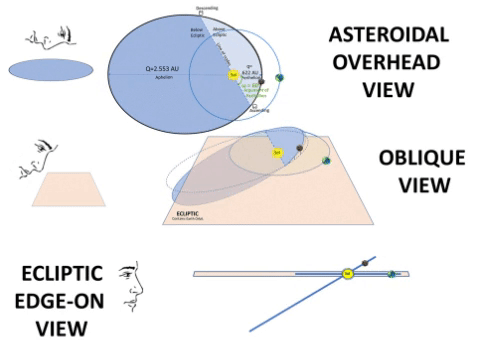 |

0 Comments:
Post a Comment
<< Home