Compute Orbits with Radius Vectors

Determine Elliptic Equation

Given two arbitrary radius vectors from elliptic center, determine equation for elliptic orbit.

For this entirely arbitrary example of two radius vectors from elliptic center to elliptic perimeter, we have calculated values for semimajor axis, a, and semiminor axis, b, to determine elliptic equation.

x2 1.834AU2

+

y2 1.08AU2

=

1

These vectors were limited only by convenience and a few common sense restrictions.

We can use now use values for a and b to calculate:

• focus [c = √(a² - b²) = √(3.65 - 1.08) = 1.6 AU]

• eccentricity [e = c/a = 1.6 / 1.834 = 0.872]

semimajor axis, a > R1 > R2 > b , semiminor axis 0° < θ1 < θ2 < 90° Angle Y=mX X-value Y-value θ Slope (m) r*Cosθ r*Sinθ (Deg) Tanθ Cosθ Sinθ Tan2θ Cos2θ Sin2θ 0° 0 1 0 0 1 0 30° 1/√3 √3 / 2 1/2 1/3 3/4 1/4 45° 1 √2 / 2 √2 / 2 1 1/2 1/2 60° √3 1/2 √3 / 2 3 1/4 3/4 90° ∞ 0 1 ∞ 0 1 0° 0 1 0 0 1 0 26.565° 1 / 2 2/√5 1/√5 1/4 4/5 1/5 45° 1 √2 / 2 √2 / 2 1 1/2 1/2 63.435° 2 1/√5 2/√5 4 1/5 4/5 90° ∞ 0 1 ∞ 0 1 Examples of convenient trigonometric ratios.
x2 a2 + y2 b2 = 1		Ellipse Equation
x2 a2 + m2x2 b2 = 1		Recall we're looking for intersection of line and ellipse. Thus, substitute line equation (y=mx, slope times x) into term containing "y".
x2* b2 + m2x2 * a2 = a2b2
Solve for a -a2 b2 + a2m2x2 = -x2b2 a2 * (-b2 + m2x2) = -x2b2 a2 * (b2 - m2x2) = x2b2	Solve for b -a2 b2 + b2x2 = -m2x2a2 b2 * (-a2 + x2) = -m2x2a2 b2 * (a2 - x2) = m2x2a2
a2 = x2b2 (b2 - m2x2)	b2 = m2x2a2 (a2 - x2)
a = xb √(b2 - m2x2)	b = mxa √(a2 - x2)
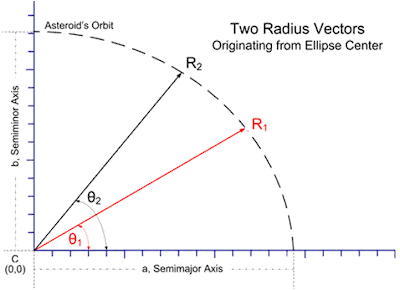
Assume 1st vector, (r1, θ1): a = r1cos(θ1)b √(b2 - tan2(θ1)r12cos2(θ1))	Assume 2nd vector, (r2, θ2): b = tan(θ2)r2cos(θ2)a √(a2 - r22cos2(θ2))	Make following substitutions: m = tan(θ) x = rcos(θ)
a = b * r1 * cos(θ1) √(b2 - r12sin2(θ1))	b = a * r2 * sin(θ2) √(a2 - r22cos2(θ2))	Note following trig identity: tan(θ) = sin(θ) / cos(θ) Therefore, tan(θ) cos(θ) = sin(θ)
a2 = b2 * r12 * cos2(θ1) b2 - r12sin2(θ1)	b2 = a2 * r22 * sin2(θ2) a2 - r22cos2(θ2)	For convenience, use following substitutions: x1 = r1cos(θ1) x12= r12cos2(θ1) y1 = r1sin(θ1) y1 2= r12sin2(θ1) x2 = r2cos(θ2) x22= r22cos2(θ2) y2 = r2sin(θ2) y22= r22sin2(θ2)
b2 * x12 b2 - y12 = a2 = b2 * x22 b2 - y22	a2 * y12 a2 - x12 = b2 = a2 * y22 a2 - x22	Since both radius vectors cross same ellipse, they can be used interchangeably as shown. Transitive identity property allow two outside expressions to equal b2 as well as each other.
x12 b2 - y12 = x22 b2 - y22	y12 a2 - x12 = y22 a2 - x22	Deleting common term from both sides, above equations can be written as shown.
x12(b2 - y22) = x22(b2 - y12) x12b2 - x12y22 = x22b2 - x22y12 x12b2 - x22b2 = x12y22 - x22y12 b2(x12 - x22) = x12y22 - x22y12	y12 (a2 - x22) = y22(a2 - x12) y12a2 - y12x22 = y22a2 - y22x12 y12a2 - y22a2 = y12x22 - y22x12 a2(y12 - y22) = y12x22 - y22x12	Rearrange as shown.
b2 = x12y22 - x22y12 x12 - x22	a2 = y12x22 - y22x12 y12 - y22	FINALLY!!! We've isolated terms a2 and b2. We can now substitute arbitrary values as shown in next row.
b2 = 0.54 AU2AU2 - 0.18AU2AU2 0.333 AU2 b = √1.08 AU2 = 1.039 AU	a2 = (0.18AU2 - 0.54 AU2)AU2 -0.107 AU2 a = √3.65 AU2 = 1.834 AU	Arbitrary Example: Recall restriction r1 = 1.2 AU θ1 = 30° r2 = 1.0 AU θ2=45° Recall substitutions x1 =1.04AU y1=.600AU x2= .707AU y2=.707AU x12=1.08AU2 y12=.36AU2 x22=.5AU2 y22=.5AU2 x12y22 = 0.54 AU2AU2 x22y12= 0.18 AU2AU2 x12 - x22 = 0.333 AU2 y12 - y22= -0.107 AU2

Problem: Can't Count on Convenient Vectors

Previous table used "arbitrary" vectors deliberately chosen for angles with convenient trig ratios

This table assumes that choosing random values from a useable range would be much more realistic of typical observed values.

Thus, this table takes two random radius vectors from an elliptic orbit and determines equation for elliptic orbit.

a > R1 > R2 > b 0° < θ1 < θ2 < 90° Example of two random vectors: r1 = 1.45 AU θ1 = 13.5° r2 = 1.424 AU θ2=21° x1 = r1cosθ1 y1= r1sinθ1 x2= r2cosθ2 y2= r2sinθ2 x1 =1.41AU y1=0.34AU x2= 1.33AU y2=0.51AU x12=1.99AU2 y12= .11AU2 x22=1.77AU2 y22= .26AU2 x12y22 = 0.52 AU2AU2 x22y12= 0.20 AU2AU2 x12 - x22 = 0.22 AU2 y12 - y22= -0.15 AU2 b2 = x12y22 - x22y12 x12 - x22 a2 = x22y12 - x12y22 y12 - y22 b2 = 0.52AU2AU2 - 0.20AU2AU2 0.22 AU2 a2 = 0.20AU2AU2 - 0.52AU2AU2 -0.15AU2 b = √(2.364AU2 - 0.909AU2) a = √[(-1.333+ 3.47)AU2] b = √1.455AU2 a = √2.16 AU2 b = 1.206 AU a = 1.47 AU
x2 a2 + y2 b2 = 1 = x2 (1.47 AU)2 + y2 (1.20 AU)2		Ellipse Equation
√[ a2 - b2 ] = c = √[ (1.47 AU)2 - (1.20 AU)2 ] = 0.86 AU		Determine focus.
Q = a + c = 2.33 AU and q = a - c = 0.61 AU		Determine aphelion, Q, and perihelion, q.
e = (Q - q) / (Q + q) = 1.72/2.94 = 0.58 AU		Determine eccentricity, e.
l = 2qQ/(Q + q) = 2.84/2.94 = .97 AU		Determine semilatus rectum, l.
R(ν) = l 1 + e * Cos(ν)		Familiar Polar Equation for ellipses. Recall the independent variable, ν, is the angle of the radius vector from the relevant focus (Sol, our sun) to the object's position in the orbit. This differs from above angle, θ, angle from orbit's center.

Problem: Orbits Don't Share Common Center

By definition all Solar objects orbit Sol, our sun. Thus, all ecliptic orbits share the Sun as a common focus.

Thus, it makes a lot of sense to analyze R vectors from Sun and not the Ecliptic center, because every orbit's ecliptic centers will vary widely, but the common focus will be very close to same position. Therefore, this table will examine two random positional vectors from Sol.

q < R1 < R2 < l 0° < ν1 < ν2 < 90° For discussion purposes, restrict current considerations to vectors in above ranges. However, following methods should work with vectors from any quadrant in an orbit. Example of two random vectors follow: (data for Apollo orbit from JPL Horizon's web site.) r1 = 0.694 AU ν1 = 36° r2 = 0.847 AU ν2=70° x1 = r1cosν1 x1= 0.561 AU x2= r2cosν2 x2= 0.290 AU R(ν) = l 1 + e * Cos(ν) Polar Equation for Ellipse: Generates vectors from focus. l = R(1 + e * Cos(ν)) Rearrange to solve for l, semilatus rectum. R1(1 + e * Cos(ν1)) = l = R2(1 + e * Cos(ν2)) R1 + R1*e * Cos(ν1)) = l = R2+ R2*e * Cos(ν2)) Since both radius vectors belong to same ellipse, they can be used independently to compute same l value as shown. Transitive identity property allows two outside expressions to equal l as well as each other. R1 + e * x1 = R2+ e * x2 e (x1 - x2) = R2 - R1 Let x1=R1*cos(ν1) Let x2=R2*cos(ν2) Group like terms. e = R2 - R1 x1 - x2 Solve for e, eccentricity. e = 0.565 e = (0.847 - 0.694) AU (0.561 - 0.290) AU Substitute values and determine e. R1 + e * x1 = l = R2+ e * x2 0.694+0.565*0.561=l=0.847+0.565*0.290 1.01 = l = 1.01 Solve for l in both vectors independently.
R(0°) = l 1+e*Cos(0°) = 1.01 AU 1+0.565*1.0 = 0.645 AU = q		By definition, perihelion is determined at ν = 0°.
R(180°) = l 1+e*Cos(180°) = 1.01 AU 1+0.565*(-1.0) = 2.322 AU = Q		By definition, aphelion is determined at ν = 180°.
c = (Q - q) / 2 = (2.322-0.645)AU/2 = 0.8385 AU		Determine focus.
a = Q - c = 2.322 AU - 0.8385 AU = 1.4835 AU		Determine a, semimajor axis.
b = √(a2-c2) = √(1.4835 AU2-0.8385 AU2) = 1.224 AU		Determine b, semiminor axis.

Problem: Observations are from Earth, not Sun. This, Earthly vectors must be translated to Solar vectors. This solution could use special case of midnight observations at zenith from Equator.

Problem, many problems when observing from Earth, atmospheric refraction, diff lat/lon. If we choose to pursue this, we'd need to translate all observations to special case of midnight observations at zenith from Equator.