REFERENCE: ORBITS OF EARTH vs. APOLLO

---

---

---

OVERHEAD VIEW.  If an observer looked directly down from perpendicular vantage point, one would get a full 2D (x-y axis) view of Apollo's asteroidal path.  For convenience, Earth orbit is also shown in same manner; thus, it is circular.

OBLIQUE VIEW gives observer a partial 3D view of all three axii (x-y-z).  Note Earth orbit now appears elliptical.

EDGE-ON VIEW gives observer a 2D view of X axis vs. Z axis, which shows Apollo's inclination compared with Earth's flat path which does not deviate from Ecliptic.

ALL THREE VIEWS show a "hiccup" in Earth's orbit because Apollo's orbital period (about 650 days) is about 80 days short of 2 years (about 730 days).  (NOTE: If Apollo's period was 2 years, it would "resonate" with Earth's orbit, and "hiccup" would dissipate.)

---

---

---

BACKGROUND

1862 Apollo is a near Earth asteroid, approx 1.5 kms in diameter. Discovered by German astronomer Karl Reinmuth at Heidelberg Observatory on 24 April 1932; then, not observed again until 1973. It is the namesake and the first recognized member of the Apollo asteroids, a group of NEAs which seem to cross the orbit of Earth when viewed perpendicular to the ecliptic plane (NOTE: object’s inclination might prevent actual intersection). (See NASA's description of the NEO groups.)

Source material from NASA's orbital diagram generator. Orbit's furthest point from Sun, aphelion (Q) Orbit's nearest point to Sun, perihelion (q) Recall that Q and q are endpoints of the orbit's major axis; thus, Q+q=2a where a = length of semi-major axis. Thus, Orbit's average distance to Sun is semi-major axis, a = (Q + q)/2 RECALL: Semi-major axis, a, includes length to focus, c, plus length to perihelion, q. a= c + q = (Q + q)/2 = Q/2 + q/2  c = Q/2 + q/2 - q = (Q-q)/2  2 c = Q - q Eccentricity Finally, this leads to following equation: e =  c a  =  2 c  2 a  =  Q - q  Q + q Orbital Radius Equation R = ℓ 1 + e × Cos(θ) Above equation can readily compute polar coordinates (θ, R) of orbital path. Radius, R, is the straight line distance from Sol to the orbiting object (Recall Kepler's First  Law, Sol occupies one focus of any Solar orbit).  True anomaly, θ ("theta") is the angular distance from the reference ray (θ=0°), from Sol to q, orbit's perihelion. Constants e (eccentricity) and ℓ (semi-latis rectum) stay static while calculating R values.  Eccentricity (e) is measure of "flatness" of ellipse. Semi-Latis Rectum (ℓ) distance from a focus of the ellipse to the ellipse itself, measured along a line perpendicular to the major axis. (See "First 90° of Apollo's Orbit" below.)

Compare Solar Distances ...

... for first 90° of orbit. This helps determine semi-latus rectum, ℓ, of each orbit. 
(NOTE:  R(90^o) = ℓ, distance of semi-latus rectum.)

R(90o) = ℓ =	ℓ 1 + e × Cos(90°)

First 90° of Earth's Orbit. True Anomaly (θ) Dist fm Sun (R) 0° 1 AU 15° 1 AU 30° 1 AU 45° 1 AU 60° 1 AU 75° 1 AU 90° 1 AU Given q=.983 AU;      Q=1.017 AU R = ℓ 1 + e × Cos(θ) e =  Q - q Q + q = .017 ℓ = 2×Q×q Q + q = 1AU Average Radius of Earth's orbit: R = 149,597,870.7 km = 1 AU.  With a very small eccentricty (e=.017), TE assumes constant radius (R = 1.0 AU).  Thus, assume Earth's semi-latus rectum (ℓ) = 1 AU.

First 90° of Apollo's Orbit. True Anomaly (θ) Dist fm Sun (R) 0° 0.647 AU 15° 0.655 AU 30° 0.680 AU 45° 0.724 AU 60° 0.789 AU 75° 0.882 AU 90° 1.010 AU Given q=.65 AU;     Q=2.295 AU R = ℓ 1 + e × Cos(θ) e =  Q-q Q+q = 0.56 ℓ = 2×Q×q Q + q = 1.01 AU From Sol, Apollo's orbit ranges from .65 AU to 2.23 AU. Reference ray starts at θ =0° and .65 AU. At 90°, the ray perpendicular to Major Axis is ℓ, at 1.01 AU.

Compare 2D Positions

Convert polar coordinates (angle, radius) to the x, y coordinates commonly used for the abscissa and ordinate of the Cartesian coordinate system. Apollo's orbit is definitely eccentric; thus, observe R ranges from perihelion, q=0.647 AU, to aphelion, Q= 2.295 AU.

Apollo's Semi-Orbit. True Anomaly Distance from Sun Cartesian Coordinates ν R-value X-value Y-value 0° 0.647 AU 0.65 AU 0.00 AU 15° 0.655 AU 0.64 AU 0.17 AU 30° 0.680 AU 0.59 AU 0.34 AU 45° 0.724 AU 0.51 AU 0.51 AU 60° 0.789 AU 0.40 AU 0.68 AU 75° 0.882 AU 0.23 AU 0.85 AU 90° 1.010 AU 0.00 AU 1.01 AU 105° 1.181 AU -0.30 AU 1.14 AU 120° 1.403 AU -0.70 AU 1.21 AU 135° 1.672 AU -1.18 AU 1.18 AU 150° 1.961 AU -1.70 AU 0.98 AU 165° 2.200 AU -2.12 AU 0.57 AU 180° 2.295 AU -2.29 AU 0.00 AU Given ℓ 1+e Cos(θ) R×Cos(θ) R×Sin(θ) Recall very basic trig identities: x = R Cos(θ); abscissa value, x, obtained by multiplying radius distance times cosine of true anomaly. y = R Sin(θ); ordinate value, y, obtained by multiplying radius distance times sine of true anomaly.

Earth's Semi-Orbit True Anomaly Distance  from Sun Cartesian Coordinates ν R-value X-value Y-value 0° 1 AU 1.00 AU 0.00 AU 15° 1 AU 0.97 AU 0.26 AU 30° 1 AU 0.87 AU 0.50 AU 45° 1 AU 0.71 AU 0.71 AU 60° 1 AU 0.50 AU 0.87 AU 75° 1 AU 0.26 AU 0.97 AU 90° 1 AU 0.00 AU 1.00 AU 105° 1 AU -0.26 AU 0.97 AU 120° 1 AU -0.50 AU 0.87 AU 135° 1 AU -0.71 AU 0.71 AU 150° 1 AU -0.87 AU 0.50 AU 165° 1 AU -0.97 AU 0.26 AU 180° 1 AU -1.00 AU 0.00 AU Given ℓ 1+eCos(θ) 1.0×Cos(θ) 1.0×Sin(θ) With eccentricty of e = 0.0167,  Earth's orbit is nearly circular; thus, TE assumes radius as a static 1.0 AU.  Therefore,  converting polar to Cartesian coordinates is simply determining components of a unit vector, a simple high school exercise.

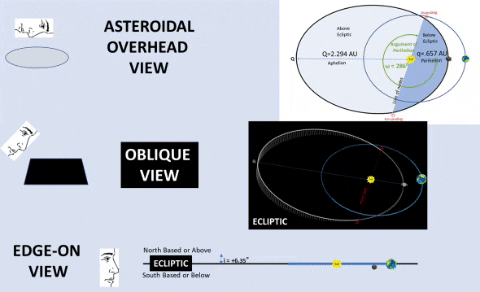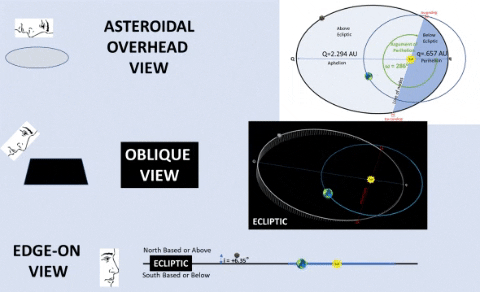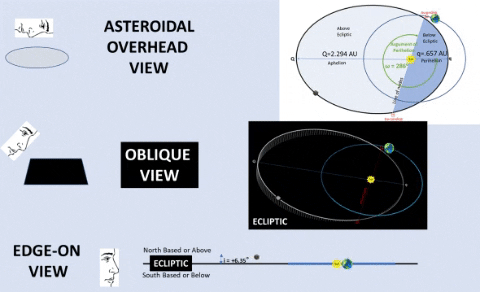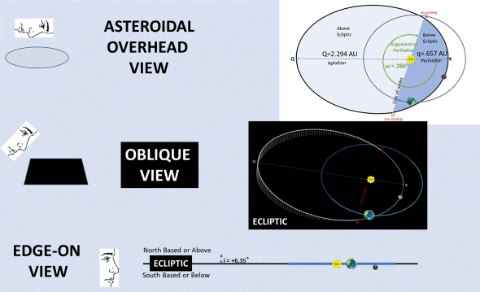
CONSIDER INCLINATION:  Apollo's Orbit Pierces Ecliptic Up and Down.

Compare inclined, elliptical orbit of 1862 Apollo with flat, circular orbit of Earth. NORTH BASED FACE-ON VIEW looks down on Apollo's orbit to observe full range of X-Y values. NOTE: TE arbitrarily chooses X-axis to coincide with the θ = 0° ray from Sol to the orbit's perihelion (q). Furthermore, TE chooses Y-axis to coincide with the θ = 90° ray from Sol to the orbit's semi-latus rectum (ℓ). EDGE-ON VIEW observes asteroid orbit from level of Ecliptic plane. From this vantage point, asteroid orbit looks like a line which passes through the Ecliptic; the line would parallel the Ecliptic plane.

ARGUMENT OF PERIHELION (ω) is an angle from ascending node (☊) to Apollo's perihelion (q, closest point to Sol). This angle is measured in the asteroid's orbital plane and in the direction of motion. By orientating orbit, ω determines which orbital portion is above ecliptic.	LONGITUDE OF ASCENDING NODE (Ω) is an angle, measured Counter Clock-Wise (CCW) from the First Point of Aries (♈︎) to the ascending node (☊).It is measured from 0° to 360° on the Solar Ecliptic. It determines exact date when an orbiting object pierces the ecliptic from below to above.	GENERAL TRANSFORM EQUATIONS. If orbital positions are given as 3D Cartesian (X, Y, Z) coordinates, the Ecliptic contains the X-Y plane and the Z value shows elevation from Ecliptic, Transforming 2D Polar Coordinates (θ, R) of typical Solar orbit into (X, Y, Z) needs detailed equations as shown above.

CONSIDER ORIENTATION:  Apollo's Orbit Slightly Askew.

SIDEBAR: COMPUTE ORBITAL VELOCITIES

Kepler shows how orbital velocity varies per with distance from the Sun. From Kepler and Galileo,  Newton derived the now famous equation: v = √(G × MSol/R) to determine orbital speeds for circular orbits. For Solar orbits, use following values: ●  Universal gravitational constant:         G = 6.67408×10-11 N-m2/kg2 ●  Mass of Sun: MSol = 1.989×1030 kilograms NOTE: Since values G and MSol are constant, their product, G×MSol , is also constant, and it is often expressed as μSol, the Solar System's standard gravitational parameter: μSol = 132,712,440,018 km3 / sec2 = 13.27 x 1019 m3/sec2 Since orbital paths are usually elliptical, use following equation to determine most orbital velocities.   v =  √ ( μ ( 2 R - 1 a ) )

TE Proposes Heuristic Express μSol, the Solar System's standard gravitational parameter in a slightly different way. Instead of meters (or kilometers), input values as Astronomical Units (AUs) for a, semi-major axis, and R, radius from Sol. Thus, adjust value forμSol, as shown below. μSol = 132,712,440,018 km3 / sec2 = 13.27 x 1019 m3/sec2 μSol =    AU × 132,712,440,018 km3 149,597,870.7 km × sec2 = 887.123 AU-km² sec2 Resultant values for orbital velocity at R would be in kilometers per second (kps). Thus, we can more easily determine orbital velocities in km/sec when given orbital values in AUs. To demonstrate this heuristic, compare traditional method versus TE proposed method to compute Apollo's orbit velocity at R = 1.01 AU (=151,093,849,398 m). (Of course, semi-major axis, a, remains a constant 1.47 AU (=219,908,869,916 m) throughout entire Apollo orbit.) COMPARISON:  The traditional method uses large unwieldy numbers. On the other hand, the TE method trades a tiny loss of precision for a whole lot of convenience.

TRADITIONAL CALCULATIONS:  v =√(μ (2/r - 1/a)) v = √(13.27×1019 m3/sec2 × (2/151,093,849,398 m - 1/219,908,869,916 m))  v = √(13.27×1019 m3/sec2 × (1.32368×10-11/m - 0.45473×10-11/m))  v= √(13.27×1019 m3/sec2 × 0.86895×10-11/m) v= √(11.531×108 m2/sec2) Determine square root:  v = 3.396×104 m/sec = 33,960 m/sec Convert to km/sec.  v = 33.96 kps

TE PROPOSED CALCULATIONS:  v =  √ ( 887.123 AU-km² sec2 ( 2 1.01 AU - 1 1.47 AU ) ) v =  √ ( 887.123 AU-km² sec2 × 1.980-0.680 AU ) v =  √ ( 887.123 km² × 1.3 sec2 ) v =  √ ( 1,153.23 km² sec2 ) v =  33.96 km/sec

Compare Orbital Velocities

Compare orbital velocities for similar points on both orbits, Apollo and Earth.  

Apollo's Orbital Velocities Angular Dist. (θ)  Linear Distance from Sun (R) Orbital Velocity(V) deg Astro Units Kilometer km/sec 0° 0.647 AU 96,855,032 km 46.23 kps 45° 0.724 AU 108,234,983 km 43.00 kps 90° 1.010 AU 151,093,849 km 33.96 kps 135° 1.672 AU 250,147,013 km 21.39 kps 180° 2.295 AU 343,395,112 km 13.02 kps Given ℓ 1+e Cos(θ) v =  √ ( μ ( 2 R - 1 a ) )	Terra's Orbital Velocities Angular Dist. (θ)  Linear Distance from Sun (R) Orbital Velocity(V) deg Astro Units Kilometer km/sec 0° 0.983 AU 147,098,074 km 30.29 kps 45° 0.988 AU 147,809,610 km 30.14 kps 90° 1.000 AU 149,556,115 km 29.79 kps 135° 1.012 AU 151,344,387 km 29.44 kps 180° 1.017 AU 152,097,701 km 29.29 kps Given ℓ 1+e Cos(θ) v =  √ ( μ ( 2 R - 1 a ) )

TRAVEL TIMES: Apollo's Range is Wide

TRAVEL TIMES: Earth's Range is Narrow

SUMMARY: Orbit of Earth versus Orbit of Apollo

Eccentricity - Earth orbit is nearly circular (e=.017) while Apollo orbit is highly elliptical (e=.56).

Distances - Earth distances range from closest point, q=.983 AU, to farthest point, Q=1.017 AU. Apollo distances range much more widely from q=.65 AU to Q=2.295 AU.
Orientation - Earth's circular orbit centers on Sol which is much closer to Apollo's perihelion (q) than the aphelion (Q). Also, Apollo's orbital plane is slightly inclined (6.35°) to Ecliptic, plane containing Earth's orbit
Velocities - Apollo's velocities range from 46.94 kilometers per second (kps) to 13.67 kps; by contrast, Earth's range more tightly from 29.30 kps to 30.28 kps.  NOTE: Sidebar's heuristic enables a straight forward calculation of these times.
Sector travel times - Times to traverse 15° sectors vary considerably for Apollo's orbit; sector times range widely from 13.19 days to 45.34 days. By contrast, Earth orbit's sector times closely cluster around 15 days (14.87 days to 15.47 days).  

Ang. Dist.	Sol. Dist.	2D Cart. Coord.		Incr. Dist.	Ave. Vel.	Incr. time	Cum. time	Forecast
θ	R	X	Y	Δ d	V	Δ t	Σ t	Date
Degrees	Astronomical Units				(km/sec)	Earth Days		Gregorian
0°	0.650 AU	0.650 AU	0.00 AU	n/a AU	n/a kps	n/a dy	n/a dy	4/11/2009
15°	0.658 AU	0.636 AU	0.170 AU	0.1709 AU	46.94 kps	13.19 dy	13.19 dy	4/24/2009
30°	0.683 AU	0.591 AU	0.170 AU	0.1767 AU	45.21 kps	13.63 dy	26.82 dy	5/7/2009
45°	0.726 AU	0.513 AU	0.513 AU	0.1889 AU	43.77 kps	14.57 dy	41.39 dy	5/22/2009
60°	0.792 AU	0.396 AU	0.686 AU	0.3333 AU	41.65 kps	16.09 dy	57.48 dy	6/7/2009
75°	0.885 AU	0.229 AU	0.855 AU	0.2376 AU	38.90 kps	18.33 dy	75.81 dy	6/25/2009
90°	1.013 AU	0.000 AU	1.013 AU	0.2783 AU	35.60 kps	21.47 dy	97.29 dy	7/17/2009
105°	1.184 AU	-0.306 AU	1.144 AU	0.3333 AU	31.82 kps	25.71 dy	123.00 dy	8/11/2009
120°	1.406 AU	-0.703 AU	1.217 AU	0.4030 AU	27.71 kps	31.09 dy	154.09 dy	9/12/2009
135°	1.674 AU	-1.184 AU	1.184 AU	0.4823 AU	23.44 kps	37.21 dy	191.30 dy	10/19/2009
150°	1.963 AU	-1.999 AU	0.981 AU	0.5539 AU	19.32 kps	42.73 dy	234.04 dy	12/1/2009
165°	2.200 AU	-2.125 AU	0.569 AU	0.5923 AU	15.81 kps	45.69 dy	279.73 dy	1/15/2010
180°	2.295 AU	-2.295 AU	0.000AU	0.5942 AU	13.67 kps	45.84 dy	325.57 dy	3/2/2010
Given	ℓ 1+e×Cos(θ)	R×Cos(θ)	R×Sin(θ)	√(ΔX2 +ΔY2)	√[μ ( 2 RAve - 1 a )]	Δ d VAve	Σti=Σti-1+Δti **Adjusted	By Inspection.
180°	1.017 AU	-1.017 AU	0.000 AU	0.2653 AU	29.30 kps	15.47 dy	182.625 dy	7/1/2016
195°	1.016 AU	-0.981 AU	-0.263 AU	0.2653 AU	29.30 kps	15.47 dy	198.09 dy	7/17/2016
210°	1.014 AU	-0.878 AU	-0.507 AU	0.2650 AU	29.33 kps	15.45 dy	213.54 dy	8/1/2016
225°	1.012 AU	-0.715 AU	-0.715 AU	0.2645 AU	29.40 kps	15.42 dy	228.96 dy	8/16/2016
240°	1.008 AU	-0.504 AU	-0.873 AU	0.2637 AU	29.49 kps	15.37 dy	244.33 dy	9/1/2016
255°	1.004 AU	-0.260 AU	-0.970 AU	0.2627 AU	29.60 kps	15.31 dy	259.64 dy	9/16/2016
270°	1.000 AU	0.000 AU	-1.000 AU	0.2616 AU	29.73 kps	15.25 dy	274.89 dy	10/1/2016
285°	0.995 AU	0.258 AU	-0.961 AU	0.2605 AU	29.86 kps	15.18 dy	290.08 dy	10/17/2016
300°	0.991 AU	0.496 AU	-0.859 AU	0.2594 AU	29.98 kps	15.12 dy	305.20 dy	11/1/2016
315°	0.988 AU	0.699 AU	-0.699 AU	0.2584 AU	30.09 kps	15.06 dy	310.26 dy	11/16/2016
330°	0.985 AU	0.853 AU	-0.493 AU	0.2576 AU	30.18 kps	15.02 dy	335.28 dy	12/1/2016
345°	0.984 AU	0.950 AU	-0.255 AU	0.2571 AU	30.24 kps	14.98 dy	350.26 dy	12/16/2016
360°	0.983 AU	0.983 AU	-0.000 AU	0.2568 AU	30.28 kps	14.97 dy	365.23 dy	12/31/2016
Degrees	Astronomical Units				(km/sec)	Earth Days		Gregorian
θ	R	X	Y	Δ d	V	Δ t	Σ t	Date
Ang. Dist.	Sol. Dist.	2D Cart. Coord.		Incr. Dist.	Ave. Vel.	Incr. time	Cum. time	Forecast

SLIDESHOW

---

---

---

---

VOLUME O: ELEVATIONAL
VOLUME I: ASTEROIDAL
VOLUME II: INTERPLANETARY
VOLUME III: INTERSTELLAR

---

---

---

---