REMNANTS: VOLUME II, Chap. 6 (Tug to travel)
TERRESTRIAL TUG UPGRADES....
to interplanetary vessel. From shifting between terrestrial orbits among Moon and and satellites, space tugs will grow in size and capability to quickly travel between many planetary systems and many types of habitats such as orbiters, cyclers and even migrators as discussed in VOLUME I: ASTEROIDAL.
| BACKGROUND: Recall Chemical Operations. Current design limitations constrain a chemical fueled rocket to short period "burns". Therefore, one short chemical burst at beginning of flight will speed the vessel to an orbital path to the destination; another short burst at end of voyage slows the vessel to adjust speed with destination orbit. With no additional thrust during the flight, the vessel must stay in a carefully planned Solar orbit for most of the flight. Plasma Performance is Better. Reason for plasma's improved performance, plasma engine constantly propels spacecraft (via plasma ion exhaust) throughout the voyage; this achieves greater speed and does not constrain the vessel to an orbital path.  |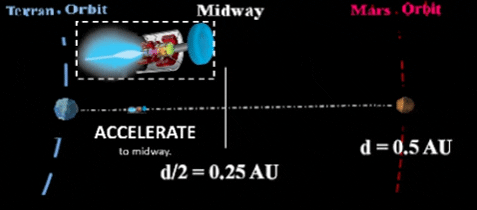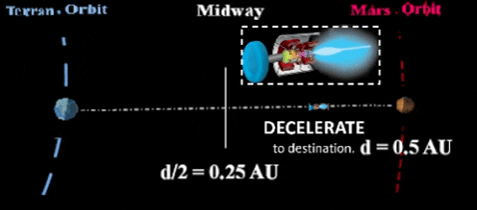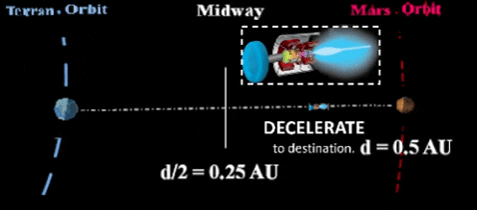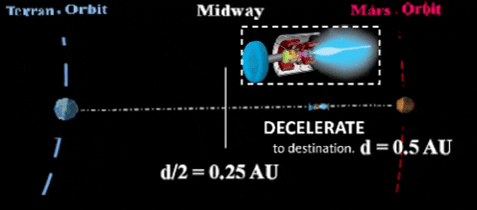
| |||||||||||||||||||||||||||||||||||||||
| HELICON HEATS GASES | ||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Helicon's radio waves heat gases to plasma state (millions of degrees). Thus, rocket performance improves with hotter exhaust; thrust greatly exceeds that of chemical reactants which only reach thousands of degrees in a conventional rocket engine. Thrust from the plasma engine could boost a spacecraft for a longer time and with better efficiency than conventional engines. Plasma engines would have longer and stronger thrust than conventional rocket engines. (Specific impulse.)  SUMMARY: While chemical rockets combine chemical reactants (such as hydrogen and oxygen) for a quick burn, VASIMR exhaust gets much hotter then chemical reactants without burning. It heats a gas until it becomes plasma; the hotter the exhaust, the faster the rocket. | |||||||||||||||||||||||||||||||||||||||
| CHEMICAL ROCKETS ARE SLOWER THAN PLASMA | ||||||||||||||||||||||||||||||||||||||||
Momentum is mass times velocity; in a closed system, momentum exchanges are equal. EXAMPLE: a space borne vessel is a closed system. Left Side Momentum equals Right Side Momentum
| Initially, a traditional chemical rocket will insert the VASIMR vehicle into Earth orbit. Eventually, humans will enter this plasma powered vehicle for travel to interplanetary destinations. BACKGROUND: Traditional chemical rockets are slow. Chemical propulsion uses short duration "burns" to enter/exit transfer orbits. Such orbits are largely constrained by Kepler's laws of orbital motion around the Sun. VASIMR vessels are quicker than chemical rockets. VASIMR's plasma engine stays on throughout the entire trip; thus, velocity constantly increases. In fact, it increases so much that flight profile calls for a "slow down" at mid-way. At exactly mid-way, vessel flips around to propel in opposite direction and start decelerating. Otherwise, the vessel would arrive at destination way too fast for orbital insertion around that planet.  | |||||||||||||||||||||||||||||||||||||||
| VASIMR'S "FLUX TUBE" USES MAG FIELD | ||||||||||||||||||||||||||||||||||||||||
 |
Assume ship size: MShip= 5 mTs = 5×106 gm Assume ship acceleration: a ≈ 5×10-3 m/sec2
Thus, a particle exhaust rate of .025 gram/sec will propel the 5 metric Tonne (mT) vessel 5 millimeters/sec faster for each second of powered flight. .025 gm is a small quantity of mass; how much fuel would be required for constant thrust throughout the 90 day voyage to Mars? First, compute vessel's daily fuel requirement. If a 5 metric Tonne (mT) vessel expends .025 gm of plasma for every second of powered flight, then daily fuel consumption is .00216 metric Tonne.
Fuel requirement for entire voyage can be computed as a percentage of ship's initial gross weight. | |||||||||||||||||||||||||||||||||||||||
For every gram of exhaust fuel flow per sec (ffSec), MShip equals 200 mT.
| VASIMR DIAGRAM BY PIECES  . | |||||||||||||||||||||||||||||||||||||||
| TRADITIONAL PROPULSION TYPES | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Use short burn to leave Earth's orbit, enter a transfer orbit from Earth's orbit to Mars's orbit; then, accomplish a 2nd short burn to enter orbit around Mars. With only chemical reactants, the shortest possible trip would be 6 months in a partial orbit. Most trips call for a much longer duration. Most practical use for chemical reactants would be to move vehicle from Earth's surface to Low Earth Orbit (LEO). Even this dangerous maneuver could be avoided once a space elevator is constructed. | While shorter than 6 months, 3 months is a long time to spend in near 0-g conditions. A more practical use for a plasma drive engine (such as the VASIMR) might be as a plasma injector into a particle accelerator propulsion system. | |||||||||||||||||||||||||
 | ||||||||||||||||||||||||||
3) Particle Accelerator Propulsion (TE'S Brainstorm Technology): Thought Experiment (TE) suggests a third choice. Present day accelerators routinely take ions to near light speeds; thus, TE conservatively assumes exhaust particle velocity of .866c (approaching light speed) which introduces a relativistic growth factor (n) of 2 (particle goes so fast, mass doubles). Considering both this enormous velocity and relativistic growth of exhaust particles, TE uses simple momentum exchange equation to show that particle exhaust flow of .1 gm/sec will propel a 5 mT vehicle about 10 m/sec faster for every second of powered flight. Such acceleration provides g-force to simulate Earth surface gravity (g-force) during powered portions of flight. Furthermore, a trip time to Mars reduces from months to just days, a much more reasonable duration. | T-6: SIMPLE MOMENTUM EXCHANGE shows fuel consumption of .1 gm/sec which grows to particle exhaust flow of .2 gm/sec which propels a 5 mT vehicle 9.8 m/sec faster for every sec of powered flight.
| |||||||||||||||||||||||||
TE notionalizes a possible future of space travel for the human race.
ASTEROIDAL habitats are discussed in Volume I. Over the next century, mankind will become adept of constructing cylindrical habitats from material already in space (mostly asteroids, but comets have their place). Before interstellar flight, humans will gain considerable experience living in large, orbiting habitats which simulate g-force via longitudinal spin. This experience will prove essential for the long, multi-year cruise periods required for interstellar travel.
sdXXXXXXXXXXXXXXXXXXXXXXXXXX
INTERPLANETARYflights will eventually become routine (much like airline travel today) because travel time will decrease to a reasonable duration. Furthermore, spacecraft will maintain comfortable Earthlike conditions (gravity, atmosphere, comfortable billets, entertainment, etc) throughout the flight. Volume II considers Einstein's thought experiment about an accelerating elevator. If the elevator accelerates at same rate as free falling objects near Earth's surface, then occupants will feel same g-force as if they're static on Earth's surface. Instead of Einstein's elevator, our thought experiment notionalizes a high performance spaceship to accelerate at rate, g, to produce gravity like force (g-force). A g-force trip to nearby planets will take days or weeks vs. months or years for constant velocity flights. We speculate this can be done with achievable technology.
INTERSTELLAR flights would take centuries. Even an accelerated flight would take years; Volume III discusses this in detail. Furthermore, fuel would also be a problem. Interplanetary flights can easily carry sufficient fuel to accelerate at constant g-force throughout entire flight (for example, going to Mars would take a few days and a few percent of the ship's mass for fuel); however, interstellar vessels would easily consume well over a 100% of its weight in fuel during the multi-year voyage. Thus, interstellar ships need to separate their voyages into three phases:
INTERSTELLAR flights would take centuries. Even an accelerated flight would take years; Volume III discusses this in detail. Furthermore, fuel would also be a problem. Interplanetary flights can easily carry sufficient fuel to accelerate at constant g-force throughout entire flight (for example, going to Mars would take a few days and a few percent of the ship's mass for fuel); however, interstellar vessels would easily consume well over a 100% of its weight in fuel during the multi-year voyage. Thus, interstellar ships need to separate their voyages into three phases:
- Accelerate to a high percentage of light speed.
- Cruise for a few years at this speed to save fuel (maintain gravity via longitudinal spin).
- Decelerate back to an orbital speed to conduct interplanetary operations at the destination star.
| VOLUME I: ASTEROIDAL |
|---|
| VOLUME II: INTERPLANETARY |
| VOLUME III: INTERSTELLAR |
SUMMARY: In coming days of powered flight, ship's Gross Weight (GW) decreases due to fuel consumption. Subsequently, slightly lighter ship requires slightly less fuel; thus, absolute fuel consumption decreases even though percentage Gross Weight (%GW) remains the same. To model this, TE initially considers a convenient rate of fuel consumption (ffsec=1.0 kg/sec); then, TE determines ship's GW.
However, it's much more likely that flight planners will first determine Take Off Gross Weight (TOGW); then, flight engineers will determine practical fuel flow requirements based on planned TOGW and known efficiency factor (ε).
Define Gross Weight (GW) GW = Structure + Payload + Fuel While structure and payload remain fixed throughout the voyage, fuel decreases throughout powered flight. Assume first day's consumption is .233% of 100,000 mT or 233 mT; then, compute GW for end of day 1: GW1 = GW0 - (GW0×∇Day) = 100,000mT -233 mT = 99,767 mT Second day's fuel consumption could be computed as .233% of first day's GW: F2= ∇Day × GW1 = .00233 × 99,767 mT = 232.46 mT Consider much longer flights. For an indeterminate flight duration, Ft= ∇Day × GWt= ∇Day × (1-∇Day)t× GW0any given day's fuel consumption should use exponents as shown: Example: 40 days. Someday, a g-force trip to Kuiper Belt could require 40 days. Thus, reconsider previous example of 40 days duration with ship size of 100 kiloTonnes. F40= .00233 × (.99767)40×100,000 mT =212.74 mTDecreased daily consumption translates into smaller fuel flow rates. To determine fuel flow for Day 1, divide total fuel consumption by total seconds per day. ffsec = Ft / 86,400 sec = 233×106 gm/86,400sec ffsec = 2,696.8 gm/sec Similarly, Day 2's 232.46 mTs translates into 2,690.5 gm/sec and so on for succeeding days. For the last day (Day 40), we get 2,462.3 gm/sec, a significant 234.5 gm/sec less then the initial flow fuel for Day 1. Thus, to maintain constant g-force throughout powered flight, fuel flow must be constantly monitored and adjusted. G-force sensors (i.e., scales with 100 lbs. weights should indicate 100 lbs. throughout powered flight). Sensor servo connection could automatically adjust fuel flow. | Sidebar: SPECIFIC IMPULSE(Isp)
Specific impulse is measured in seconds. EXAMPLE: one pound of typical solid rocket motor fuel produces one pound of thrust for 250 seconds. Specific Impulse (Isp) is the length of time (usually “seconds”) that each unit weight of propellant propels its own weight. For ships in vacuum of space, it proves convenient to compute specific impulse as average particle exhaust speed divided by g, near Earth gravity:
In contrast, Impulse (I) is the average propulsion Force (F) times the total duration (t) of firing. I = F × t Straight forward work rearranges terms for Impulse equation such that Impulse equals exhaust mass flow times velocity of exhaust particles. F = ma = m × v/t I = F × t = m × v (i.e., momentum) For now, assume perfect efficiency; thus, exhaust fuel flow equals input fuel flow: I = ffExh × VExh Effects of relativity on size of exhaust particles. ffExh = n × ffsec For VASIMIR rocket engine, relativity is negligible and n=1 I = ffsec × vExh Recall ffExh is the amount of exhaust mass per time ejected out of the rocket (adjusted for relativity). Assuming constant exhaust velocity, we get: I = ffExh × vExh where m is the total mass of the propellant. We can divide this equation by the weight of the propellants to define the specific impulse. The word "specific" just means "divided by weight". Thus, Specific Impulse (Isp) shows Impulse from each unit weight of propellant. For example, typical solid rocket motor produces 250 pounds of thrust for every pound of fuel injected into the combustion chamber (per second). Expressed mathematically:
Isp = F / (ṁ × g0) Mathematically, the Isp is a ratio of the thrust produced to the weight flow of the propellants. A quick check of the units for Isp shows that: = (m/sec) / (m/sec2) = sec Why specific impulse?
|
CONCLUSION: G-force vessel must vary daily fuel consumption.
Fortunately, VASIMR's first name is "Variable"; thus, will vary plasma quantity injected into particle accelerator.
LEADING ION DRIVE
A typical ion drive converts gas (i.e., argon, xenon, or hydrogen) into super heated plasma. To expel high speed ions out of exhaust, a magnetic nozzle directs collective ion motion into useful linear momentum. Ions accelerate to perhaps 50 kilometers per second (about .000167 c). While this exhaust velocity far exceeds speeds achieved by exhaust particles from traditional chemical fueled vehicles, it is not nearly enough to produce g-force throughout a trip to neighbor planets.However, an ion thruster might efficiently inject ions into Thought Experiment's (TE's) on board particle accelerator propulsion system. The best ion thruster might be the VASIMR plasma drive, now under development by the Ad Astra Rocket Corp.
ASTRONAUT-SCIENTIST: DR. FRANKLIN CHANG-DIAZ
Dr. Franklin Chang-Diaz leads a team which developed a revolutionary spacecraft propulsion. His company Ad Astra, now builds the Variable Specific Impulse Magneto-plasma Rocket (VASIMR). As a very different type of propulsion system, VASIMR uses plasma to propel spacecraft.Dr. Chang-Diaz explains the plasma drive: “...rocket engine of the future. As plasma is released through an exhaust nozzle, it creates the rocket effect and pushes the engine (in opposite direction). ... a plasma engine is more efficient and faster. In fact, a plasma-driven rocket could push a cargo vehicle from Earth to Mars in ninety days, about twice as fast as solid or liquid (i.e., chemicals) fueled rockets.”
posted by JimODell at 1:09 AM 
posted by JimODell at 12:45 AM
0 Comments:
Post a Comment
<< Home