Terrestrial HTs
Linear Velocity km/sec | Linear Velocity AU/day | Angular Velocity deg/day | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
Table-1
Orbit Descriptions
Radius(R)
Ang. Vel. (ω)
Daily Diff. (Δ)
Time til Dest. (T)
0.98463 AU
1.0098°/day
0.0232°/day
0.9866°/day
0.0000°/day
0.00 yr
1.01671 AU
0.9624°/day
-0.0242°/day
6.78 yr
| Kcon = | √μSol * 86,400 sec/day 149,597,871 km/AU | * | 180° π | = 0.986585 |
|---|
| Kcon √R3 |
|---|
ωTerra ± ωHab| 60° Δ | * | 1 year 365.26dy |
|---|
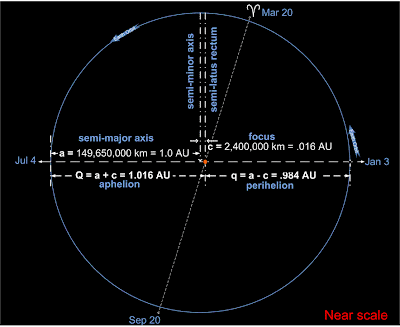
Terrestrial Orbit
Perihelion (q): 152,100,000 km (1.017 AU)
Aphelion (Q): 147,300,000 km (0.985 AU)
Semi-major axis (a): 149,700,000 km (1 AU)
AMPLIFY: Thought experiment now assumes elliptical Earth orbit, e = 0.0154.
e = Q - q
Q + q = 1.017 - 0.985
1.017 + 0.985 = 0.0154
Define terms: Q, q, and e.
For this chapter, thought experiment uses following definitions:
- Aphelion (Q) is orbit’s furthest point from Sol.
- Perihelion (q) is orbit’s closest point from Sol.
- Transfer Orbit. Carefully applied propulsion vectors will transfer an object from one planet's orbit into another.
- Hohman Transfers are the most fuel efficient transfer orbits. For example, propulsion applied to an object at Earth’s aphelion can create a semi-orbit to arrive at Mars during perihelion. Of course, circumstances seldom permit a perfect. The Earth-Mars HT scenario is discussed in next chapter. However, this chapter uses HTs to change terrestrial orbits.
Describe how HT can be used to change orbit's e to zero (0).
If done at Q, orbit's a increases, velocity slows and object lags Terra.
If done at q, orbit's a decreases, velocity increases and object leads Terra.
After sufficient time of Δ v, apply 2nd HT to change orbit back to Earth's e, 0.0154, and maintain lead/lag of 60°.
Earth orbit diagram needs following parameters:
a (semi-major axis) = (Q + q) /2 = 149,700,000 km = 1 AU
c (focus) = (Q - q) /2 = 2,400,000 km = .016 AU
Thus, c is difference between Earth's average radius, a, and Q, aphelion, as well as difference between a and q, perihelion.
b (semi-minor axis) = √(a2 - c2) = 149,680,837 km = 0.99987 AU
Observed Solar diameter = 1,390,000 km = .0093 AU = dS
Observed Terran diameter ≈ 12,700 km = dT
Observed Lunar diameter ≈ 3,700 km = dL
Since c / dS = 1.72; we can see (via diagram) that exact center of Earth's orbit about Sun is slightly outside Sol.
Observed average Lunar radius = 384,000 km = .002565 AU = rL ;
thus, diameter of Luna's orbit around Terra is 2rL = 768,000 km = .00513 AU.Since dS/(2rL) = 1.813; Sol is almost large enough to contain two complete Lunar orbits about the Earth (as shown in diagram).
Finally, we see that c/rL= 6.238; launching Omega at aphelion (or Alpha at perihelion) can give us a lot more leverage then just launching at Full Moon or New Moon (see previous chapter, Landing Omega). Rest of this chapter discusses this further.
Important events during each Terran orbit about Sol:
| Event | Cal. Date | Rel. JD | Rel. Angle |
|---|---|---|---|
| Perihelion (q) | Jan 3 | 0 dy | 0° |
| Aphelion (Q) | Jul 4 | 182.6 dy | 180° |
| Vernal Equinox (Aries) | Mar 20 | 76 dy | 74.9° |
| Autumnal Equinox (Opp Aries) | Sep 20 | 260 dy | 256.3° |
| Summer Solstice | Jun 21 | 169 dy | 166.6° |
| Winter Solstice | Dec 21 | 352 dy | 346.9° |
All Julian dates (JDs) computed for CE 2010 at same daily time of 12:00:00.0 UT (except for Q).
EXAMPLE: JD for Jan 3 is 2455200 and Mar 20's JD is 2455276.; thus, relative Julian Date is diff, or 76 days.
Relative angle estimate based on circular orbit assumption.
Relative angle = 360° *(76/365.25) = 74.9°.
On first glance, the HT method seems the way to go.
16 years is certainly much quicker then 44 years.
It seems much more elegant and productivel then the stable circle method. Surprisingly, the longer method might turn out to be the actual method used. Consider the following.
There could be several problems from using periodic propulsion vectors:
1. Orientation of vehicle might prevent application of desired propulsion vector.
2. Period fuel "kicks" might apply excessive strain to habitat's infrastructure.
3. Logistics of acquiring semiannual fuel loads might prove more difficult then the dubious benefit of shaving off a few years from the wait time until arrival at L point.
On the other hand, while habitat is slowly drifting toward its L point, the "wait" time doesn't have to be spent waiting. Productivity can be ongoing.
1. Habitat population can pursue onboard construction as required.
2. Habitat can still begin main function of receiving "chunks" of material from NEO (comets and asteroids) and can still process them.is simpler and saves considerable fuel. However, it takes much longer then the Hohman Transfer method (44.4 years for stable circle vs. about 16 years for HT method).On first glance, the HT method seems the way to go.16 years is certainly much quicker then 44 years.It seems much more elegant and productive then the stable circle method. Surprisingly, the longer method might turn out to be the actual method used. Consider the following.There could be several problems from using periodic propulsion vectors:1. Orientation of vehicle might prevent application of desired propulsion vector.2. Period fuel "kicks" might apply excessive strain to habitat's infrastructure.3. Logistics of acquiring semiannual fuel loads might prove more difficult then the dubious benefit of shaving off a few years from the wait time until arrival at L point.On the other hand, while habitat is slowly drifting toward its L point, the "wait" time doesn't have to be spent waiting. Productivity can be ongoing.1. Habitat population can pursue onboard construction as required.2. Habitat can still begin main function of receiving "chunks" of material from NEO (comets and asteroids) and can still process them.



0 Comments:
Post a Comment
<< Home