Orbital Adjustment
SOURCE DOCUMENT: Wikipedia: Orbital Maneuver
An orbital maneuver uses onboard propulsion systems to change the orbit of a spacecraft. For spacecraft far from Earth (for example those in orbits around the Sun) an orbital maneuver is called a deep-space maneuver (DSM).[not verified in body]
The rest of the flight, especially in a transfer orbit, is called coasting.


Rocket mass ratios versus final velocity calculated from the rocket equation.
Consider the basic rocket principle: accelerate (apply thrust) by expelling part of its mass with high speed and moving due to the conservation of momentum. The Tsiolkovsky rocket equation, or ideal rocket equation relates the delta-v (change of speed of the rocket) with the effective exhaust velocity and the initial and final mass of a rocket (or other reaction engine.).See Wiki article: Tsiolkovsky rocket equation
Consider the basic rocket principle: accelerate (apply thrust) by expelling part of its mass with high speed and moving due to the conservation of momentum. The Tsiolkovsky rocket equation, or ideal rocket equation relates the delta-v (change of speed of the rocket) with the effective exhaust velocity and the initial and final mass of a rocket (or other reaction engine.).See Wiki article: Tsiolkovsky rocket equation
For any such maneuver (or journey involving a number of such maneuvers):
where:
 is the initial total mass, including propellant,
is the initial total mass, including propellant, is the final total mass,
is the final total mass,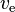 is the effective exhaust velocity (
is the effective exhaust velocity ( where
where 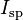 is the specific impulse expressed as a time period and
is the specific impulse expressed as a time period and 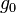 is the gravitational constant),
is the gravitational constant),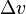 is delta-v - the maximum change of speed of the vehicle (with no external forces acting).
is delta-v - the maximum change of speed of the vehicle (with no external forces acting).
Main article: Delta-v
Main article: delta-v budget
For entire mission, the delta-v budget sums individual delta-v's for each maneuver; thus, engineers can accurately estimate total delta-v for entire mission. A good approximation of the delta-v budget enables flight planners to determine payload requirements which includes spacecraft fuel for inflight maneuvers.
"Impulsive maneuver" mathematically models an instantaneous change in the spacecraft's velocity (magnitude and/or direction) (see Fig. 1). After real burn, any velocity off-set from the theoretical impulsive maneuver is due to the difference in gravitational force along the two paths (red and black in figure 1) usually very small.
Space mission planners will approximate their intended orbital changes via impulsive maneuvers to simplify orbital transition models.
Low thrust over a short duration is a non-impulsive maneuver (see also: finite burn) where "short duration" indicates a relatively small portion of entire mission. However, a short duration is much longer than "instantaneous" burn mentioned above. It refers to the maneuver not being of a short time period rather than not involving impulse- change in momentum).
A space rendezvous would definitely require high fidelity model of the trajectories are required to meet the mission goals. Calculating a "finite" burn requires a detailed model of the spacecraft and its thrusters. Important factors include:
- mass
- center of mass
- moment of inertia
- propulsion systems
- thrust vectors
- specific impulse
- thrust centroid offsets
- fuel consumption
See wiki article: Oberth effect
In astronautics, the Oberth effect describes high speed effects of a rocket engine; high speed rocket generates more energy than at low speed. This occurs because the propellant's kinetic energy can generate more mechanical power. This effect was first described by Hermann Oberth, the Austro-Hungarian physicist and a founder of modern rocketry.
An Oberth maneuver (i.e., "powered flyby") applies a rocket engine impulse near a gravitational body. This produces greater kinetic energy and final speed (i.e. higher specific energy) than the same impulse applied further from the body. For the most effective Oberth effect, the vehicle must generate as much impulse as possible at the lowest possible altitude; thus the Oberth effect is often far less useful for low-thrust reaction engines (i.e., ion drives) with a low propellant flow rate.
Being unaware of the Oberth effect, early investigators concluded that interplanetary travel required completely impractical amounts of propellant.
Main article: Gravity assist
In orbital mechanics, a gravity assist maneuver uses the relative movement and gravity of a planet to accelerate, decelerate and/or re-direct the path of a spacecraft. Typically, this saves the mission: propellant, time, and expense. The "assist" is provided by the motion (orbital angular momentum) of the gravitating body as it pulls on the spacecraft. The technique was used by interplanetary probes from Mariner 10 onwards, including the two Voyager probes' notable fly-bys of Jupiter and Saturn.
Orbit insertion is a transfer orbit or an ascent orbit into a stable one as well as to change a stable orbit into a descent: descent orbit insertion. Also the term orbit injection is used, especially for changing a stable orbit into a transfer orbit, e.g. trans-lunar injection (TLI), trans-Mars injection (TMI) and trans-Earth injection (TEI).
Main article: Hohmann transfer orbit
In orbital mechanics, the Hohmann transfer orbit is an elliptical orbit to transfer between two circular orbits of different altitudes, in the same plane.
The Hohmann transfer uses two engine impulses to move a spacecraft onto and off the transfer orbit. Named after Walter Hohmann, the German
scientist who published a description of it in his 1925 book Die Erreichbarkeit der Himmelskörper (
The A
ccessibility of Celestial Bodies). Hohmann was influenced in part by the German science fiction author Kurd Laßwitz
and his 1897 book
Two Planets
scientist who published a description of it in his 1925 book Die Erreichbarkeit der Himmelskörper (
The A
ccessibility of Celestial Bodies). Hohmann was influenced in part by the German science fiction author Kurd Laßwitz
and his 1897 book
Two Planets
Main article: Bi-elliptic transfer
The bi-elliptic transfer moves a spacecraft between orbits; sometimes, it requires even less delta-v than a Hohmann transfer maneuver.
- The bi-elliptic transfer consists of two half elliptic orbits. From the initial orbit, apply a delta-v to boost the spacecraft into the first transfer orbit.
- Finally, apply a third delta-v to inject the spacecraft into the desired orbit.
Main article: low energy transfer
A low energy trajectory allows spacecraft to change orbits using very little fuel.These routes work in the Earth-Moon system and also in other systems, such as between the satellites of Jupiter. The drawback of such trajectories is that they take much longer to complete than higher energy (more fuel) transfers such as Hohmann transfer orbits.
These are also known as weak stability boundary trajectories, or ballistic capture trajectories.
They follow special pathways in space, sometimes referred to as the Interplanetary Transport Network. Following these pathways allows for long distances to be traversed for little expenditure of delta-v.
Main article: orbital inclination change
Orbital inclination change changes the inclination of an orbiting body's orbit. This is also known as an orbital plane change as the plane of the orbit is tipped. It changes the orbital velocity vector (delta v) at the orbital nodes (i.e. the point where the initial and desired orbits intersect, the line of orbital nodes is defined by the intersection of the two orbital planes).
In general, inclination changes require a great deal of delta-v, and most mission planners try to avoid them to conserve fuel. Therefore, most mission planners launch spacecraft directly into the desired inclination; thus, this minimizes any inclination change required over the duration of the spacecraft life. Most efficient inclination changes are typically achieved at apogee, where orbital velocity  is the lowest.
is the lowest.
 is the lowest.
is the lowest.
Constant-thrust and constant-acceleration trajectories involve a prolonged constant burn. In the limiting case where the vehicle acceleration is high compared to the local gravitational acceleration, the spacecraft points straight toward the target (accounting for target motion), and remains accelerating constantly under high thrust until it reaches its target. In this high-thrust case, the trajectory approaches a straight line. If it is required that the spacecraft rendezvous with the target, rather than performing a flyby, then the spacecraft must flip its orientation halfway through the journey, and decelerate the rest of the way.
In the constant-thrust trajectory, the vehicle's acceleration increases during thrusting period, since the fuel use means the vehicle mass decreases. For constant acceleration, the engine thrust must decrease during the trajectory.
This trajectory requires that the spacecraft maintain a high acceleration for long durations. For interplanetary transfers, days, weeks or months of constant thrusting may be required. As a result, there are no currently available spacecraft propulsion systems capable of using this trajectory. It has been suggested that some forms of nuclear (fission or fusion based) or antimatter powered rockets could do this trajectory.
Main article: Orbit phasing
In astrodynamics orbit phasing is the adjustment of the time-position of spacecraft along its orbit, usually described as adjusting the orbiting spacecraft's true anomaly.
- ^ http://www2.jpl.nasa.gov/basics/bsf4-1.php Basics of Space Flight, Sec. 1 Ch. 4, NASA Jet Propulsion Laboratory
- ^ Walter Hohmann, The Attainability of Heavenly Bodies (Washington: NASA Technical Translation F-44, 1960) Internet Archive.
- ^ Vallado, David Anthony (2001). Fundamentals of Astrodynamics and Applications. Springer. p. 317. ISBN 0-7923-6903-3.
- ^ Sternfeld A., Sur les trajectoires permettant d'approcher d'un corps attractif central à partir d'une orbite keplérienne donnée. - Comptes rendus de l'Académie des sciences (Paris), vol. 198, pp. 711 - 713.
- ^ Belbruno, Edward (2004). Capture Dynamics and Chaotic Motions in Celestial Mechanics: With Applications to the Construction of Low Energy Transfers. Princeton University Press. p. 224.ISBN 978-0-691-09480-9.
- ^ Belbruno, Edward (2007). Fly Me to the Moon: An Insider's Guide to the New Science of Space Travel. Princeton University Press. p. 176. ISBN 978-0-691-12822-1.
- ^ Braeunig, Robert A. "Basics of Space Flight: Orbital Mechanics".
- ^ W. E. Moeckel, Trajectories with Constant Tangential Thrust in Central Gravitational Fields, Technical Report R-63, NASA Lewis Research Center, 1960 (accessed 26 March 2014)
Assume spaceship propulsion system of nuclear fusion which creates numerous energetic particles which can be magnetically "focused" into a consistent stream of particles. This stream of particles is directed in one direction ("exhaust stream") and the ship accelerates in the opposite direction.
While particle accelerators can keep increasing particle speed to near light velocities, nuclear fusion produces particle speed in one burst with no further increase available. This burst can be controlled with regards
Further assume particles have vexch of 10**6 m/sec (1 million meters per sec) which happens to equal .33% c (recall c, light speed, = about 300 million m/s).
At this speed, we can disregard any mass growth due to relativism.
Conserve Momemtum
mv = MV
mexch * vexh = Mship * Vship
--------------......--------------
.....1 sec......................1 sec
mexch/sec = ff exch
vexch = 10**6 m/sec
let vship/sec = Aship = g = 10 m/s**2
Mship = ffexch * 10**6 m/sec / g
Mship = 10**5 ff exch
ffexh / day = 86,400 * ffexch = ffday
delta = daily diff = ffday /Mship = 86,400 ffexch / 100,000 ffexch
delta = .864 = 86.4% ship's initial GW.
Due to selp impaocst constractine ifn this case studey, we won't change vexch because we assume physical limitation of fussion components. therefore, change ship's acceleration (which means bby bye to simulated gravity, and longer more uncofmforatlbe trip, )
thus, let a = .01 g = .1 m/sec**2
Mship = ffxch vexh/aship = ffexch 10**6/.1m/sec**2
ADDED Nov 24, 2010
G-force acceleration will enable routine INTERPLANETARY flights (much like airline travel today: not necessarily a daily event, but readily available) . Thus, trip duration will be just days, and comfortable Earthlike conditions (gravity, atmosphere, comfortable billets, entertainment, etc) will persist throughout the flight.
--------------------------------------------------------------------------------
Perhaps particle accelerators can accelerate sufficient quantity of high speed particles to propel our spaceship in this manner. (Closest current concept: "ion drive" can theoretically accelerate exhaust particles to 5% light speed, c, and reduce interplanetary flight times by a few months.) It'll most likely be a challenge for particle accelerators to accumulate and maintain sufficient supply of plasma (ions); however, once accomplished, accelerators will need to continuously accelerate significant quantities of plasma particles (ions) to speeds approaching 99.9% c.
--------------------------------------------------------------------------------
To enable g-force throughout the trip, we will conduct our own thought experiment. We'll notionalize a propulsion system which can constantly accelerate the vehicles at 10 m/sec2. (Recall that near Earth's surface, objects free fall at this rate.) Perhaps particle accelerators can be designed to accelerate sufficient quantity of high speed particles to propel our spaceship in this manner. (Closest current concept: "ion drive" can theoretically accelerate exhaust particles to 5% light speed, c, and reduce interplanetary flight times by a few months.) It'll most likely be a challenge for particle accelerators to accumulate and maintain sufficient supply of plasma (ions); however, once accomplished, accelerators will need to continuously accelerate significant quantities of plasma particles (ions) to speeds approaching 99.9% c. Spaceflight between planets will take days, and occupants will enjoy simulated gravity throughout entire flight because propulsion systems will carefully expel exact amount of particles to accelerate ships at a constant 10m/sec2. INTERPLANETARY trips will become routine, and this is discussed in depth in following series of articles.
To make them practical for humans and other organisms, some means of constantly accelerating the spacecraft must be implemented. Furthermore, if velocity change is kept at a constant 10 meters per second per second, vessel occupants will be "pressed" against the spacecraft hull with the same pressure they now feel on Earth's surface; thus, simulating gravity. In-flight times would greatly decrease; i.e., current best flight time to Mars is six months; current G-force acceleration would decrease this flight time to 4 days.
This first volume proposes a propulsion system with particle accelerators to constantly accelerate the vehicles at ten meters per second per second (10 m/s/s). This capability would enable trips between planets to take days and weeks versus the months and years that it now takes with constant velocity.Achieving constant "g" acceleration will enable occupants to enjoy simulated gravity throughout entire flight because propulsion systems will carefully expel exact amount of plasmas particles (ions) to accelerate ships at a constant 10 m/sec2. (Recall that near Earth's surface, gravity causes objects to fall at 9.80665 m/sec2.) It'll be a challenge for accelerator driven vessels to accumulate sufficient fuel (plasma ions) to make the trip. However, once accomplished, accelerator reliability will need to be the best ever achieved. They will need to perform long and strong; propulsion systems must continuously accelerate significant ion quantities to speeds approaching 99.9% light speed, c. (Closest current concept: "ion drive" can theoretically accelerate exhaust particles to 5% c.)
Source Doct: http://www2.jpl.nasa.gov/basics/bsf4-1.php
Orbiting between planets, minimize the propellant mass needed by your spacecraft and its launch vehicle
Hohmann Transfer Orbits
From Earth to Mars, current conditions compel us to minimize fuel burns, and the Hohman Transfer can do this.Consider that an Earth bound spacecraft is already in Earth's solar orbit. To travel to Mars, the spacecraft's existing solar orbit must be adjusted. The desired orbit's perihelion (closest distance to the sun) will be at Earth's orbit, and the aphelion (farthest from the sun) will be at Mars' orbit. This is called a Hohmann Transfer orbit. The portion of the solar orbit from Earth to Mars is called its trajectory.
To transfer from Earth orbit to Mars orbit, increase the apoapsis (aphelion) of the spacecraft's present solar orbit. Since Earth orbit is at periapsis, we must use propulsion system to accelerate in the direction of Earth's revolution around the sun. The acceleration is tangential to the existing orbit. To determine correct amount of propulsion, see the Rocket & Space Technology website. After this brief "burn", the spacecraft simply coasts to orbit of Mars.
Earth to Mars via Least Energy Orbit

To rendezvous with planet, Mars, requires precise timing for orbital insertion (into transfer orbit) for spacecraft to arrive at the Martian orbit exactly when Mars is there. The opportunity to launch a spacecraft on a minimum-energy transfer orbit to Mars happens about every 25 months.
To enter a Martian orbit, the spacecraft must then decelerate relative to Mars using a retrograde rocket burn or some other means. To land on Mars from orbit, as did Viking, the spacecraft must decelerate even further using a retrograde burn to the extent that the lowest point of its Martian orbit will intercept the surface of Mars. Since Mars has an atmosphere, final deceleration may also be performed by aerodynamic braking direct from the interplanetary trajectory, and/or a parachute, and/or further retrograde burns.
Inward Bound
To return to Earth from an outer planet such as Mars, the spacecraft must accelerate opposite the direction of Earth's revolution around the sun, thereby decreasing its orbital energy. Of course the spacecraft will continue going in the same direction as Earth orbits the sun (counter clockwise as observed from north of Sol), but a little slower now. Again, the spacecraft must insert into its interplanetary trajectory at the correct time.Type I and II Trajectories
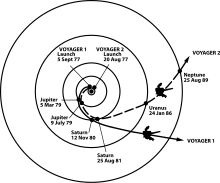
If the interplanetary trajectory carries the spacecraft less than 180 degrees around the sun, it's called a Type-I Trajectory. If the trajectory carries it 180 degrees or more around the sun, it's called a Type-II. Consider Voyager 2, which toured the Jovian planets. The spacecraft was launched on a Type-II Hohmann transfer orbit to Jupiter. Had Jupiter not been there at the time of the spacecraft's arrival, the spacecraft would have fallen back toward the sun, and would have remained in elliptical orbit as long as no other forces acted upon it. Perihelion would have been at 1 AU, and aphelion at Jupiter's distance of about 5 AU.
Consider Voyager 2, which toured the Jovian planets. The spacecraft was launched on a Type-II Hohmann transfer orbit to Jupiter. Had Jupiter not been there at the time of the spacecraft's arrival, the spacecraft would have fallen back toward the sun, and would have remained in elliptical orbit as long as no other forces acted upon it. Perihelion would have been at 1 AU, and aphelion at Jupiter's distance of about 5 AU.
However, Voyager's arrival at Jupiter was carefully timed so that it would pass behind Jupiter in its orbit around the sun. As the spacecraft came into Jupiter's gravitational influence, it fell toward Jupiter, increasing its speed toward maximum at closest approach to Jupiter. Since all masses in the universe attract each other, Jupiter sped up the spacecraft substantially.
The spacecraft passed on by Jupiter since Voyager's velocity was greater than Jupiter's escape velocity, and of course it slowed down again relative to Jupiter as it climbed out of the huge gravitational field. The speed component of its Jupiter-relative velocity outbound dropped to the same as that on its inbound leg.
But relative to the sun, it never slowed all the way to its initial Jupiter approach speed. It left the Jovian environs carrying an increase in angular momentum stolen from Jupiter. Jupiter's gravity served to connect the spacecraft with the planet's ample reserve of angular momentum. This technique was repeated at Saturn and Uranus.The vector diagram on the left shows the spacecraft's speed relative to Jupiter during a gravity-assist flyby. The spacecraft slows to the same velocity going away that it had coming in, relative to Jupiter, although its direction has changed. Note also the temporary increase in speed nearing closest approach.
Enter the Ion Engine
 All of the above discussion of interplanetary trajectories is based on the use of today's system of chemical rockets, in which a launch vehicle provides nearly all of the spacecraft's propulsive energy. A few times a year the spacecraft may fire short bursts from its chemical rocket thrusters for small adjustments in trajectory. Otherwise, the spacecraft is in free-fall, coasting all the way to its destination. Gravity assists may also provide short periods wherein the spacecraft's trajectory undergoes a change.But ion electric propulsion, as demonstrated in interplanetary flight by Deep Space 1 - and employed on the Dawn science mission to the asteroids - works differently. Instead of short bursts of relatively powerful thrust, electric propulsion uses a more gentle thrust continuously over periods of months or even years. It offers a gain in efficiency of an order of magnitude over chemical propulsion for those missions of long enough duration to use the technology. Ion engines are discussed further under Propulsion in Chapter 11.
All of the above discussion of interplanetary trajectories is based on the use of today's system of chemical rockets, in which a launch vehicle provides nearly all of the spacecraft's propulsive energy. A few times a year the spacecraft may fire short bursts from its chemical rocket thrusters for small adjustments in trajectory. Otherwise, the spacecraft is in free-fall, coasting all the way to its destination. Gravity assists may also provide short periods wherein the spacecraft's trajectory undergoes a change.But ion electric propulsion, as demonstrated in interplanetary flight by Deep Space 1 - and employed on the Dawn science mission to the asteroids - works differently. Instead of short bursts of relatively powerful thrust, electric propulsion uses a more gentle thrust continuously over periods of months or even years. It offers a gain in efficiency of an order of magnitude over chemical propulsion for those missions of long enough duration to use the technology. Ion engines are discussed further under Propulsion in Chapter 11.
Click the image above for more information about Deep Space 1. The Japan Aerospace Exploration Agency's asteroid explorer HAYABUSA also employed an ion engine. Even ion-electric propelled spacecraft launch form Earth's surface via chemical rockets. Fortunately, ion engines are more efficient then chemical engines; thus, they can be less massive, and require less powerful launch vehicles. Initially, then, the trajectory of an ion-propelled craft may look like the Hohmann transfer orbit. But over long periods of continuously operating an electric engine, the trajectory will no longer be a purely ballistic arc.Enter the Ion Engine
 All of the above discussion of interplanetary trajectories is based on the use of today's system of chemical rockets, in which a launch vehicle provides nearly all of the spacecraft's propulsive energy. A few times a year the spacecraft may fire short bursts from its chemical rocket thrusters for small adjustments in trajectory. Otherwise, the spacecraft is in free-fall, coasting all the way to its destination. Gravity assists may also provide short periods wherein the spacecraft's trajectory undergoes a change.But ion electric propulsion, as demonstrated in interplanetary flight by Deep Space 1 - and employed on the Dawn science mission to the asteroids - works differently. Instead of short bursts of relatively powerful thrust, electric propulsion uses a more gentle thrust continuously over periods of months or even years. It offers a gain in efficiency of an order of magnitude over chemical propulsion for those missions of long enough duration to use the technology. Ion engines are discussed further under Propulsion in Chapter 11.
All of the above discussion of interplanetary trajectories is based on the use of today's system of chemical rockets, in which a launch vehicle provides nearly all of the spacecraft's propulsive energy. A few times a year the spacecraft may fire short bursts from its chemical rocket thrusters for small adjustments in trajectory. Otherwise, the spacecraft is in free-fall, coasting all the way to its destination. Gravity assists may also provide short periods wherein the spacecraft's trajectory undergoes a change.But ion electric propulsion, as demonstrated in interplanetary flight by Deep Space 1 - and employed on the Dawn science mission to the asteroids - works differently. Instead of short bursts of relatively powerful thrust, electric propulsion uses a more gentle thrust continuously over periods of months or even years. It offers a gain in efficiency of an order of magnitude over chemical propulsion for those missions of long enough duration to use the technology. Ion engines are discussed further under Propulsion in Chapter 11.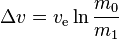
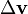 ).
).



0 Comments:
Post a Comment
<< Home