REFERENCE: Momentum Basics

LIST OF TABLES

Select from following: Momentum - Basics TABLE-1: Consistent units. TABLE-2: Convert Exhaust Velocity to decimal c.TABLE-3: Convert Ship's Mass to metric Tonnes (mT)TABLE-4: Convert to RatesFurther StudySummary

Momentum Basics

Momentum is mass times velocity. It typically uses symbol: "p". p = m * v p = (2.0 kg)(4.0 m/s) p = 8.0 kg-m/s Thus, we calculate this object's momentum to be 8.0 kg-m/s. Momentum's dimensions are kg-m/s, pronounced: 'kilogram meter per second'. Like velocity, momentum is a vector; it has a magnitude as well as a direction. In fact, they both have the same direction. That is, if an object has a velocity due north, then its momentum will also be due north. However, momentum is both mass times velocity. Momentum is directly proportional to velocity. Change the velocity of an object by a factor of 1/4, then momentum would also change by 1/4. Momentum is also directly proportional to mass. With constant velocity, momentum varies with the mass. Example: triple the mass of an object, then the momentum also triples. Momentum is a conserved quantity. Within a closed system of interacting objects, total momentum of entire system maintains a constant. When object A collides with object B in an isolated system, the total momentum of the two objects before the collision is the same as the total momentum after the collision. Any momentum lost by object A goes to object B.

Thus, total momentum of a system of objects is "conserved"; total amount of mass times velocity is static. To further understand momentum conservation, consider Newton's Law of Momentum Conservation. When two objects collide, the forces acting between the two objects are equal in magnitude and opposite in direction. In equation form, m*v = -M * V. The forces between the two objects are equal in magnitude and opposite in direction, which leads to Newton's Law of Momentum Conservation. In a collision, the momentum change of object A is equal and opposite to the momentum change of object B. That is, the momentum lost by object A is equal to the momentum gained by object B. In a collision between two objects, one object slows down and loses momentum while the other object speeds up and gains momentum. If object A loses 75 units of momentum, then object B gains 75 units of momentum. Yet, the total momentum of the two objects (object A plus object B) is the same before the collision as it is after the collision; the total momentum of the system (the collection of two objects) is conserved. For any collision occurring in an isolated system, momentum is conserved - the total amount of momentum of the collection of objects in the system is the same before the collision a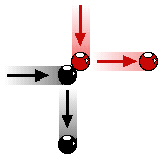s after the collision. Momentum can be readily observed by watching billiard balls collide.

Similarly, high velocity gas goes in one direction, and rocket goes in opposite direction. Action causes reaction.

Recall momentum exchange: M * V = m * v
Rocket and jets propel themselves due to momentum transfer where high speed exhaust particles move a much larger vehicle in the opposite direction to a much slower but still useful speed. This momentum exchange between fast moving fuel particles and a slow moving spaceship can be expressed:

M_ship * V_ship = m_fuel * v_fuel

First, we choose to increase the speed of a large space vessel by 10 m/s in one second. Thus, set V_ship be a constant 10 m/s. This relates to the approximate value of g = 10 m/s² acceleration due to gravity near Earth’s surface. Thus, assume our notional spaceship can expel enough high speed particles to increase velocity an additional 10 m/s for every second of spaceflight. The resultant force will simulate Earth-like gravity for ship and contents.
2nd, we further choose to expend one gram of particles in one second. I.e., set m_fuel to be a constant 1.0 gram for convenience.
3rd, our thot experiment uses an onboard particle accelerator to give these fuel particles extremely high speeds. Since current devices easily accelerate particles to 99% of light speed, our thought experiment will compare sustainable fuel exhaust velocity, v_fuel, to light speed, c. Furthermore, we now choose to name v_Exh to more clearly indicate exhaust velocity of particles exiting vessel. Finally, we choose to independently vary v_Exh by incrementally increasing from row to row in the following tables. Thus, v_Exh is our Independent Variable (IV).
4th, solve for the remaining term, M_ship, mass of ship, to determine how much ship can be propelled 10 m/s by a certain amount of fuel mass exiting vehicle at high speed in opposite direction of travel. Since M_ship depends on the value of v_Exh, M_ship is our Dependent Variable (DV).

M_ship = m_fuel * v_Exh / V_ship

(Note: Following tables will consider only Newtonian concepts and will disregard relativistic mass increase for now. Relativistic mass growth will be considered later.)

---

TABLE-1. Consistent units.

Mship = mfuel * vExh / Vship
Mship	Vship	mfuel	vExh
Ship's Mass	ship's vel	fuel mass	exhaust vel
Grams	m/s	grams	m/s
1,000,000	10.0	1.0	10,000,000
2,000,000	10.0	1.0	20,000,000
3,000,000	10.0	1.0	30,000,000
DV	Const.	Const.	IV

Grams and m/s are consistently used on both sides of equation.

While above calculations are straight forward, two terms have a lot of digits which might prove inconvenient. We can streamline this process through a conversion contant.

---

TABLE-2. Express v_Exh as d_c * c; decimal c times light speed
For convenience, use a mix different velocity units. In particular, we'd like to continue expressing ship's velocity increase ,V_ship, as 10 meters per second; but we'd like to change v_Exh from m/s to decimal light speed, d_c c, where d_c is decimal component of particle exhaust speed expressed in terms of light speed.
Recall light speed is approximately 300 million meters per second, c = 300,000,000 m/s.
Thus, Table-1 proposes example value for v_Exh of .1 c, 30,000,000 m/s = 10% c. (Note: Disregard relativity effects for now; we'll discuss that later).

v_Exh as decimal c

Mship = mfuel * K2 * vExh/ Vship
K1 = 300,000,000
Mship	V ship	m fuel	vExh
Ship's Mass	ship's vel	fuel mass	exhaust vel
Grams	m/s	grams	dc c
3,000,000	10.0	1.0	.1 c
6,000,000	10.0	1.0	.2 c
9,000,000	10.0	1.0	.3 c
12,000,000	10.0	1.0	.4 c
DV	Const.	Const.	IV

Consistent values requires conversion constant. Note that V_Exh has equivalent values in last row of Table 1. and first row of Table 2. For consistent M_ship, determine conversion constant K₂ such V_Exh can be expressed as decimal light speed.

---

TABLE-3. Convert M_ship to metric Tonnes (mT) By definition: 1 mT = 1,000,000 gms; thus, example value of M_Ship=3,000,000 gms = 3 mT.

K3=
Mship * Vship 


mfuel * vExh
= 
3mT * 10m/s 


1 gm * .1c
= 
3 


c

Thus, k3 = 3/c, given following set of dimensions: mfuel as grams (gm) vfuel as dc c Mship as metric Tonnes (mT) Vship as meters per second (m/s)

M_ship in mT

Mship = K3 * mfuel * vExh / Vship

K₃ = 3/c

M_ship

V_ship

m_fuel

v_Exh

Ship's Mass

ship's vel

fuel mass

exhaust vel

metric tons

m/s

grams

d_c c

3.0

10.0

1.0

.10 c

4.5

10.0

1.0

.15 c

6.0

10.0

1.0

.20 c

7.5

10.0

1.0

.25 c

9.0

10.0

1.0

.30 c

10.5

10.0

1.0

.35 c

12.5

10.0

1.0

.40 c

13.5

10.0

1.0

.45 c

DV

Const.

Const.

IV

---

TABLE-4. Convert to Rates Changing to mixed units affects the terms: v_Exh and M_ship; thus, unaffected terms (V_ship and m_fuel) keep the same dimensions. However, those terms (V_ship and m_fuel) can be usefully converted to rates.
Start with the original ship-fuel momentum equation:

Mship * Vship	=	mfuel * vExh

and divide both sides by one second:

Mship * Vship 


1 second
= 
mfuel * vExh 


1 second

Next, we'll arbitrarily rearrange as follows:

Mship * 
Vship


1 sec
= 
mfuel


1 sec
* vExh

Since definition of acceleration is velocity increase per time, V_ship per second is an acceleration. We've chosen V_ship to be 10 m/s, same value as g, acceleration due to Earth's surface gravity. Thus, we can rearrange equation as follows:

M_ship * g = (m_fuel/1 sec) * v_Exh

Further, we can introduce new term, fuel flow per sec (ff_sec), and substitute for the expression: m_fuel /sec. Thus, far we've arbitrarily chosen the value of 1 gram per second for convenience, but we will eventually use this term for any value.

M_ship * g = ff_sec * v_Exh

Mship * Vship 1 sec = 300 * vExh mfuel 1 sec Using previous logic: restate Vship/sec as g, gravity caused acceleration. restate mfuel/sec as ffsec, fuel flow per second; restate vExh as dcc, decimal light speed. rearrange: Mship = k * ffsec * dc c g

Mship = K * ffsec * vExh / g K = 30 g/c M ship g ffsec vExh Ship's Mass Gravity fuel flow exhaust vel metric tons m/s2 gm/sec dc c 6.0 10.0 1.0 .20 c 7.5 10.0 1.0 .25 c 9.0 10.0 1.0 .30 c 10.5 10.0 1.0 .35 c 12.0 10.0 1.0 .40 c 13.5 10.0 1.0 .45 c 15.0 10.0 1.0 .50 c 16.5 10.0 1.0 .55 c DV Const. Const. IV

k =	Mship * g ffsec * dcc	=	3 mT * g 1 gm/sec * .1c	=	30 g c

Thus, we've taken the Momentum Conservation equation and applied it for a duration of one second. For space travel to become routine, technology will have to accomplish two things:
1. Micro-scale. Spread the amount of fuel ejected in a smooth continuous manner throughout the entire second.
2. Macro-scale. Reliably repeat above item for each of the 86,400 seconds during each day of space flight.
Both above items are easily done now in various modes of transportation, but can they be done for particles accelerated to large portions of c, speed of light???

Summary

Consistent Units

Give terms following values: mfuel = 1.0 gram Vship = 10 meters / second vExh= 30,000,000 m/s Then Mship = (1.0 gm * 30,000,000 m/s) / (10 m/s) Mship= 3,000,000 gm

Basic Momentum M = mfuel * vExh/ Vship Mship mfuel Vship vfuel gm gm m/sec m/s 3,000,000 1.0 10 30,000,000

Mixed Units

Conversion Constant: 300 Mship = (300)(mfuel * vExh / Vship) Mship mfuel Vship vExh mT gm m/sec dc c 3 1.0 10 .1 c 6 1.0 10 .2 c

1,000,000 gms = 1,000 kgms = 1.0 metric Tonnes = 1 mT Thus, Mship = 3,000,000 gm = 3.0 mT 300,000,000 meters /sec = light speed = c Thus, VExh= 30,000,000 m/s = .1c It’s more convenient to express Mship in mT and vExhin decimal c. To do this, introduce a conversion constant, k3, as follows: Mship = k3 * mfuel * vExh / Vship

where k₃ = 300

Rates

Convert to ffsec Fuel Flow/sec g ffsec vExh Mship con con IV DV m/s2 gm/sec dc c mT 10 1 0.1 c 3 10 1 0.2 c 6 10 1 0.3 c 9 Particle velocity, vExh, of .1 c contributes sufficient momentum so that one gram of exhaust particles can propel a 3 ton vessel to an additional 10 m/sec. Since momentum is directly proportional to velocity, increasing vExh another .1 c will propel another 3mT of ship's mass.

Recall: mfuel * vExh = Mship * Vship. Divide both sides by one sec: mfuel * vExh 1 sec = MShip * vShip 1 sec Rearrange: mfuel 1 sec * vExh = MShip * vShip 1 sec Recall that we set Vship equal to 10 m/s; thus, Vship/ 1sec = 10m/s/s = g, acceleration due to gravity near Earth’s surface. Introduce new term, fuel flow per second: ffsec = mfuel/sec. Thus, we substitute to get: ffsec* vExh = Mship * g To continue expressing vExh as decimal c and Mship in metric Tonnes, we'll introduce conversion constant, k = 300/c. Thus, k * vExh = 300 * dc. Mship = 300 * ffsec * dc g

Further Study, Related Concepts: Impulse and Specific Impulse

---

ImpulseThe Physics Classroom In physics, the quantity Force*time is known as the impulse. And since the quantity m*v is the momentum, the quantity m*"Delta "v must be the change in ...www.physicsclassroom.com/Class/momentum/U4L1b.html - 48k - Cached - Similar pages Physics - Impulse - Martin Baker Physics - Impulse. Impulse is the integral of force over time, it is measured in Newton-seconds. For instance a force of one Newton applied over one second ...www.euclideanspace.com/physics/dynamics/collision/impulse/index.htm - 26k - Cached - Similar pages SparkNotes: SAT Physics: Impulse SAT II Physics may also present you with a force vs. time graph, and ask you to calculate the impulse. There is a single, simple rule to bear in mind for ...www.sparknotes.com/testprep/books/sat2/physics/chapter9section2.rhtml - 32k - Cached - Similar pages Impulse -- from Eric Weisstein's World of Physics An impulse is an instantaneous change in momentum. which can be found by integrating a force F over a characteristic time , giving ...scienceworld.wolfram.com/physics/Impulse.html - 12k - Cached - Similar pages Impulse In everyday language, an impulse is something you have - "I just had an impulse, so I bought a new coat." In physics, an impulse is something else (you ...www.batesville.k12.in.us/physics/PHYNET/Mechanics/Momentum/impulse.htm - 6k - Cached - Similar pages Momentum Lesson 1: The Impulse Momentum Change Theorem ... Momentum is a physics term; it refers to the quantity of motion that an object has. ...www.glenbrook.k12.il.us/GBSSCI/PHYS/CLASS/momentum/u4l1a.html - 15k - Cached - Similar pages Physics Zone: Impulse (When Push Comes to Shove) The product of average net force and change in time is called Impulse. The formula for it actually comes from a little manipulation of Newton's Second Law. ...regentsprep.org/Regents/physics/phys01/impulse/default.htm - 3k - Cached - Similar pages Physics Help: Impulse Impulse is change in momentum and results from force acting over a period of time. ... Impulse in Physics Problems. Impulse and Momentum ...www.physics247.com/physics-help/impulse.shtml - 11k - Cached - Similar pages Impulse Physics Hive Assault: Impulse Physics. Dynamic Animation Calculations in Hive Assault Real-time Calculation of Bone Impulse Reactions from Weapons ...www.owlnet.rice.edu/~comp460/PRSite/tech/impulse.htm - 9k - Cached - Similar pages FHSST Physics Momentum:Impulse - Wikibooks, collection of open ... FHSST Physics Momentum:Impulse ... [edit] Worked Example 36 Impulse and Change in momentum. Question: A 150 N resultant force acts on a 300 kg object. ...en.wikibooks.org/wiki/FHSST_Physics_Momentum:Impulse - 28k - Cached - Similar pages

---

Specific Impulse
Specific impulse - Wikipedia, the free encyclopedia Specific impulse (usually abbreviated Isp) is a way to describe the efficiency of rocket and jet engines. It represents the impulse (change in momentum) per ...en.wikipedia.org/wiki/Specific_impulse - 33k - Cached - Similar pages Variable specific impulse magnetoplasma rocket - Wikipedia, the ... The variable specific impulse magnetoplasma rocket (VASIMR) is a hypothetical form of spacecraft propulsion that uses radio waves and magnetic fields to ...en.wikipedia.org/wiki/Variable_specific_impulse_magnetoplasma_rocket - 20k - Cached - Similar pages[ More results from en.wikipedia.org ] Specific Impulse We can divide this equation by the weight of the propellants to define the specific impulse. The word "specific" just means "divided by weight". ...www.grc.nasa.gov/WWW/K-12/airplane/specimp.html - 13k - Cached - Similar pages What is specific impulse? Specific impulse is the change in momentum per unit mass for rocket fuels, or rather how much more push accumulates as you use that fuel. ...www.qrg.northwestern.edu/projects/vss/docs/Propulsion/3-what-is-specific-impulse.html - 5k - Cached - Similar pages How do you calculate specific impulse? To calculate the specific impulse, we first need to calculate the exhaust velocity. Since the real exhaust velocity is exceeding complex to calculate, ...www.qrg.northwestern.edu/projects/vss/docs/Propulsion/3-how-you-calculate-specific-impulse.html - 7k - Cached - Similar pages Rocket Engine Specific Impulse Program Specific Impulse (Isp) is a measure of the “fuel efficiency” of a rocket. The necessary thermodynamic calculations for Isp are performed by a package of ...www.dunnspace.com/isp.htm - 183k - Cached - Similar pages
Specific Impulse Inc. Information Architecture, Web Development ... Specific Impulse: Information Architecture, Web Site Design, and Intranet and Web Site Management Solutions.www.si9.com/ - 22k - Cached - Similar pages NASA Tech Briefs - Variable-Specific-Impulse Magnetoplasma Rocket NASA Tech Briefs, This rocket is expected to enable long-term human exploration of outer space. Johnson Space Center has been leading the development of a ...www.techbriefs.com/content/view/1768/32/ - 41k - Cached - Similar pages PROPELLANTS Chemical propellants in common use deliver specific impulse values ranging from about 175 up to ... Specific impulse of some typical chemical propellants 1 ...www.hq.nasa.gov/office/pao/History/conghand/propelnt.htm - 16k - Cached - Similar pages

Peripheral Energy Requirements

While this seems like a great way to quickly increase inflight performance, this comes at the cost of enormous energy. It's a fact of nature; it's not necessarily free. Consider a gasoline powered automobile. The fuel converts to energy, but not all the energy rotates the wheels; a significant portion of the energy from the exploding gasoline pushes the pistons and rotates the drive shafe. Eventually, some of the gas's energy results in rotary motion pushing the wheels which touch the road and propel the auto forward. Furthermore, some energy must be diverted for peripheral uses: radio, air conditioning, etc.. However, the essential diversion of energy goes to the auto's generator (or alternator) which converts motion into electricity to the spark plugs which explode subsequent gasoline vapors to produce more motion and so on. We can call this an energy cycle.In like manner, our spaceship's propulsion system must have a similar energy cycle. It must be designed so the system diverts some energy from the accelerator's output to create more plasma and charge the magnets to propel more ions to keep the cycle continuing.Thus far, we've taken the Momentum Conservation equation and applied it for a duration of one second. For space travel to become routine, technology will have to accomplish two things: Micro-scale. Spread the amount of fuel ejected in a smooth continuous manner throughout the entire second. Macro-scale. Reliably repeat above item for each of the 86,400 seconds during each day of space flight. Both above items are easily done now in various modes of transportation, (for example, the typical plane, train, and automobile have done this for many years). However, can micro/macro scale energy conversion be done for exhaust particles accelerated to large portions of c, speed of light??? Note: for current state of nuclear propulsion, see excellent book,Nuclear Space Power and Propulsion Systems (Progress in Astronautics and Aeronautics) by Claudio Bruno(Editor) --------------------------------------------------------------------------------On the other hand, thought experiment further assumes onboard fuel is consumed at fuel's original size. Thus, inflight gross weight of the vehicle will be ever decreasing due to continuous fuel consumption which will be computed by time, t, times original fuel flow, ffsec.