Destinations in 3D

CONTENTS Interplanetary: 2-D ModelQuads: 2-D CoordinatesLocal NeighborhoodEight Closest NeighborsPosition Vector to Sirius

Stellar destinations require a 3 dimensional (3-D) model.

---

---

---

This contrasts starkly with interplanetary destinations which can get by with a 2-D model. 

To map a planet's current location , one just needs to determine planet's current Right Ascension (RA or α), distance remains fairly constant since most planets orbit Sol in a near perfect circle (elliptical eccentricity ≈ 0).  For simplicity, Thought Experiment (TE) arbitrarily assumes all planetary orbits to be circular as well as coplanar. 
In fact, each planetary orbit occupies a plane uniquely inclined to the Celestial Equatorial Plane (CEP) which means most planetary positions are always slightly above/below CEP. Thus, interplanetary travelers will certainly consider these planetary vertical distances; however, they are quite small when compared to stellar dimensions and can be ignored in regards to an interstellar model.

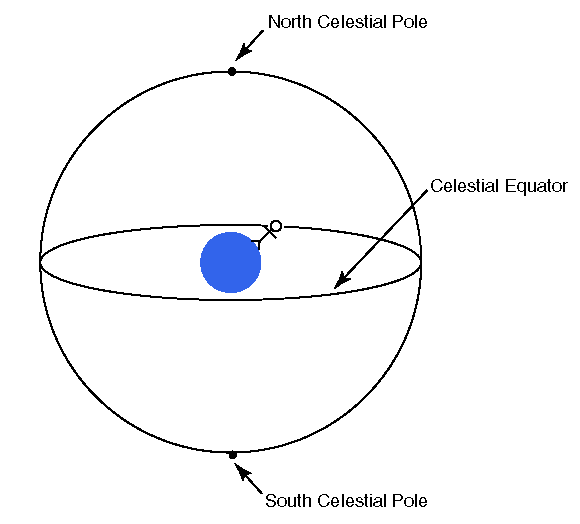Celestial Equator projects Earth's Equator into space. Thought Experiment (TE) uses the term, Celestial Equatorial Plane (CEP), to indicate the plane defined by the celestial equator.  For simplicity, TE arbitrarily assumes all planets to reside on CEP.  (In fact, even the Earth's orbital plane,  ecliptic, is inclined to the CEP.  However, the offset from CEP is slight when compared to stellar dimensions).

Right Ascension.  (RA or "α") is celestial "longitude". Much like terrestrial longitude, RA increases in value as one travels away from the zero value. RA increases in a counter clockwise (easternly) direction from Aries (♈). α is customarily measured in hours(h), minutes(m), and seconds(s), while a circular arc is measured in degrees(°), minutes(') and seconds("). (Recall: 24 hours equals a full circle (360°); thus, 1h of RA equals 15° of arc; 1m of RA equals 15' of arc; and 1s equals 15" of arc. Due to their orbital motion, each planet's RA is ever changing in a fairly rapid manner.

Aries (♈) is commonly used as the reference for RA (α = 0°). ♈ marks Earth's position in its orbit during the Vernal Equinox. This is the date (around March 21) when Earth bound observers note the Sun crossing the celestial equator from south to north. This is commonly considered as one of the two annual dates where duration of day equals that of the night (e.g., "equi-nox" = "equal night").

Quickly Approximate Location 1. Assume Near-Circular Orbits. For simplicity, TE assumes circular orbits at an constant distance from Sol. For example, we assume that Jupiter is always about 5 AU from Sol . (As a matter of fact, none of the planetary orbits are exactly circular; eccentricities vary from .007 to 0.2.)  2. Line of Position (LOP). Given a circular orbit, planet's RA can determine a planet's location because a RA measurement (0 to 360°) can be represented by a Line of Position (LOP) as shown. The subsequent intersection with its orbit quickly determines planet's position(with respect to CEP).

2-D Cartesian Quadrants On the CEP, arbitrarily divide interplanetary space into four quadrants as shown. Align Cartesian, X-Y, axii such that the ray, RA = 0°, is the positive X axis and the ray, RA= 90°, is the positive Y axis. Thence, indicate the four traditional Cartesian quadrants as shown; each with their unique combination of signs for (X, Y) values.  By simple inspection, we note Jupiter to be in Quadrant-IV in this instance; however, all planets move through all the quadrants.

---

Extrasolar planets. While all stellar neighbors should be visited for firsthand observations, perhaps the initial destinations should be the ones where local observations indicate most favorable conditions. Examples:

• Earth like planets in best orbits around M-class stars.
• Existence of asteroids and comets.

---

Local Stellar Neighborhood 

There are 61 known stars (and 7 brown dwarf stars) within 17 Light Years (LYs) from Sol,
our home star (aka "Sun").  

---

These 68 objects are grouped into 50 stellar systems. 

---

In spite of being relatively close, only nine can be observed with the naked eye.

---

 The map shows the closest 32 systems.

---

As an example, consider one of them in more detail.

---

	Due to its proximity and size, Sirius appears as the brightest night time star to Earthbound observers. Modern telescopes show it to be a binary star system: a white main sequence star (Sirius A), and a faint white dwarf companion(Sirius B). The distance between them varies from 8.1 to 31.5 AU.  Known as the "Dog Star" to Westerners, Sirius provided a key navigation aid for the Polynesians as they paddled their outriggers around the vast Pacific Ocean.
	Star Right Ascension (α) Name Hrs Min Sec Dec Deg Sirius 6h 45m 8.9s 101.29° Convert α to Decimal Degrees α = Hr*15 + Mn/4 + Sec/240 Right Ascension (RA) to Sirius is the angle (101.29°) from Aries to the LOP to Sirius. This is shown on an overhead view of the Celestial Equatorial Plane (CEP). Note this view eliminates perspective; thus, the distances of 5 and 10 LYs can now be shown as circles and not ellipses.  While planetary RAs change daily, star movements take centuries to be discerned by the human eye. Thus, TE considers stellar RAs to be static.
	Declination (δ) Deg Min Sec Dec Deg -16° 42' 58" -16.72° Convert δ to Decimal Degrees δ = Deg + Mn/60 +Sec/3600 Declination  (δ) is measured in degrees north and south of the CEP. Values vary from +90° to −90°. Declination to Sirius is -16.72° as shown on this edge-on view of the CEP. LOP is lowered from its RA position on CEP to position of Sirius beneath the CEP.

Dist. (d)  Light-Years 8.583 LY Observed .Stellar Distance  can be measured through a variety of methods. Standard candles and parallax can determine stellar distances up to 1,600 LYs away

Position Vector from Sol to Sirius  can be drawn in a vertical plane as shown. This plane is perpendicular to the Celestial Equatorial Plane (CEP) and aligned with the Right Ascension (RA) angle (101.29°). Simple trig identities can resolve this vector into two components: Z: vertical vector from CEP to position of Sirius directly beneath CEP.  dCEP: distance to Sirius projected onto CEP.

Star Dec (δ) Dist. (d)  dCEP Z Name Deg LYs LY LY Sirius -16.7° 8.583 8.22 -2.47 Observed d*cos(δ) d*sin(δ) √(d2CEP + Z2 ) = d

Star RA(α) dCEP X Y Name Deg LY LY LY Sirius 101.3° 8.22 -1.61 8.06 Observed d*cos(δ) dCEP*cos(α) dCEP*sin(α) dCEP = √(X2 + Y2)

RA Vector from Sol to Sirius  is best shown on an overhead view of the CEP. This 2-D view shows Sirius projected onto the CEP from it's 3-D location light years beneath the CEP. Simple trig identities can resolve RA vector to: X: portion of Sirius position along the X-axis.  Y: portion of Sirius position along the Y-axis.

Sirius: 3-D Coordinates

Combining all information from above, we can take observations (R.A., Dec and Distance) of Sirius's position and determine Cartesian coordinates (X, Y, Z). We arbitrarily choose Sol as the reference point (aka "origin").

	Star	Right Ascension (α)				Declination (δ)				Dist. (d)	3-D Cartesian Coord.
	Name	Hrs	Min	Sec	Deg	Deg	Min	Sec	Deg	Light-Years	dCEP	X	Y	Z
	Sol	0h	0m	0s	0.0°	0°	0'	0"	0.0°	0.0 LY	0.00	0.00	0.00	0.00
	Sirius	6h	45m	8.9s	101.29°	-16°	42'	58"	-16.72°	8.583 LY	8.22	-1.61	8.06	-2.47
	System	Convert α to Decimal Degrees				Convert δ to Decimal Degrees				Observed	d*cos(δ)	dCEP*cos(α)	dCEP*sin(α)	d*sin(δ)
		α = Hr*15 + Mn/4 + Sec/240				δ = Deg + Mn/60 +Sec/3600					d = X2 + Y2 + Z2

---

Travel Time

To approximate travel time to nearby stars, Thought Experiment (TE) proposes an heuristic which might be achieved given some reasonable assumptions.

1. TE assumes slight advances in current technology allow for large spacecraft to use particle accelerators as propulsion systems. TE further assumes these onboard accelerators will expel exact quantity of plasma particles at near light speeds to accelerate the vessel for a "g-force" such that onboard passengers and crew will experience an Earth like gravity.  This assumption leverages Einstein's "Thought Experiment" where people onboard an accelerating elevator (at 9.8 m/s²) would feel same force as if they were static on Earth's surface. (This is sometimes called the "Equivalence Principle".)
2. TE assumes constant g-force acceleration can bring the vessel to very high velocities; thus, operational requirements compel the vessel to decelerate the vessel at the end of the voyage (reverse the direction of the g-force vector). If the flight plan calls for constant g-force throughout the flight, then the deceleration duration must equal the acceleration duration. In subsequent work, TE shows that one year of g-force acceleration can take the vessel to approximately .644 light speed (c) after the vessel travels a distance of 0.38 LY. Thus, the flight plan requires vessel to start deceleration at about .38 LY from destination for about one year's time.  Thus, one year's acceleration plus one year's deceleration account for about .76 LY; however, the closest stellar neighbor is over 4 LY away.
3. TE assumes g-force's plasma acceleration will convert considerable quantities of mass to energy. In fact, preliminary research indicates fuel requirements could easily exceed entire gross weight of vessel; thus, TE considers impractical (if not impossible) to g-force power the vessel for entire distance to destination star. Thus, TE arbitrarily assumes a duration of one year for acceleration plus another year for deceleration.  Thus, TE's flight plan will require a long cruise period between acceleration phase and deceleration phase. 
4. TE assumes during cruise phase, Earth like gravity will be simulated via carefully controlled longitudinal spin of the vessel.  Cruise duration (as observed from Earth) can be computed by a simple motion equation as shown below.  Crew/pax will experience much shorter cruise duration due to relativity.
5. TE assumes flight profile from Sol to Sirius to be modeled as follows:

Acceleration:  time = tAcc = 1 year; distance = dAcc= .38 LY

Deceleration:  time = tDec = 1 year; distance = dDec= .38 LY

Cruise: ---Distance:   dCru = dSiri - dAcc - dDec = 8.58 LY - .38 LY - .38 LY = 7.82 LY ---Time: tCru =  dCru / vCru = 7.92 LY / (.644c) = 12.14 years

Total Travel Time to Sirius =  tAcc +  tCru  + tDec = 1.0 yr + 12.14 yr + 1.0 yr = 14.14 yrs

Above assumptions are discussed further in subsequent work.

---

Thought Experiment (TE) lists eight closest stellar systems.

These are our Sun, Sol, plus the seven neighbors within 10 LYs.

OBSERVED: Right Ascension (α in deg.); Declination (δ in deg.); Distance (d in LYs)

d_CEP  = d * cos(α)

3-D Coord. (LYs):  d_CEP = d*cos(δ);  x = d_CEP*cos(α);  y = d_CEP*sin(α);  z = d*sin(δ)

Travel Time (decimal Years): t = t_Acc+ t_Cru + t_Dec = 1 + d_Cru/v_Cru + 1

Stellar RA Dec Dist 3-D Coord. Time Seq. System α δ d x y z t

1 Sol n/a n/a 0 0 0 0 0 (click for more) The Sun is not the center of God's Universe, but it is the center of our Solar System and human existence. The Sun causes the wind to blow,  water to flow,  and grass to grow. With the Sun's energy, we eat our meals, consumate our marriages and live life as we know it. As humans expand to other stars in all different directions, Sol's location will continue to be our center even though other suns might provide our energy.

2 α Centauri 217° -63° 4.37 -1.6 -1.4 -3.8 7.4 (click for more) Alpha Centauri is the brightest star in the southern constellation of Centaurus. High powered binoculars can resolve Alpha Centauri into a binary star system with a third companion dwarf star nearby (designated Alpha Centauri AB-C or α Cen AB-C). Together all three components make a triple star system; observers call it the triple star (or multiple star), α Cen AB-C. Component Sizes and Colors. Sizes and colors of α Cen stars  compared to the Sun. Component stars • α Cen A has 110% of the mass and 152% the luminosity of our Sun, • α Cen B is at 91% of Sol's mass and 50% of its luminosity. A and B take 80 years to orbit about a common center; the distance between them varies from about 30 to 50 AU. Thus, their duplicity is easier to resolve at their widest separation. They average 4.37 light years from the Sun. • α Cen C is by far the smallest at 12.3% Solar mass and 0.17% Sol’s luminosity. C, known as Proxima Centauri, and Alpha Centauri AB form a visual double star, and they are most likely gravitationally bound (about .2 LY apart). Though not visible to the naked eye, Proxima is the closest star to our Sun (4.24 LY away). HUMAN HABITATION. Though closest, the AC system might not be the most suitable destination.  α Cen C undergoes frequent flaring which is no doubt a spectacular show, but there must be considerable risk for habitats orbiting a flaring star.  The AB binary  probably has radiation issues, but we won't know for certain til we actually get there.  If this system has comets and asteroids, then habitats can survive there; however, to thrive there, we need an Earth like planet with Earth like conditions.

3 Barnard's Star 270° 5° 5.96 -0.1 -5.9 0.5 10.1 (click for more) Barnard's Star was discovered by E. E. Barnard in 1916. At approximately 6 LY from Sol, Barnard’s Star is the second closest known stellar system to Sol. (Alpha Centauri system is closest.) Despite its proximity, Barnard's Star is not visible to the unaided eye; however, it is much brighter in infrared. Barnard's Star is a red dwarf of the dim spectral type M4, and it requires a telescope for viewing. Barnard's Star has approximately 17% Sol's mass and 20% Sol's radius.  A red dwarf star. From 7 to 12 billion years of age, some dwarf stars are among the Milky Way's oldest objects and were long assumed to be quiescent. (Our Sol is a fairly young 4.6 billion years old.)  Thus, it was surprising in 1998 when William Cochran, University of Texas, observed an intense stellar flare from Barnard's Star which now has variable star designation: V2500 Ophiuchi. Diane Paulson, now at Goddard Space Flight Center, noted: "given the random flaring activity, the star would be fantastic for amateurs to observe". Red dwarf with an orbiting planet. Controversy: Planets in orbit??? In the 1960’s, Peter van de Kamp, a veteran observer of Barnard's Star since 1938, detected at least one gas giant planet orbiting it. Unfortunately, current research indicates no large planets; however, small terrestrial planets remain a possibility. Barnard's Star is also notable as the notional destination for Project Daedalus, a famous study on the possibility of fast, unmanned travel to nearby star systems using nuclear propulsion. HUMAN HABITATION. Current research into stellar flaring has astrobiological implications: given that the habitable zones of M dwarfs are close to the star, any planets would be strongly influenced by solar flares, winds, and plasma ejection events.

4 Wolf 359 164° 7° 7.78 -7.4 2.1 0.9 12.9  (click for more) Wolf 359 is near the ecliptic,  in the constellation, Leo. At 7.8 LY from Sol, it is one of Sol’s nearest neighbors. Several authors use it for fictional works. Wolf 359’s high proper motion indicates proximity. In 1919, German astronomer Max Wolf, published a catalog of over one thousand high proper motion stars which still bear his name. Number 359 in the list, the star has since been referred to as Wolf 359. Wolf 359 is a relatively young dwarf star less than a billion years of age. At 9% of the Sun's mass, Wolf 359 normally has a very low luminosity, emitting about 0.1% of the Sun's energy. In 1969, it was first noticed that Wolf 359's luminosity varies due to flares.  Since then, Hubble Space Telescope detected 32 flares within a single two hour observation period. Such flares cause strong bursts of X-rays and gamma rays.  Wolf 359 is the red-hued star just above the center. Wolf 359 is just above the low limit for hydrogen fusion through the proton–proton chain reaction: 8% of the Sun's mass. If any smaller, it would be a brown dwarf, a sub-stellar object with no fusion. Wolf 359 has a radius of 110,000 km, 16% of the Sun's radius. By comparison, the equatorial radius of Jupiter (71,492 km) is 65% as large as Wolf 359's. Dwarf stars consume hydrogen at a much lower rate than medium sized stars (for example, like Sol, our sun). Thus, Wolf 359 can theoretically remain a main-sequence star for eight trillion years.  HUMAN HABITATION. Hubble Space Telescope reveals no large companions; thus, there is likely no gas giant for a source of He3. While there could be a terrestrial planet within one AU of Wolf 359, the absence of excess infrared emission indicates no debris disk. Thus, there could be a dearth of comets and asteroids for sources of water, building materials and sources of He3.  To find out for sure, we have to go there.

5 Lalande 21185 166° 36° 8.29 -6.5 1.6 4.9 13.7  (click for more) Lalande 21185 is a red dwarf star in Ursa Major. Though very close to Sol (8.3 LYs), viewing still requires a small telescope. At 46% of Sol’s radius, it is much cooler than the Sun at 3,383° K. Alternate designations include: BD+36 2147, Gliese 411, and HD 95735. In 1801, Lalande 21185 was first mentioned in the star catalog, Histoire Céleste Française, by French astronomer Jérôme Lalande of the Paris Observatory. With over 47,000 stars, the 1847 edition added sequence numbers. This star happened to be number 21,185; and for decades, it attracted no more attention then the other entries. Today, Lalande 21185 is well known as Sol’s fourth closest neighbor. Current catalogs classify it as a flare star. Observations confirm X-ray emissions; however, the flares of Lalande 21185 are rather mild when compared to other flare stars.Star’s namesake, Joseph-Jérôme Lefrançais de Lalande, authored several astronomy textbooks and was well known during his lifetime. However, his activities extended well beyond astronomy. For example, to reduce public fear of spiders, he swallowed several of them during a demonstration. He hid royalist friends in the Paris Observatory during the French Revolution, and he made a balloon ascent at age 67. Ironically, Lalande missed a great astronomic opportunity, the discovery of Neptune. In 1795 (14 years after W. Herschel discovered Uranus), Lalande (or his staff) recorded Neptune as a star on two successive nights with different positions.  This anomaly should have alerted the observer(s). However, it went unnoticed and Neptune, the planet, was discovered 51 years later. Planets in the Lalande 21185 System? In 1951, Peter van de Kamp thought that he detected a planetary system using photographic plates taken with the 24-in refractor telescope at Swarthmore College's Sproul Observatory. (See astrometric detection.) In 1960, van de Kamp’s student, Sarah Lippincott, repeated her mentor’s results with more observations with different parameters. Unfortunately, involved photographic plates were later shown to be flawed. Thus, claims of planetary companions were refuted in 1974 with astrometric measurements by George Gatewood of the Allegheny Observatory.  HUMAN HABITATION. Negative results for planet searches thus far do not entirely preclude a planetary system, but they do set an upper bound on the size of any planets that might be present. With current technology, the detection limit for this star system is a little less than  Jupiter sized planets. New terrestrial and space-based instruments will certainly lower this limit further and possibly detect any small planets.

6 Sirius 101° -17° 8.58 -1.6 8.2 -2.6 14.4 (click for more) Artistic conception of Sirius system shows  Sirius-A to far outshiine Sirius B in visible light. Sirius is by far the brightest star in the night sky, almost twice as bright as the next brightest star (Canopus). Sirius’s brightness is due to its size and proximity. At 8.6 LY, it is one of Earth's nearest neighbors. While dimmer than Luna (our Moon), Venus, or Jupiter; Sirius sometimes outshines planets: Mercury and Mars. Under the right conditions, Sirius can even be observed in daylight with the naked eye.  To paddle their outriggers around the vast Pacific Ocean, Polynesians used this prominent star to navigate with extreme precision. Modern  telescopes (or large binoculars) resolve Sirius into two stars, a binary star system. • Sirius A is a white main sequence star about twice the size of Sol. • Sirius B is a faint white dwarf but a prolific emitter of X-rays. During their 49 year orbit, distance between A and B varies from 8.1 to 31.5 AU.  Chandra X-ray Observatory shows Sirius B as far brighter in X-ray spectrum. Credit: NASA/SAO/CXC HUMAN HABITATION. At 8.6 LYs, Sirius is Sol’s fifth closest stellar system and a definite candidate for interstellar travel. Plentiful x-rays from Sirius B might make long term habitation less likely; but other measurements indicate some hospitality from our neighbor. Sirius system emits a higher than expected level of infrared radiation (measured by IRAS space-based observatory) which indicates dust in the Sirius System. Such IR measurements are unusual for a binary star; however, presence of dust leads us to consider possibility of larger objects such as comets and asteroids. Thus, the presence of liquids (comets) and raw materials (asteroids) would make the Sirius system a more likely candidate as a stopover location for subsequent travel.

7 Luyten 726-8 25° -18° 8.79 7.5 3.5 -2.7 14.4 (click for more) Luyten 726-8 (also "Gliese 65") is a binary star system about 8.8 light years from Earth in the constellation Cetus. Luyten 726-8B also has variable star designation UV Ceti, being the archetype for the class of flare stars. is thus the sixth-closest star system to Earth. Binary Star In 1948, Willem Jacob Luyten discovered Luyten 726-8 while cataloging high proper motion stars. He noted its exceptionally high proper motion of 3.37 arc seconds per year and cataloged it as Luyten 726-8. Both stars has nearly equal brightness. Their orbit has a period of 26.5 years and their separation ranges from 2.1 to 8.8 AU. Luyten 726-8A has variable star designation BL It is a red dwarf and is also a flare star, a UV Ceti variable type. Luyten 726-8B After the discovery of Luyten 726-8A, the slightly brighter companion star Luyten 726-8B was discovered. B is also variable and now has the variable star designation: UV Ceti. UV Ceti  is the most prominent example of a flare star; thus, similar flare stars are now classified as UV Ceti type variable stars. This star goes through fairly extreme changes of brightness: for instance, in 1952, its brightness increased by 75 times in only 20 seconds. UV Ceti is a red dwarf of spectral type M6.0e. Close encountersIn approximately 31,500 years, Luyten 726-8 will encounter Epsilon Eridani at the minimal distance of about 0.93 ly. Luyten 726-8 can penetrate a conjectured Oort cloud about Epsilon Eridani, which may gravitationally perturb some long-period comets. The duration of mutual transit of two star systems within 1 ly from each other is about 4,600 years.[7] Luyten 726-8 is a possible member of the Hyades Stream.

8 Ross 154 283° -23° 9.68 1.9 -8.7 -3.8 15.9 (click for more)  Ross 154 (V1216 Sgr) is a red dwarf star approximately 3.0 pc or 9.68 light years from the Sun. It is the nearest star in the southern constellation Sagittarius, and one of the closest to the Sun. Its nearest neighbor is Barnard's star, located 1.66 pc (5.41 ly) away. This star was first catalogued by Frank Elmore Ross in 1925, and formed part of his fourth list of new variable stars.[9] It was found to be a UV Ceti-type flare star, with a mean time between major flares of about two days.[10] Typically, the star will increase by 3–4 magnitudes during a flare.[11] However, at 11th magnitude, this star is much too faint to be viewed with the unaided eye and requires at least a 65 mm telescope aperture to be seen under ideal conditions.[12] Ross 154 has an estimated 17% of the Sun's mass[5] and is only 24% of the Sun's radius.[6] Based on the relatively high projected rotation, this is probably a young star with an estimated age of less than a billion years. The abundance of elements heavier than helium is about half that of the Sun. The strength of the star's magnetic field is an estimated 2.6±0.3 kG. This star is an X-ray source and it has been detected by several X-ray observatories. X-ray flare emission from Ross 154 has been observed by Chandra observatory.[8] The space velocity components of this star are U = –12.2, V = -1.0 and W = -7.2 km/s.[13] It has not been identified as a member of a specific stellar moving group.[14] It is orbiting through the Milky Way galaxy at a distance from the core that varies from 8.478–9.400 kpc and an orbital eccentricity of 0.052.[15] Based on its low velocity relative to the Sun, this is believed to be a young disk (Population I) star.[16] It is predicted that this star will make its closest approach to the Sun in 150,000 years, when it comes within 1.88 ± 0.08 pc (6.13 ly).[17] No low-mass companions have been discovered in orbit around this star.[18] See alsoFrank Elmore Ross List of nearest stars Ross 154 in fiction

Even the closest stellar destinations are very distant in all different directions.